【python】python实现杨辉三角的三种方法
文章目录
- 1.杨辉三角介绍:
- 2.方法一:迭代
- 3.方法二:生成器
- 4.方法三:递归
1.杨辉三角介绍:
杨辉三角是一种数学图形,由数字排列成类似三角形的形状。它的每个数值等于它上方两个数值之和。这个三角形的形状可以用一个二维表格来表示,其中每个位置上的数值都是通过前一行的数值计算得到的。在这个三角形中,第一行只有一个数值1,第二行有两个数值1,第三行有三个数值1,以此类推。从第四行开始,除了首尾的1之外,中间的数值是上一行对应位置的两个数值之和。 下面是一些杨辉三角常见的特点和应用:
- 对称性:杨辉三角以中心轴为对称轴,每行的对称位置上的数值相等。
- 组合数性质:杨辉三角中的数值可以表示为组合数,例如,第n行第k个数值表示为C(n-1, k-1),即从n-1个物体中选取k-1个的组合数。
- 幂和性质:杨辉三角的每一行的数值之和都是2的幂,例如,第n行的数值之和为2^(n-1)。
- 整数序列性质:杨辉三角的每一行对应着一个整数序列,如斐波那契数列、自然数序列等。
杨辉三角不仅仅是一个有趣的数学图形,还有许多实际应用。它在组合数学、概率论、代数等领域都有重要的应用,例如计算二项式的展开系数、解决概率分布问题、生成多项式系数等。
通过编程语言(如Python),可以实现杨辉三角并以可视化的方式显示出来。这样的程序可以逐行计算并输出杨辉三角的数值,从而更好地展示其规律和特点,并可用于相关计算和问题求解。
2.方法一:迭代
代码试例:
def triangle_1(x):""":param x: 需要生成的杨辉三角行数:return:"""triangle = [[1], [1, 1]] # 初始化杨辉三角n = 3 # 从第三行开始计数,逐行添加while n <= x:for i in range(0, n-1):if i == 0:# 添加初始列表[1,1],杨辉三角每行的首位和末位必为1triangle.append([1, 1])else:# 逐位计算,并插入初始列表中triangle[n-1].insert(i, triangle[n - 2][i] + triangle[n - 2][i - 1])n += 1return triangle
x = 11
triangle = triangle_1(x)# 遍历结果,逐行打印
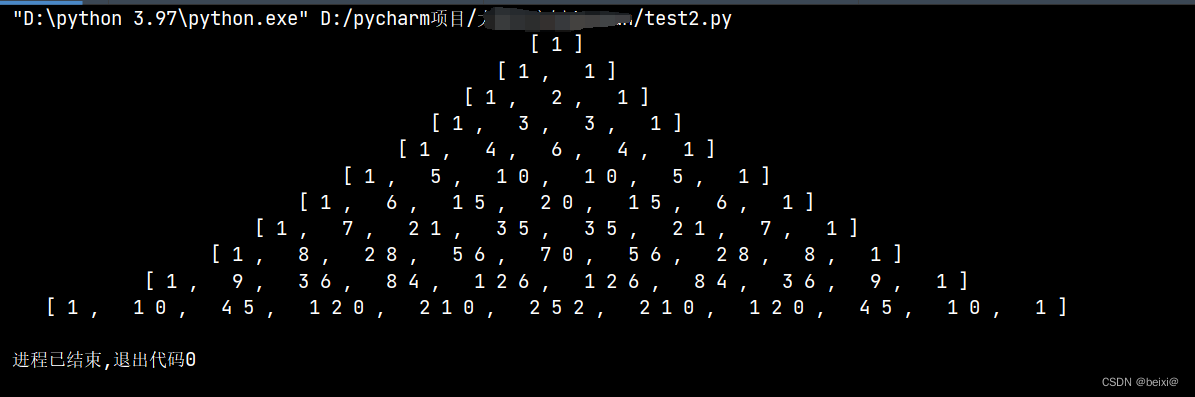
for i in range(x):print(' '.join(str(triangle[i])).center(100)) # 转为str,居中显示
运行结果:
3.方法二:生成器
代码试例:
def triangle_2(n):""":param n: 需要生成的杨辉三角行数:return: """triangle = [1] # 初始化杨辉三角for i in range(n):yield triangletriangle.append(0) # 在最后一位加个0,用于计算下一行triangle = [triangle[i] + triangle[i - 1] for i in range(len(triangle))]
# 从生成器取值
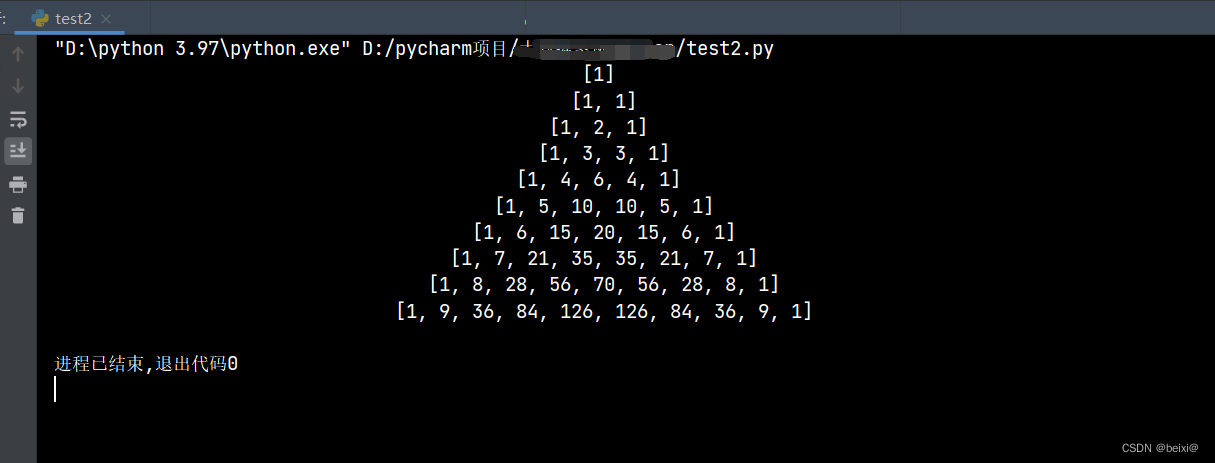
for i in triangle_2(10):print(''.join(str(i)).center(100)) # 格式化输出
运行结果:
4.方法三:递归
杨辉三角特性:
【1,1】=【0,1】+【1,0】
【1,2,1】=【0,1,1】+【1,1,0】
【1,3,3,1】=【0,1,2,1】+【1,2,1,0】
【1,4,6,4,1】=【0,1,3,3,1】+【1,3,3,1,0】
第n行等于第n-1行分别首尾补0,然后按位相加
试例代码:
def triangle_3(n):""":param n:需要生成的杨辉三角行数:return:"""triangle = [1] # 初始化杨辉三角if n == 0:return trianglereturn [x+y for x, y in zip([0] + triangle_4(n - 1), triangle_4(n - 1) + [0])]
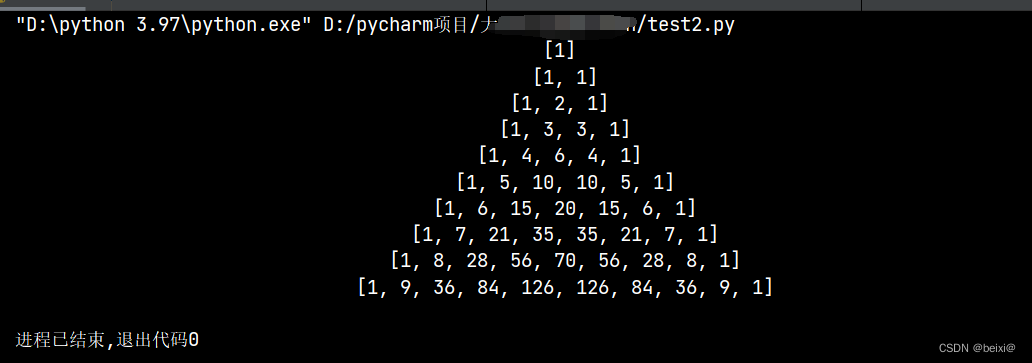
for i in range(10):print(''.join(str(triangle_4(i))).center(100))
运行结果:
到此这篇关于python实现杨辉三角的三种方法代码实例的文章就介绍到这了,如果本篇文章对你有帮助,记得点赞收藏+关注哦~

