【数据结构--八大排序】之堆排序

💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃个人主页 :阿然成长日记 👈点击可跳转
📆 个人专栏: 🔹数据结构与算法🔹C语言进阶
🚩 不能则学,不知则问,耻于问人,决无长进
🍭 🍯 🍎 🍏 🍊 🍋 🍒 🍇 🍉 🍓 🍑 🍈 🍌 🍐 🍍
文章目录
- 堆排序
- 一、🌱排降序
- 1.思路:
- 2.代码实现:
- 3.测试结果
- 4.总代码
- 二、🌸排升序
- 1.思路:
- 2.代码实现:
- 3.测试结果:
- 4.总代码
- 三、堆排序的时间复杂度

堆排序
一、🌱排降序
口诀:排降序,建小堆
1.思路:
(1)首先使用从下到上的方法建立小堆;如下图
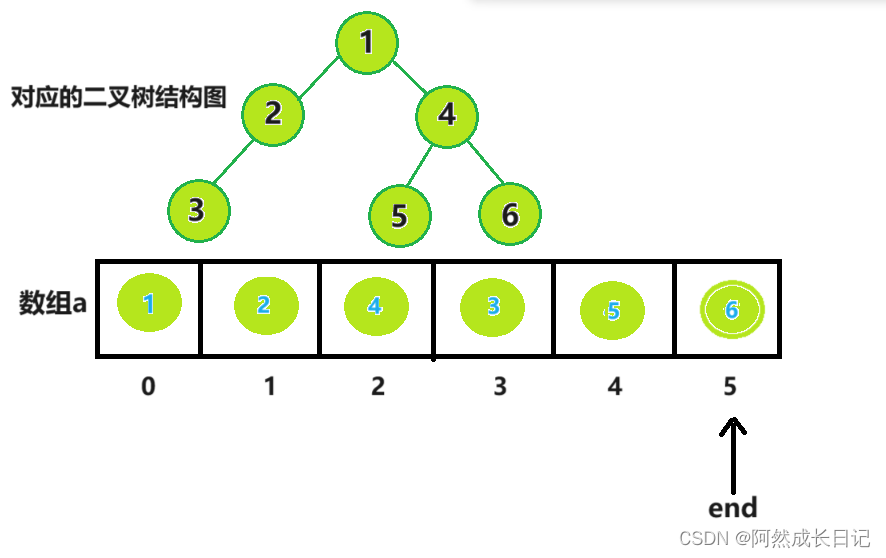
(2)堆顶与最后一个节点交换,由于是小堆,堆顶是最小值。交换后,就选出了最小值并将其放到数组的组后位置,
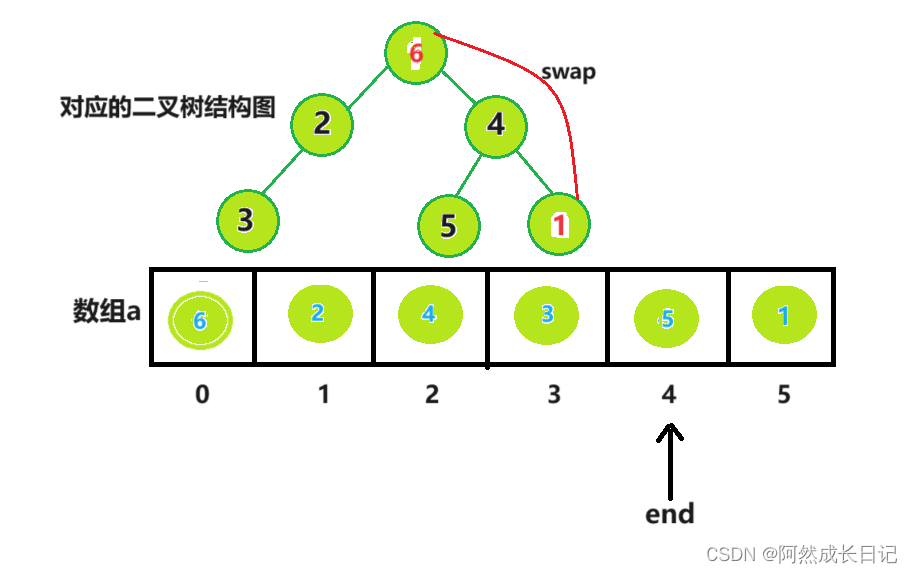
(3).将堆的长度减1【end–】(数组长度减1)。
(4).在对剩下的堆进行基于小堆的向下调整,从而将第二小的数调整到了堆顶。

重复步骤2.3.4,end一直减到0;
4.最后,这个原本存储小堆的数组,就变成了一个从小到大的降序数组。
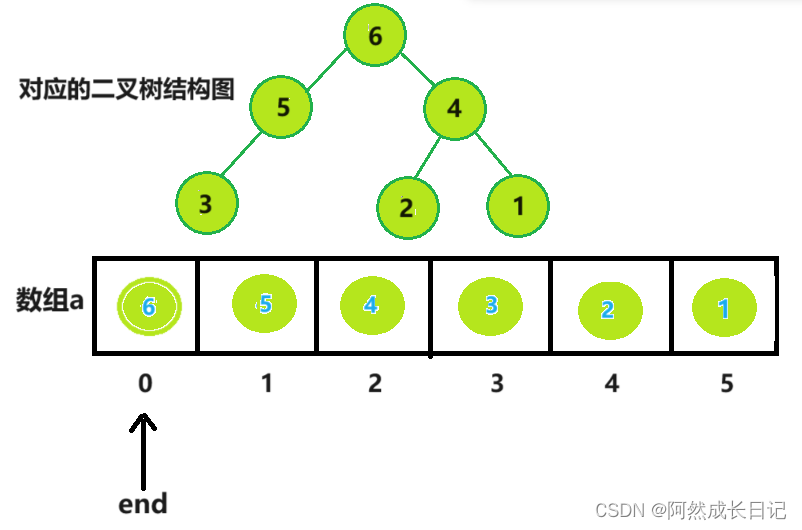
2.代码实现:
1.交换
//交换
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
2.修改AdjustDown(a, end, 0);为调小堆
基于小堆的向下调整
```cvoid AdjustDownxiao(int* a, int n, int parent)
{int child = parent * 2 + 1;//一直交换到数的最后,也就是数组的最后一个位置while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{return;}}
}
3.排降序
void HeapSortDES(int* a, int n)
{//建立小堆for (int i = (n-1-1)/2; i >= 0; i--){AdjustDownxiao(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);//每次调整从根0到end,end每次会减1。AdjustDownxiao(a, end, 0);--end;}
}3.测试结果

4.总代码
//交换
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
//基于小堆的向下调整
void AdjustDownxiao(int* a, int n, int parent)
{int child = parent * 2 + 1;//一直交换到数的最后,也就是数组的最后一个位置while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{return;}}
}//降序
void HeapSortDES(int* a, int n)
{//建立小堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDownxiao(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);//每次调整从根0到end,end每次会减1。AdjustDownxiao(a, end, 0);end--;}
}二、🌸排升序
口诀:排升序,建大堆
意思是:想要将数组的顺序变成一个升序的,那么可以建立一个大堆存在数组中,在对堆进行调整。即可将数组变成一个升序数组。
1.思路:
首先使用从下到上的方法建立大堆;
1.堆顶与最后一个节点交换,由于是大堆,堆顶是最大值。交换后,就选出了最大值并将其放到数组的组后位置,
2.并将堆的长度减1(数组长度减1)。
3.在对剩下的堆进行基于大堆的向下调整,从而将第二大的数调整到了堆顶。
4.最后,这个原本存储大堆的数组,就变成了一个从小到大的升序数组。
2.代码实现:
1.交换
//交换
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
2.基于大堆的向下调整
//基于大堆的向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;//一直交换到数的最后,也就是数组的最后一个位置while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{return;}}
}
3.排升序
//排升序
void HeapSortASC(int* a, int n)
{//建立大堆for (int i = (n-1-1)/2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){swap(&a[0], &a[end]);//每次调整从根0到end,end每次会减1。AdjustDown(a, end, 0);end--;}
}
3.测试结果:
4.总代码
//交换
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;//一直交换到数的最后,也就是数组的最后一个位置while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{return;}}
}//升序
void HeapSortASC(int* a, int n)
{//建立小堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);//每次调整从根0到end,end每次会减1。AdjustDown(a, end, 0);end--;}
}三、堆排序的时间复杂度
堆排序分两步:1.建堆(使用时间复杂度更低的向下调整建堆)2.排序
向下调整建堆的时间复杂度为O(n);
n-1次删除操作的时间复杂度为O(nlogn);
所以总操作时间复杂度为O(nlogn)
