深度学习-一个简单的深度学习推导
文章目录
- 前言
- 1.sigmod函数
- 2.sigmoid求导
- 3.损失函数loss
- 4.神经网络
- 1.神经网络结构
- 2.公式表示-正向传播
- 3.梯度计算
- 1.Loss 函数
- 2.梯度
- 1.反向传播第2-3层
- 2.反向传播第1-2层
- 3.python代码
- 4.MNIST 数据集
前言
本章主要推导一个简单的两层神经网络。
其中公式入口【入口】
1.sigmod函数
激活函数我们选择sigmod,其如下:
f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
其图形为:
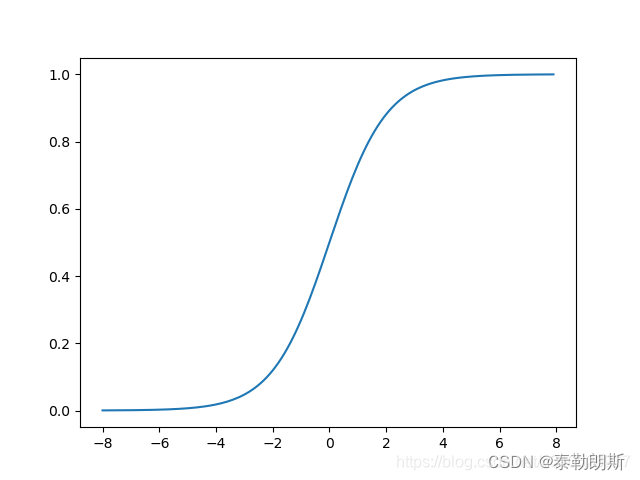
可以用python表示:
def sigmoid(x):return 1.0/(1.0+np.exp(-x))
2.sigmoid求导
先看一个复合函数求导:
如果 y ( u ) = f ( u ) , u ( x ) = g ( x ) , 那么 d y d x = d y d u ∗ d u d x 如果y(u)=f(u),u(x)=g(x), 那么\frac{dy}{dx}=\frac{dy}{du} * \frac{du}{dx} 如果y(u)=f(u),u(x)=g(x),那么dxdy=dudy∗dxdu
那么对于sigmoid函数求导:
f ( x ) = 1 1 + e − x , 那么假设 g ( x ) = 1 + e − x , f ( x ) = 1 g ( x ) f ( x ) ‘ = − 1 g ( x ) 2 ∗ ( − e − x ) = e − x ( 1 + e − x ) 2 = f ( x ) ∗ ( 1 − f ( x ) ) f(x)=\frac{1}{1+e^{-x}},\\ 那么假设g(x)=1+e^{-x}, \\ f(x)=\frac{1}{g(x)}\\ f(x)^`=\frac{-1}{g(x)^2}*{(-e^{-x})}=\frac{e^{-x}}{(1+e^{-x})^{2}}=f(x)*(1-f(x)) f(x)=1+e−x1,那么假设g(x)=1+e−x,f(x)=g(x)1f(x)‘=g(x)2−1∗(−e−x)=(1+e−x)2e−x=f(x)∗(1−f(x))
如果用python表达:
def sigmoid_prime(x):"""sigmoid 函数的导数"""return sigmoid(x)*(1-sigmoid(x))
3.损失函数loss
L o s s = 1 2 ∗ ( y ˘ − y ) 2 Loss=\frac{1}{2}*{(\breve{y}-y)}^2 Loss=21∗(y˘−y)2
它的导数,
L o s s ‘ = y ˘ − y Loss^`=\breve{y}-y Loss‘=y˘−y
4.神经网络
1.神经网络结构
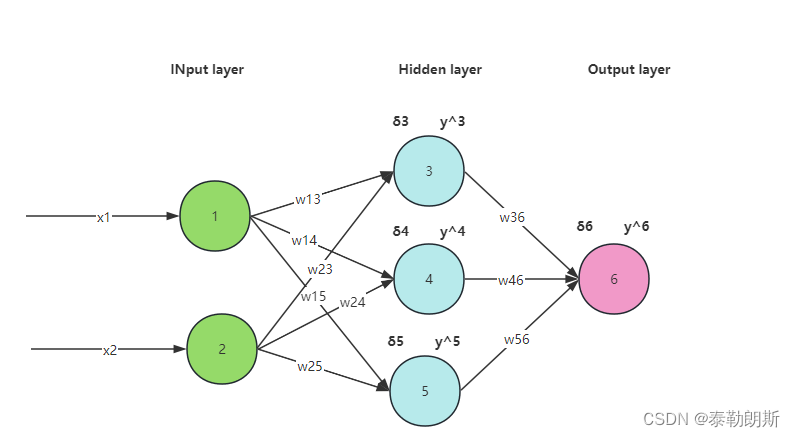
本次我们采用如下神经网络:

2.公式表示-正向传播
w 13 ∗ x 1 + w 23 ∗ x 2 + b 1 = σ 3 , 那么 y 3 ˘ = s i g m o i d ( σ 3 ) w 14 ∗ x 1 + w 24 ∗ x 2 + b 2 = σ 4 , 那么 y 4 ˘ = s i g m o i d ( σ 4 ) w 15 ∗ x 1 + w 25 ∗ x 2 + b 3 = σ 5 , 那么 y 5 ˘ = s i g m o i d ( σ 5 ) 同理可得, w 36 ∗ y 3 ˘ + w 46 ∗ y 4 ˘ + w 56 ∗ y 5 ˘ + b 4 = σ 6 , 那么 y 6 ˘ = s i g m o i d ( σ 6 ) w_{13}*x_1+w_{23}*x_2+b_1=\sigma_3, 那么\breve{y_3}=sigmoid(\sigma_3)\\ w_{14}*x_1+w_{24}*x_2+b_2=\sigma_4, 那么\breve{y_4}=sigmoid(\sigma_4)\\ w_{15}*x_1+w_{25}*x_2+b_3=\sigma_5, 那么\breve{y_5}=sigmoid(\sigma_5)\\ 同理可得,\\ w_{36}*\breve{y_3}+w_{46}*\breve{y_4}+w_{56}*\breve{y_5}+b_4=\sigma_6, 那么\breve{y_6}=sigmoid(\sigma_6)\\ w13∗x1+w23∗x2+b1=σ3,那么y3˘=sigmoid(σ3)w14∗x1+w24∗x2+b2=σ4,那么y4˘=sigmoid(σ4)w15∗x1+w25∗x2+b3=σ5,那么y5˘=sigmoid(σ5)同理可得,w36∗y3˘+w46∗y4˘+w56∗y5˘+b4=σ6,那么y6˘=sigmoid(σ6)
上面的公式我们用矩阵表示:
[ x 1 x 2 ] ⋅ [ w 13 w 14 w 15 w 23 w 24 w 25 ] + [ b 1 b 2 b 3 ] = [ w 13 ∗ x 1 + w 23 ∗ x 2 + b 1 w 14 ∗ x 1 + w 24 ∗ x 2 + b 2 w 15 ∗ x 1 + w 25 ∗ x 2 + b 3 ] = [ σ 3 σ 4 σ 5 ] 代入激活函数, [ s i g m o i d ( σ 3 ) s i g m o i d ( σ 4 ) s i g m o i d ( σ 5 ) ] = [ y 3 ˘ y 4 ˘ y 5 ˘ ] [ y 3 ˘ y 4 ˘ y 5 ˘ ] ⋅ [ w 36 w 46 w 56 ] + [ b 4 ] = [ w 36 ∗ y 3 ˘ + w 46 ∗ y 4 ˘ + w 56 ∗ y 5 ˘ + b 4 ] = σ 6 , s i g m o i d ( σ 6 ) = y ˘ 6 \left[\begin {array}{c} x_1 &x_2 \\ \end{array}\right] \cdot \left[\begin {array}{c} w_{13} &w_{14} & w_{15} \\ w_{23} &w_{24} & w_{25} \\ \end{array}\right]+ \left[\begin {array}{c} b_{1} \\ b_{2} \\ b_{3} \\ \end{array}\right]= \left[\begin {array}{c} w_{13}*x_1+w_{23}*x_2+b_1\\ w_{14}*x_1+w_{24}*x_2+b_2\\ w_{15}*x_1+w_{25}*x_2+b_3\\ \end{array}\right]= \left[\begin {array}{c} \sigma_{3} \\ \sigma_{4} \\ \sigma_{5} \\ \end{array}\right]\\ 代入激活函数,\\ \left[\begin {array}{c} sigmoid(\sigma_3) \\ sigmoid(\sigma_4) \\ sigmoid(\sigma_5) \\ \end{array}\right]= \left[\begin {array}{c} \breve{y_3} \\ \breve{y_4}\\ \breve{y_5} \\ \end{array}\right]\\ \left[\begin {array}{c}\\ \breve{y_3} &\breve{y_4} &\breve{y_5} \\ \end{array}\right] \cdot \left[\begin {array}{c} w_{36} \\ w_{46} \\ w_{56} \\ \end{array}\right]+ \left[\begin {array}{c} b_{4} \\ \end{array}\right]= \left[\begin {array}{c} w_{36}*\breve{y_3}+w_{46}*\breve{y_4}+w_{56}*\breve{y_5}+b_4 \\ \end{array}\right]=\sigma_6\\ ,\\ sigmoid(\sigma_6)=\breve{y}_6 [x1x2]⋅[w13w23w14w24w15w25]+ b1b2b3 = w13∗x1+w23∗x2+b1w14∗x1+w24∗x2+b2w15∗x1+w25∗x2+b3 = σ3σ4σ5 代入激活函数, sigmoid(σ3)sigmoid(σ4)sigmoid(σ5) = y3˘y4˘y5˘ [y3˘y4˘y5˘]⋅ w36w46w56 +[b4]=[w36∗y3˘+w46∗y4˘+w56∗y5˘+b4]=σ6,sigmoid(σ6)=y˘6
3.梯度计算
1.Loss 函数
L o s s = 1 2 ∗ ( y ˘ 6 − y 6 ) 2 Loss=\frac{1}{2}*{(\breve{y}_6-y_6)}^2 Loss=21∗(y˘6−y6)2
2.梯度
1.反向传播第2-3层
[ ∂ l ∂ w 36 ∂ l ∂ w 46 ∂ l ∂ w 56 ] = [ ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ w 36 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ w 46 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ w 56 ] = [ ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ y ˘ 3 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ y ˘ 4 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ y ˘ 5 ] \left[\begin {array}{c} \frac{\partial{l}}{\partial{w_{36}}} \\ \\ \frac{\partial{l}}{\partial{w_{46}}} \\ \\ \frac{\partial{l}}{\partial{w_{56}}} \\ \end{array}\right]= \left[\begin {array}{c} \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{w_{36}}} \\ \\ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{w_{46}}} \\ \\ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{w_{56}}} \\ \end{array}\right]= \left[\begin {array}{c} (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*\breve{y}_3\\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*\breve{y}_4\\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*\breve{y}_5\\ \end{array}\right] \\ ∂w36∂l∂w46∂l∂w56∂l = ∂y˘6∂l∗∂σ6∂y˘6∗∂w36∂σ6∂y˘6∂l∗∂σ6∂y˘6∗∂w46∂σ6∂y˘6∂l∗∂σ6∂y˘6∗∂w56∂σ6 = (y˘6−y6)∗S(σ6)∗(1−S(σ6))∗y˘3(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗y˘4(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗y˘5
上面的式子中 S ( x ) = 1 1 + e − x S(x)=\frac{1}{1+e^{-x}} S(x)=1+e−x1,其中 σ 6 \sigma_6 σ6通过正向传播可以计算出来,具体细节看2式。
根据公式2,我们已经知道 y ˘ 6 \breve{y}_6 y˘6和 y ˘ 3 \breve{y}_3 y˘3的值,所以上面的权重偏导数就能计算出来了。
下面求bias的偏导数, ∂ l ∂ b 4 \frac{\partial{l}}{\partial{b_4}} ∂b4∂l.
∂ l ∂ b 4 = ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ b 4 = ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) \frac{\partial{l}}{\partial{b_4}}= \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{b_4}} = (\breve{y}_6-y_6)* S(\sigma_6)*(1-S(\sigma_6)) ∂b4∂l=∂y˘6∂l∗∂σ6∂y˘6∗∂b4∂σ6=(y˘6−y6)∗S(σ6)∗(1−S(σ6))
2.反向传播第1-2层
权重
[ ∂ l ∂ w 13 ∂ l ∂ w 23 ∂ l ∂ w 14 ∂ l ∂ w 24 ∂ l ∂ w 15 ∂ l ∂ w 25 ] = [ ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 3 ∗ ∂ y ˘ 3 ∂ σ 3 ∗ ∂ σ 3 ∂ w 13 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 3 ∗ ∂ y ˘ 3 ∂ σ 3 ∗ ∂ σ 3 ∂ w 23 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 4 ∗ ∂ y ˘ 4 ∂ σ 4 ∗ ∂ σ 4 ∂ w 14 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 4 ∗ ∂ y ˘ 4 ∂ σ 4 ∗ ∂ σ 4 ∂ w 24 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 5 ∗ ∂ y ˘ 5 ∂ σ 5 ∗ ∂ σ 5 ∂ w 15 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 5 ∗ ∂ y ˘ 5 ∂ σ 5 ∗ ∂ σ 5 ∂ w 25 ] = . . [ ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 36 ∗ S ( σ 3 ) ∗ ( 1 − S ( σ 3 ) ) ∗ x 1 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 36 ∗ S ( σ 3 ) ∗ ( 1 − S ( σ 3 ) ) ∗ x 2 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 46 ∗ S ( σ 4 ) ∗ ( 1 − S ( σ 4 ) ) ∗ x 1 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 46 ∗ S ( σ 4 ) ∗ ( 1 − S ( σ 4 ) ) ∗ x 2 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 56 ∗ S ( σ 5 ) ∗ ( 1 − S ( σ 5 ) ) ∗ x 1 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 56 ∗ S ( σ 5 ) ∗ ( 1 − S ( σ 5 ) ) ∗ x 2 ] \left[\begin {array}{c} \frac{\partial{l}}{\partial{w_{13}}} & \frac{\partial{l}}{\partial{w_{23}}} \\ \\ \frac{\partial{l}}{\partial{w_{14}}} & \frac{\partial{l}}{\partial{w_{24}}}\\ \\ \frac{\partial{l}}{\partial{w_{15}}} & \frac{\partial{l}}{\partial{w_{25}}}\\ \end{array}\right]= \left[\begin {array}{c} \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{3}}} * \frac{\partial{\breve{y}_3}}{\partial{\sigma_{3}}} * \frac{\partial{\sigma_3}}{\partial{w_{13}}} & \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{3}}} * \frac{\partial{\breve{y}_3}}{\partial{\sigma_{3}}} * \frac{\partial{\sigma_3}}{\partial{w_{23}}} \\ \\ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{4}}} * \frac{\partial{\breve{y}_4}}{\partial{\sigma_{4}}} * \frac{\partial{\sigma_4}}{\partial{w_{14}}} & \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{4}}} * \frac{\partial{\breve{y}_4}}{\partial{\sigma_{4}}} * \frac{\partial{\sigma_4}}{\partial{w_{24}}} \\ \\ \ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{5}}} * \frac{\partial{\breve{y}_5}}{\partial{\sigma_{5}}} * \frac{\partial{\sigma_5}}{\partial{w_{15}}} & \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{5}}} * \frac{\partial{\breve{y}_5}}{\partial{\sigma_{5}}} * \frac{\partial{\sigma_5}}{\partial{w_{25}}} \\ \end{array}\right]=\\ .\\ .\\ \left[\begin {array}{c} (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{36}*S(\sigma_3)*(1-S(\sigma_3))*x_1 & (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{36}*S(\sigma_3)*(1-S(\sigma_3))*x_2 \\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{46}*S(\sigma_4)*(1-S(\sigma_4))*x_1 & (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{46}*S(\sigma_4)*(1-S(\sigma_4))*x_2 \\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{56}*S(\sigma_5)*(1-S(\sigma_5))*x_1 & (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{56}*S(\sigma_5)*(1-S(\sigma_5))*x_2 \end{array}\right] \\ ∂w13∂l∂w14∂l∂w15∂l∂w23∂l∂w24∂l∂w25∂l = ∂y˘6∂l∗∂σ6∂y˘6∗∂y˘3∂σ6∗∂σ3∂y˘3∗∂w13∂σ3∂y˘6∂l∗∂σ6∂y˘6∗∂y˘4∂σ6∗∂σ4∂y˘4∗∂w14∂σ4 ∂y˘6∂l∗∂σ6∂y˘6∗∂y˘5∂σ6∗∂σ5∂y˘5∗∂w15∂σ5∂y˘6∂l∗∂σ6∂y˘6∗∂y˘3∂σ6∗∂σ3∂y˘3∗∂w23∂σ3∂y˘6∂l∗∂σ6∂y˘6∗∂y˘4∂σ6∗∂σ4∂y˘4∗∂w24∂σ4∂y˘6∂l∗∂σ6∂y˘6∗∂y˘5∂σ6∗∂σ5∂y˘5∗∂w25∂σ5 =.. (y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w36∗S(σ3)∗(1−S(σ3))∗x1(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w46∗S(σ4)∗(1−S(σ4))∗x1(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w56∗S(σ5)∗(1−S(σ5))∗x1(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w36∗S(σ3)∗(1−S(σ3))∗x2(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w46∗S(σ4)∗(1−S(σ4))∗x2(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w56∗S(σ5)∗(1−S(σ5))∗x2
偏置
[ ∂ l ∂ b 1 ∂ l ∂ b 2 ∂ l ∂ b 3 ] = [ ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 3 ∗ ∂ y ˘ 3 ∂ σ 3 ∗ ∂ σ 3 ∂ b 1 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 4 ∗ ∂ y ˘ 4 ∂ σ 4 ∗ ∂ σ 4 ∂ b 2 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 5 ∗ ∂ y ˘ 5 ∂ σ 5 ∗ ∂ σ 5 ∂ b 3 ] = . [ ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 36 ∗ S ( σ 3 ) ∗ ( 1 − S ( σ 3 ) ) ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 46 ∗ S ( σ 4 ) ∗ ( 1 − S ( σ 4 ) ) ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 56 ∗ S ( σ 5 ) ∗ ( 1 − S ( σ 5 ) ) ] \left[\begin {array}{c} \frac{\partial{l}}{\partial{b_1}} \\ \\ \frac{\partial{l}}{\partial{b_2}} \\ \\ \frac{\partial{l}}{\partial{b_3}} \\ \end{array}\right]= \left[\begin {array}{c} \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{3}}} * \frac{\partial{\breve{y}_3}}{\partial{\sigma_{3}}} * \frac{\partial{\sigma_3}}{\partial{b_1}} \\ \\ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{4}}} * \frac{\partial{\breve{y}_4}}{\partial{\sigma_{4}}} * \frac{\partial{\sigma_4}}{\partial{b_2}} \\ \\ \ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{5}}} * \frac{\partial{\breve{y}_5}}{\partial{\sigma_{5}}} * \frac{\partial{\sigma_5}}{\partial{b_3}} \\ \end{array}\right]=\\ .\\ \left[\begin {array}{c} (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{36}*S(\sigma_3)*(1-S(\sigma_3)) \\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{46}*S(\sigma_4)*(1-S(\sigma_4)) \\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{56}*S(\sigma_5)*(1-S(\sigma_5)) \end{array}\right] \\ ∂b1∂l∂b2∂l∂b3∂l = ∂y˘6∂l∗∂σ6∂y˘6∗∂y˘3∂σ6∗∂σ3∂y˘3∗∂b1∂σ3∂y˘6∂l∗∂σ6∂y˘6∗∂y˘4∂σ6∗∂σ4∂y˘4∗∂b2∂σ4 ∂y˘6∂l∗∂σ6∂y˘6∗∂y˘5∂σ6∗∂σ5∂y˘5∗∂b3∂σ5 =. (y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w36∗S(σ3)∗(1−S(σ3))(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w46∗S(σ4)∗(1−S(σ4))(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w56∗S(σ5)∗(1−S(σ5))
综上所述,通过反向传播,就可以计算出偏导数了。
3.python代码
根据上面的分析,下面我们写一下python代码,代码就很简单了
import numpy as np
import random
import os"""核心就是如何布局biases和weights这两个矩阵"""class Network(object):"""列表sizes包含对应层的神经元数目,如果列表是[2,3,1],那么就是指一个三层神经网络,第一层有2个神经元,第二层有3个神经元,第三次有1个神经元."""def __init__(self, sizes):"""这里num_layers是3"""self.num_layers=len(sizes)self.sizes=sizes"""随机初始化偏差,初始化后如下[array([[-1.17963885],[ 0.41953645],[-0.88551629]]), array([[0.20600121]])]特别注意这里是3x1的一个矩阵"""self.biases=[np.random.randn(y,1) for y in sizes[1:]]"""随机初始化权重[array([[-0.25009885, -0.33699188],[-0.53513364, -1.57623694],[ 1.89456316, 0.66985265]]), array([[-0.18411963, -0.08143799, 0.53533203]])]上面两个矩阵是3x2,1x3"""self.weights=[np.random.randn(y,x) for x,y in zip(sizes[:-1],sizes[1:])]def feedforward(self,x):"""输入可以认为是一个2x1的向量,因为列才是向量比如下面的点积,[3x2]*[2*1] + [3*1] = [3*1]"""a=np.array(x).reshape(len(x),1)for b, w in zip(self.biases,self.weights):a=sigmoid(np.dot(w,a)+b)return adef SGD(self,training_data,epochs,mini_batch_size,eta,test_data=None):"""使用小批量随机梯度下降算法训练神经网络,使用training_data是由训练输入和目标输出的元组(x,y)组成。"""if(test_data):n_test=len(test_data)n=len(training_data)for j in range(epochs):random.shuffle(training_data)mini_batchs=[training_data[k:k+mini_batch_size]for k in range(0,n,mini_batch_size)]for mini_batch in mini_batchs:self.update_mini_batch(mini_batch,eta)if test_data:print("Epoch {0}:{1}/{2}".format(j,self.evaluate(test_data),n_test))else:print("Epoch {0} complete.".format(j))def update_mini_batch(self,mini_batch,eta):"""使用小批量应用梯度下降算法和反向传播算法来更新神经网络的权重和偏置。mini_batch是又若干元组组成的(x,y)组成的列表,eta为学习率。其中x为batch * 2 * 1"""nabla_b=[np.zeros(b.shape) for b in self.biases]nablea_w=[np.zeros(w.shape) for w in self.weights]for x,y in mini_batch:"""计算梯度"""delta_nabla_b,delta_nable_w=self.backprob(x,y)nabla_b=[nb+dnb for nb,dnb in zip(nabla_b,delta_nabla_b)]nablea_w=[nw+dnw for nw,dnw in zip(nablea_w,nablea_w)]self.weights=[w-(eta/len(mini_batch)) * nw for w,nw in zip(self.weights,nablea_w)]self.biases=[b-(eta/len(mini_batch)) * nb for b,nb in zip(self.biases,nabla_b)]def backprob(self,a,b):nabla_b=[np.zeros(b.shape) for b in self.biases]nabla_w=[np.zeros(w.shape) for w in self.weights]x=np.array(a).reshape(len(a),1)y=np.array(b).reshape(len(b),1)activation=xactivations=[x]zs=[]"""正向传播biases 是[3x1,1x1]weights是[3x2,1x3]第1-2层的计算[3x2] * [2*1] + [3x1] = [3x1]第2-3层的计算[1x3] * [3x1] + [1x1] = [1x1] """for b,w in zip(self.biases,self.weights):z=np.dot(w,activation) + b"""未激活"""zs.append(z)"""激活函数"""activation=sigmoid(z)activations.append(activation)"""反向传播,计算最后2层的梯度"""delta=self.cost_derivative(activations[-1],y) * sigmoid_prime(zs[-1])nabla_b[-1]=deltanabla_w[-1]=np.dot(delta,activations[-2].transpose())"""反向传播,计算其余层梯度"""for l in range(2,self.num_layers):z=zs[-l]sp=sigmoid_prime(z)delta=np.dot(self.weights[-l+1].transpose(),delta) * spnabla_b[-l] =deltanabla_w[-l] = np.dot(delta,activations[-l-1].transpose())return (nabla_b,nabla_w)def evaluate(self,test_data):"""argmax返回的是a中元素最大值所对应的索引值"""# test_results=[(np.argmax(self.feedforward(x),y)) for x,y in test_data] test_results=[(self.feedforward(x),y) for x,y in test_data] return sum(int(compare_float(x,y,0.001)) for x,y in test_results)def cost_derivative(self,output_activations,y):"""loss函数的导数 loss=1/2 * (y^ - y)^2"""return (output_activations)def compare_float(a, b, precision):if abs(a - b) <= precision:return 1return 0def sigmoid(x):return 1.0/(1.0+np.exp(-x))"""sigmoid的导数"""
def sigmoid_prime(x):return sigmoid(x)*(1-sigmoid(x))4.MNIST 数据集
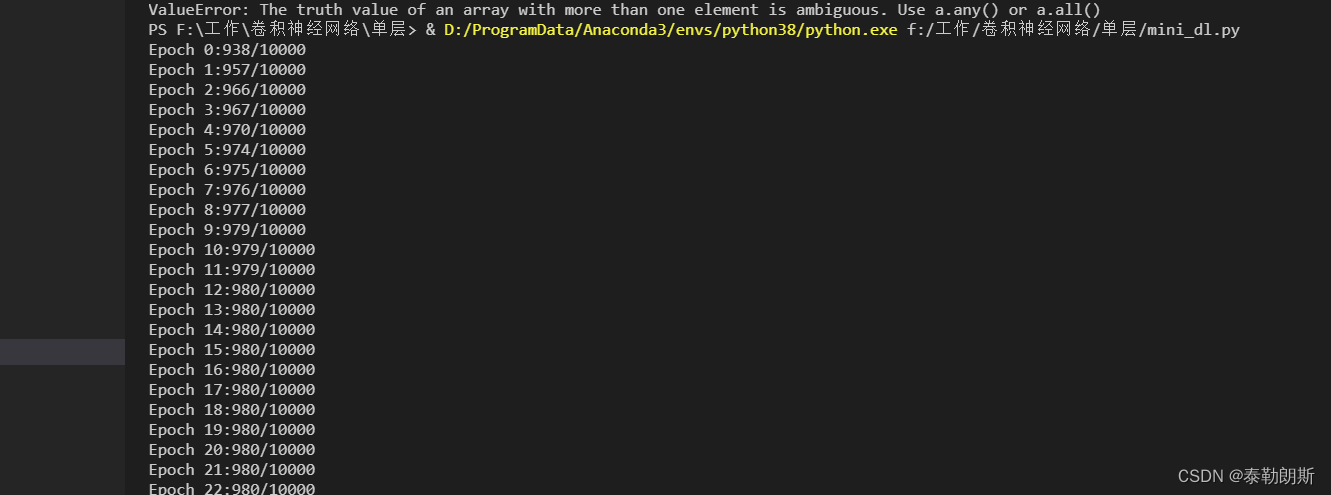
写好代码后我们用测试集测试一下
链接: https://pan.baidu.com/s/1gSeRPwDODK4IeZLVsmPBfQ?pwd=6zcp
提取码: 6zcp
import MNIST.mnist as mnistif __name__=="__main__":dataset=mnist.load_mnist()training_data=dataset[0][0]training_label=dataset[0][1]test_data=dataset[1][0]test_lable=dataset[1][1]net = Network([784,30,1])td=[(np.array(x.copy()),[np.array(y.copy())]) for (x,y) in zip(training_data,training_label)]tt_d=[(np.array(x.copy()),[np.array(y.copy())]) for (x,y) in zip(test_data,test_lable)]net.SGD(td,30,10,3.0,tt_d)
结果如下,可以看到最后精度稳定在98%,还可以: