[牛客复盘] 牛客周赛round13 20230924
[牛客复盘] 牛客周赛round13 20230924
- 总结
- 矩阵转置置
- 2. 思路分析
- 3. 代码实现
- 小红买基金
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 小红的密码修改
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 小红的转账设置方式
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 小红打boss
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
总结
- 竟然三题下班了,哭了。
- A模拟
- B乘法原理
- C分类讨论乘法原理
- D 最短路方案数,乘法原理
- E 贪心
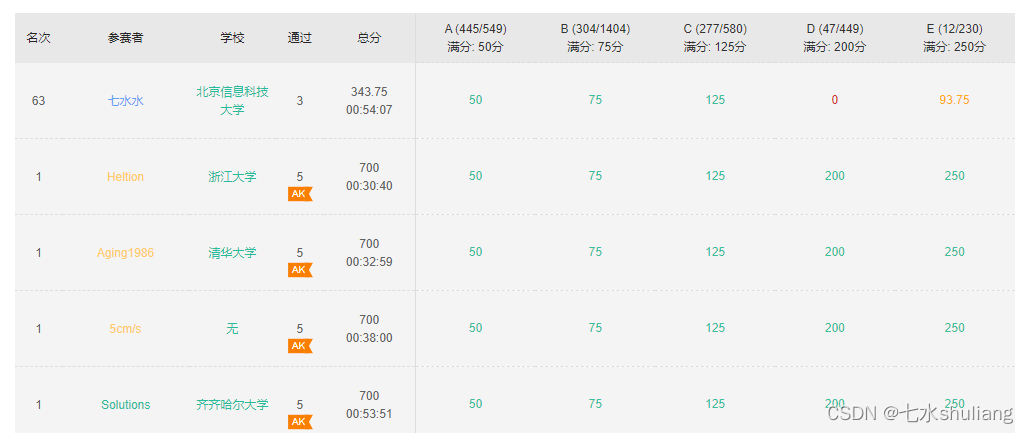
矩阵转置置
链接: [矩阵转置置
2. 思路分析
- 按题意模拟,翻转两次。
3. 代码实现
def solve():n, = RI()g = []for _ in range(n):g.append(RILST())for i,row in enumerate(g):g[i] = row[::-1]for j in range(n):l,r = 0,n-1while l < r:g[l][j],g[r][j] = g[r][j],g[l][j]l += 1r -= 1for row in g:print(*row)
小红买基金
链接: 小红买基金
1. 题目描述
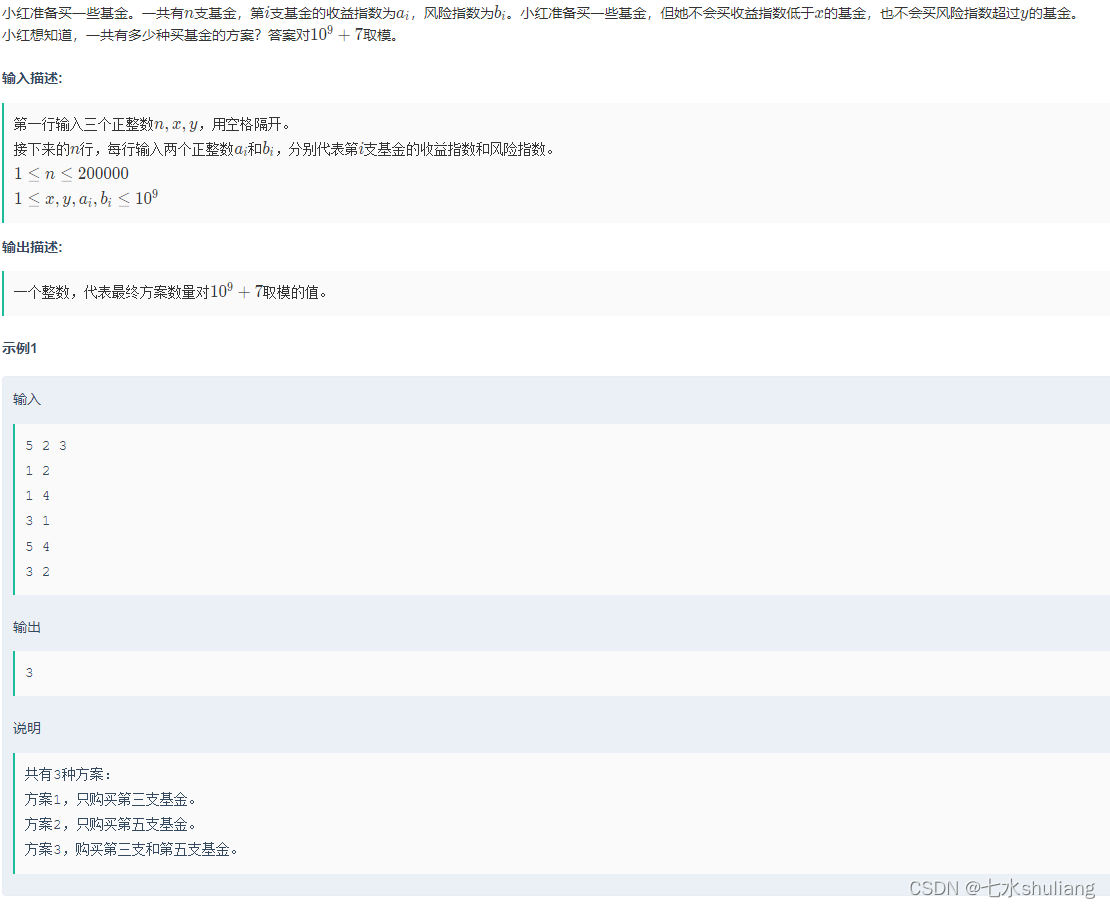
2. 思路分析
- 每个符合要求的基金都可以选择买或不买,最后减去买0枝的方案。
3. 代码实现
def solve():n, x, y = RI()p = 0for _ in range(n):a, b = RI()if a >= x and b <= y:p += 1print((pow(2, p, MOD) - 1) % MOD)
小红的密码修改
链接: 小红的密码修改
1. 题目描述
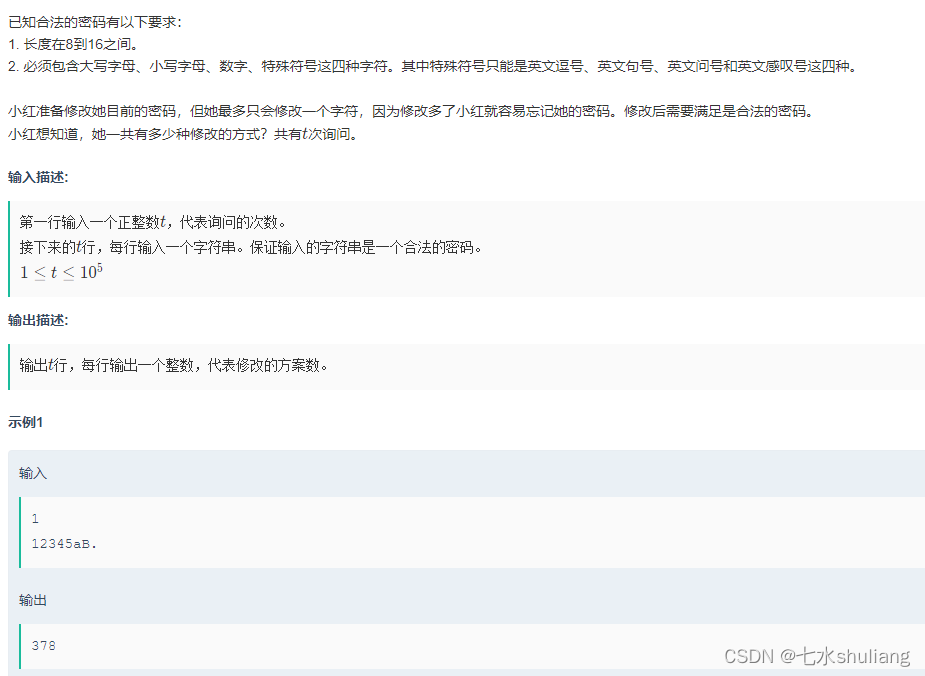
2. 思路分析
- 由于本身输入是合法的,那么对于每个字符可以修改成同类字符;如果本类字符有超过1个,那么还可以修改成其它类字符。
3. 代码实现
def solve():s, = RS()n = len(s)up = low = dig = sp = 0for c in s:if c.isdigit():dig += 1elif c.islower():low += 1elif c.isupper():up += 1else:sp += 1ans = 0for c in s:if c.isdigit():if dig == 1:ans += 9else:ans += 9 + 26 + 26 + 4elif c.islower():if low == 1:ans += 25else:ans += 10 + 25 + 26 + 4elif c.isupper():if up == 1:ans += 25else:ans += 10 + 25 + 26 + 4else:if sp == 1:ans += 3else:ans += 10 + 26 + 26 + 3ans %= MODprint(ans)
小红的转账设置方式
链接: 小红的转账设置方式
1. 题目描述

2. 思路分析
题目给出了n个点和m条无向边,要求调整为有向边,且使得所有点到1的最短路最短。问有几种方案。
- 先无脑求出最短路,然后考虑每条边的调整方案。
- 不在最短路上的边,两个方向都可以,乘2即可。注意不要算两次。
- 在最短路上的边,连接u,v,那么一定有dis[u]+1==dis[v],那么我们从v的角度考虑。
- u可能对应着p条边(点),都可以使u的最短路最短,那么保留一条或多条都可以。
- 一共有2^p-1种方案。
3. 代码实现
def solve():n, m = RI()g = [[] for _ in range(n)]for _ in range(m):u, v = RI()g[u - 1].append(v - 1)g[v - 1].append(u - 1)dis = [n] * ndis[0] = 0q = deque([0])while q:u = q.popleft()d = dis[u] + 1for v in g[u]:if d < dis[v]:dis[v] = dq.append(v) ans = 1for u, es in enumerate(g): # 枚举每个点最短路p = 0for v in es:if dis[v] + 1 == dis[u]: # u可以从v来p += 1elif dis[u] + 1 != dis[v] and u > v: # 如果v从u来,则这条边去v里再计算;否则这条边不在最短路上,可以任意方向,但注意只计算一次ans = ans * 2 % MODif p > 1: # u有超过1条边来,那么只有全是反边的情况不可以ans = ans * (pow(2, p, MOD) - 1) % MODprint(sum(dis) % MOD, ans)
小红打boss
链接: 小红打boss
1. 题目描述
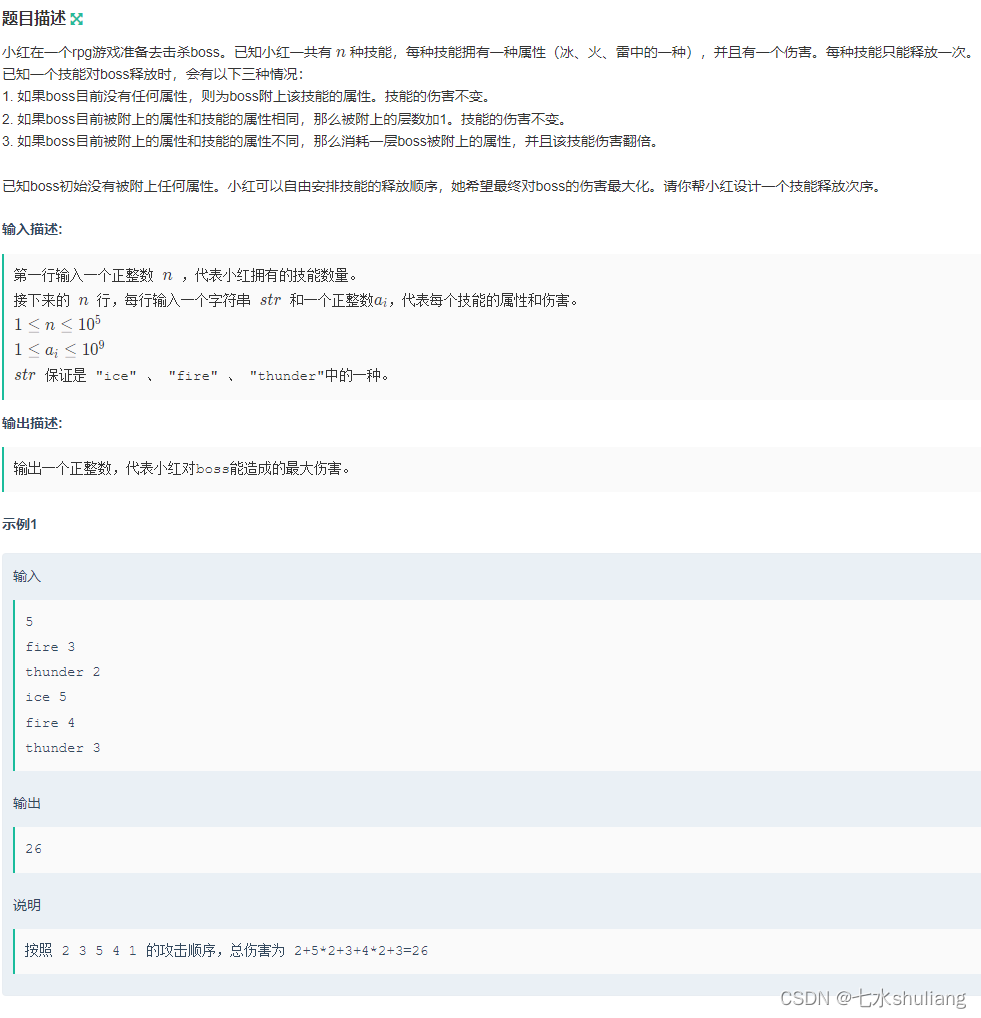
2. 思路分析
- 首先每个技能至少都可以打成单倍伤害。
- 然后考虑哪些技能可以双倍,优先让伤害高的技能双倍。
- 那么可以用一个其它种类的小技能垫一下,然后用大的消耗。
- 显然,最多有n//2个技能可以双倍,但如果最多的那类技能超过了一半,那就不行了:垫的数量不够。
- 因此最多有min(n//2,n-max(cnt))个技能可以双倍。
3. 代码实现
def solve():n, = RI()c = [] # 存所有分数cnt = Counter() # 分别计数for _ in range(n):a, b = RS()c.append(int(b))cnt[a[0]] += 1ans = sum(c)c.sort(reverse=True)ans += sum(c[:min(n // 2, n - max(cnt.values()))]) # 最多取一半;如果有一个太多,只能取不到一半print(ans)
六、参考链接
- 无
