数据结构与算法之时间复杂度和空间复杂度(C语言版)
1. 时间复杂度
1.1 概念
简而言之,算法中的基本操作的执行次数,叫做算法的时间复杂度。也就是说,我这个程序执行了多少次,时间复杂度就是多少。
比如下面这段代码的执行次数:
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}Func1执行的基本操作次数:
F(N) = N^2 + 2*N + 10
在这里两层for循环的次数是N^2,第二个for循环的次数是2*N,while循环的次数是10
所以这个算法中的基本操作次数就是 N^2 + 2*N + 10。
那我们的时间复杂度就是这个吗,其实不是的。实际上我们在计算时间复杂度的时候,我们并不一定要计算精确的执行次数,而只需要大概执行次数。
这又是为什么呢?
当N = 10的时候,F(N) = 130
当 N = 100 的时候,F(N) = 10210
当 N = 1000 的时候,F(N) = 1002010
我们发现当N趋于无穷大的时候,对F(N)影响最大的是N^2,这就跟我们在数学里找极限一样,抓大头,找影响最大的一项,用影响最大的一项来表示我们的时间复杂度
这种表示方法我们称作大O的渐进表示法。
1.2大O的渐进表示法
大O符号(Big O notation):用于描述函数渐进行为的数学符号。
基本执行次数用大O阶方法表示的规则:
1. 如果执行次数中出现加法常数(无论多大,只要是常数),用1来代替。
2. 如果执行次数是多项式,执行次数只保留最高阶项(最高次项)
3. 如果最高阶项存在且不是1,舍去系数。
4.经过1,2,3操作得到的结果就是大O阶表示。
所以我们上面的F(N) = N^2 + 2*N + 10 用大O阶表示就是 O(N^2)。
1.3 最好,平均,最坏情况
有些算法的时间复杂度是存在最好,平均,最坏情况的。
1.最好情况:基本操作次数的最小值
2.平均情况:期望的基本操作次数
3.最坏情况:基本操作次数的最大值
但是在实际中我们都是用最坏情况来表示时间复杂度
1.4 时间复杂度例题
1.4.1 例题1
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}答案:O(N)
基本执行次数是(2 * N + 10),用大O阶表示为O(N)
1.4.2 例题2
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}答案:O(M+N)
基本执行次数是M+N次,由于有两个未知数M和N,所以大O阶表示为O(M+N)
1.4.3 例题3
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}答案:O(1)
基本执行次数是100次,用大O阶表示为O(1)
1.4.4 例题4
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}答案:O(N^2)
基本操作次数是(n-1)+(n-2)+(n-3)+....+3+2+1 = ((n + 1) * n) / 2
最好情况就是遍历一次就排序成功,基本操作次数是n-1,大O阶表示是O(N)
最坏情况就是全部遍历完,基本操作次数是((n + 1) * n) / 2,大O阶表示为O(N^2)
时间复杂度一般看最坏情况,为O(N^2)
大O表示为O(N^2)
1.4.5 例题5
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}答案:O(log N)
这个算法是二分查找
最好情况是查找一次,为O(1)
最坏情况是begin = end 了,只剩了一个元素,我们可以设循环的次数是x,一次循环我们是砍掉了一半的数组元素,那到最后没有元素了,说明n / 2^x = 1
所以x = log n(以2为底)。时间复杂度的大O阶表示就是O(logN)。
我们规定以2为底的对数函数写成 log N
1.4.6 例题6
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}答案:O(N)
基本操作次数:这个函数一共递归了N次,时间复杂度就是O(N)
1.4.7 例题7
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}答案:O(2^N)
基本操作次数:这个函数递归了1+2+4+8+... 是一个不完整的等比数列,在N<3之后不会递归,但是不影响整体的趋势,可以忽略不计,这个等比数列的和是2^n - 1
所以大O阶表示为O(2^n)
2.空间复杂度
2.1概念
空间复杂度指的是临时占用存储空间大小的量度,需要注意的是空间复杂度并不是程序占了多少个字节的空间,因为没有什么太大意义,所以空间复杂度指的是新创建的变量个数
空间复杂度计算规则和时间复杂度基本一致,用大O阶渐渐表示法。
注意⚠️⚠️⚠️:
1. 计算空间复杂度时,一般不需要考虑函数的形式参数。空间复杂度主要关注的是算法执行过程中所占用的额外空间,而函数的形式参数在函数调用时会被压入调用栈中,属于函数调用过程中的内存分配,并不计入空间复杂度的计算。
2. 递归算法在每次递归调用时需要维护函数调用栈,而函数调用栈会占用额外的内存空间,所以其空间复杂度为递归所使用的堆栈空间的大小。
2.2 空间复杂度例题
2.2.1 例题1
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i) {if (a[i - 1] > a[i]) {Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}这个冒泡排序临时创建的变量分别是 end , exchange 和 i 一共三个,是常数个。
所以空间复杂度用大O阶表示为O(1)
2.2.2 例题2
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}这个算法我们直接看新创建的变量是fibArray这个数组,是动态开辟的一个数组,开辟了n+1个空间,还有个i变量,一共是n+2个变量。
用大O阶表示为O(n)
2.2.3 例题3
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}首先我们要明确的是这是一个函数递归调用
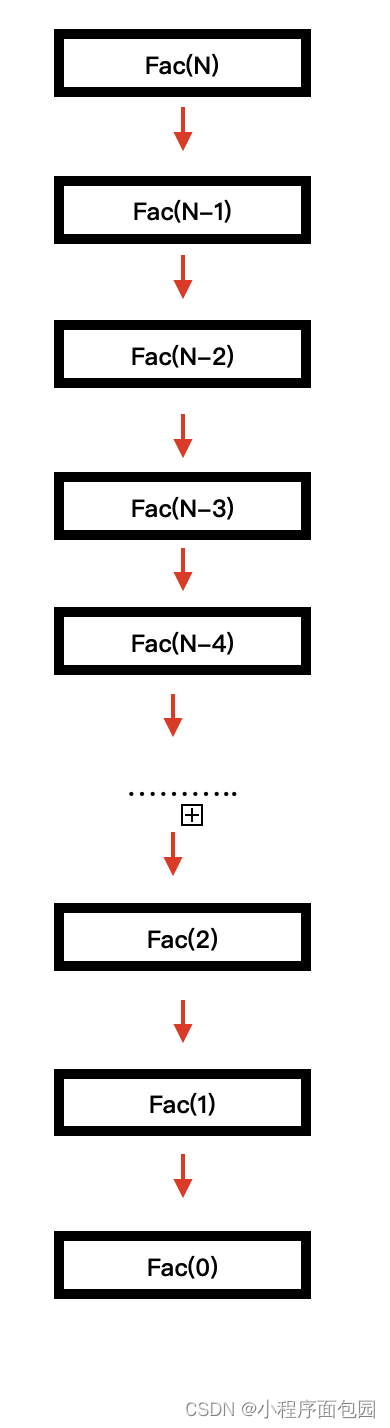
我们函数递归一共要递归N次,共创建新的栈空间N个
所以空间复杂度为O(N)
2.2.4 例题4
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}此时的空间复杂度是多少呢? O(2^N)? 还是O(N)?
我们画图来说明
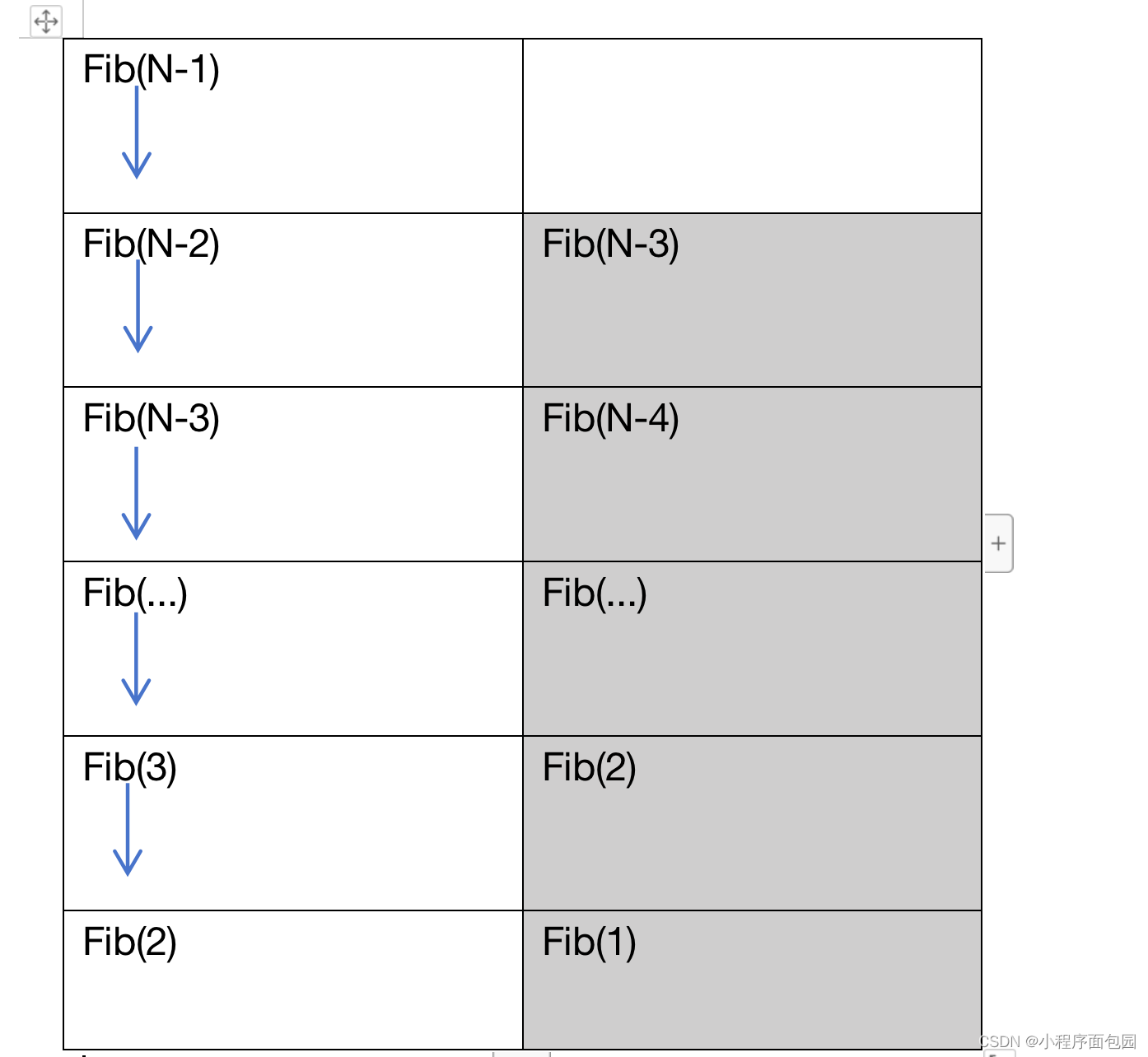
我们来看这个函数的递归调用并不是同时进行的,而是先调用左边的,左边调用完了,最下面Fib(2)往回销毁空间之后才去调用Fib(1),也就是在这个时候才开辟Fib(1)的空间
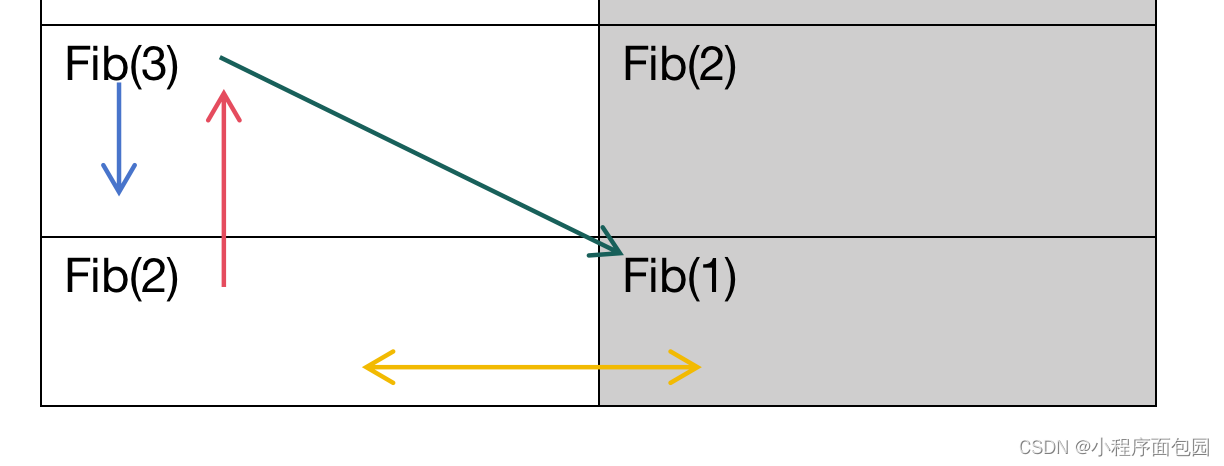
蓝色箭头代表从Fib(3)到Fib(2)先开辟Fib(2)的栈空间,当调用结束的时候,这段空间就要销毁,于是就有了红色的箭头代表销毁Fib(2)的空间,销毁之后我们才开始调用Fib(1),绿色箭头代表调用Fib(1),此时就要开辟Fib(1)的空间,要知道的是我们刚刚销毁一个栈空间,现在又要开辟一个栈空间,所以空间是被重复利用的,也就是黄色的箭头,Fib(1)的空间跟Fib(2)的空间是同一块空间。
所以我们真正开辟的空间只有从Fib(N)到Fib(2)这一段,其他的调用函数,都是在重复利用栈空间的过程。
所以空间复杂度是O(N)
总结:时间是累积的,一去不复返
空间是可以重复利用的。
3.常见复杂度的对比
| 常数阶 | O(1) | 5201314 |
| 线性阶 | O(N) | 3N+1 |
| 平方阶 | O(N^2) | 2N^2 + 3N + 1 |
| 对数阶 | O(logN) | 3log(2)N + 2 |
| NlogN阶 | O(NlogN) | 2N+3Nlog(2)N + 1 |
| 立方阶 | O(N^3) | 3N^3+2N^2+N+1 |
| 指数阶 | O(2^N) | 2^N |
