【2023华为杯B题】DFT类矩阵的整数分解逼近(思路及代码下载)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 详细数学模型及题目、数据
🎉3 参考文献
🌈4 Matlab代码及思路实现
💥1 概述
离散傅里叶变换(Discrete Fourier Transform,DFT)作为一种基本工具广泛应用于工程、科学以及数学领域。例如,通信信号处理中,常用DFT实现信号的正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统的时频域变换(见图1)。另外在信道估计中,也需要用到逆DFT(IDFT)和DFT以便对信道估计结果进行时域降噪(见图2)。
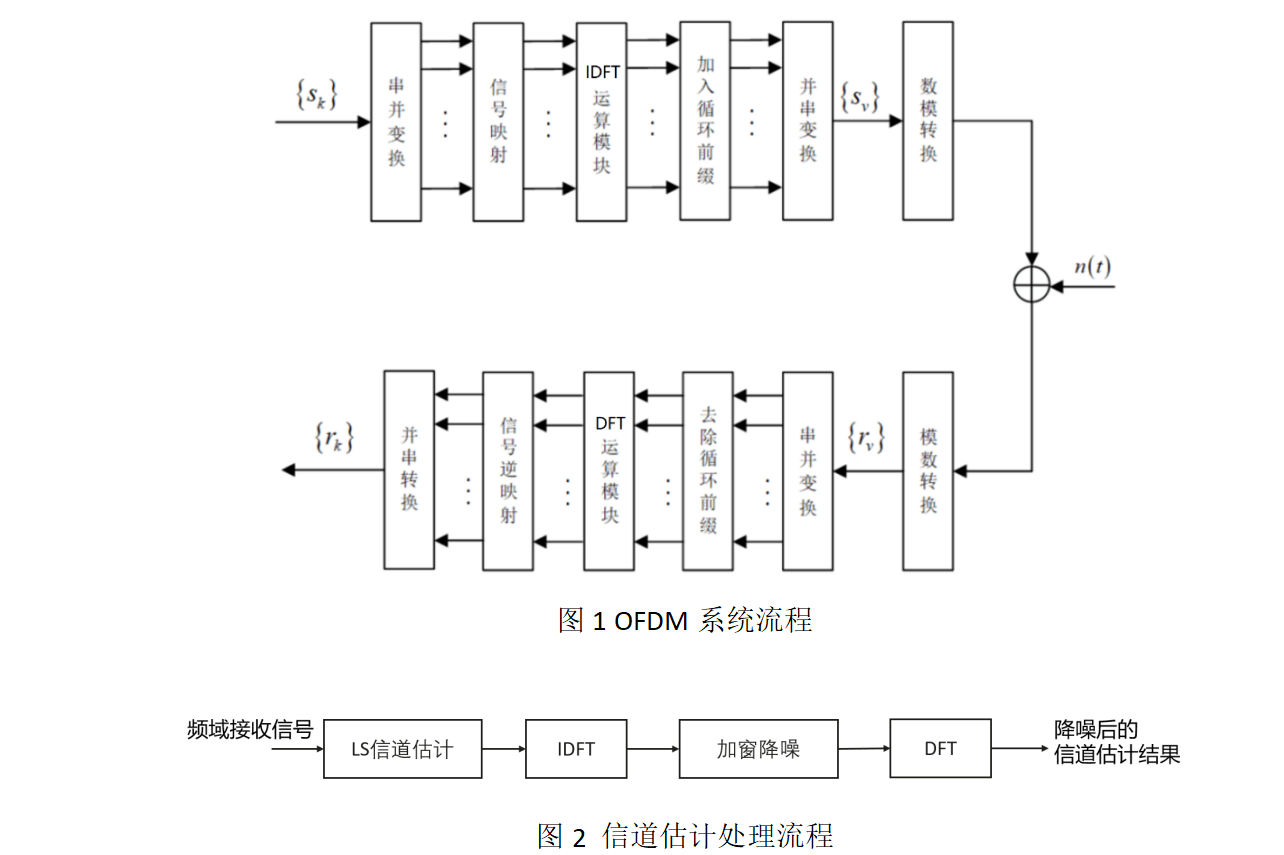
在芯片设计中,DFT计算的硬件复杂度与其算法复杂度和数据元素取值范围相关。算法复杂度越高、数据取值范围越大,其硬件复杂度就越大。目前在实际产品中,一般采用快速傅里叶变换(Fast Fourier Transform,FFT)算法来快速实现DFT,其利用DFT变换的各种性质,可以大幅降低DFT的计算复杂度(参见[1][2])。然而,随着无线通信技术的演进,天线阵面越来越大,通道数越来越多,通信带宽越来越大,对FFT的需求也越来越大,从而导致专用芯片上实现FFT的硬件开销也越大。为进一步降低芯片资源开销,一种可行的思路是将DFT矩阵分解成整数矩阵连乘的形式。
📚2 详细数学模型及题目、数据
链接:https://pan.baidu.com/s/1xBW-DjaT_Jt2jfrW_CUPLw
提取码:l662
--来自百度网盘超级会员V4的分享
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
- James W. Cooley and John W. Tukey, An Algorithm for the Machine Calculation of Complex Fourier Series, Mathematics of Computation, vol. 19, no. 90, pp. 297-301, 1965. DOI:10.2307/2003354.
- K. R. Rao, D. N. Kim, and J. J. Hwang, Fast Fourier Transform: Algorithms and Applications, Springer, 2010. (中译本:快速傅里叶变换:算法与应用,万帅,杨付正译,机械工业出版社,2012.)
- Viduneth Ariyarathna, Arjuna Madanayake, Xinyao Tang, Diego Coelho, et al, Analog Approximate-FFT 8/16-Beam Algorithms, Architectures and CMOS Circuits for 5G Beamforming MIMO Transceivers, IEEE Journal on Emerging and Selected Topics in Circuits and Systems, vol. 8, no. 3, pp. 466-479, 2018. DOI: 10.1109/JETCAS.2018.2832177.
🌈4 Matlab代码及思路实现
回复:华为杯B题

