Reference:

1. 深蓝学院-多传感器融合
2. 多传感器融合定位理论基础

文章跳转：

1. 多传感器融合定位一-3D激光里程计其一：ICP
2. 多传感器融合定位二-3D激光里程计其二：NDT
3. 多传感器融合定位三-3D激光里程计其三：点云畸变补偿
4. 多传感器融合定位四-3D激光里程计其四：点云线面特征提取
5. 多传感器融合定位五-点云地图构建及定位
6. 多传感器融合定位六-惯性导航原理及误差分析
7. 多传感器融合定位七-惯性导航解算及误差分析其一
8. 多传感器融合定位八-惯性导航解算及误差分析其二
9. 多传感器融合定位九-基于滤波的融合方法Ⅰ其一
10. 多传感器融合定位十-基于滤波的融合方法Ⅰ其二
11. 多传感器融合定位十一-基于滤波的融合方法Ⅱ
12. 多传感器融合定位十二-基于图优化的建图方法其一
13. 多传感器融合定位十三-基于图优化的建图方法其二
14. 多传感器融合定位十四-基于图优化的定位方法
15. 多传感器融合定位十五-多传感器时空标定(综述)

1. 编码器运动模型及标定

1.1 编码器基础知识

编码器感应轮子的旋转，并在旋转时输出脉冲，脉冲数与转过的角度呈线性比例关系。

脉冲对应的是角度增量，有时也用增量除以时间，转成轮子转动的角速度输出。

需要注意的是，编码器只是各种转角测量方式中的一种，其他还有轮速计、霍尔传感器等，本课程以编码器为例子讲解模型，但同样适用于其他形式的传感器。

编码器安装方式有单轮、双轮、三轮，本课程推导仅围绕双轮差分模型进行展开。
该模型中，需要用到以下变量：

• ${\mathbf{r}}_L$：左轮半径
• ${\mathbf{r}}_R$：右轮半径
• $\mathbf{d}$：轮子离底盘中心的距离
• ${\mathbf{\omega }}_L$：左轮自转角速度
• ${\mathbf{\omega }}_{\mathbf{R}}$：右轮自转角速度
• ${\mathbf{v}}_L$：左轮线速度
• ${\mathbf{v}}_R$：右轮线速度

实际使用时，标定完成后， ${\mathbf{r}}_L$、${\mathbf{r}}_R$、$\mathbf{d}$ 为固定参数， ${\mathbf{\omega }}_L$ 和 ${\mathbf{\omega }}_R$ 为测量值，而 ${\mathbf{v}}_L$ 和 ${\mathbf{v}}_R$ 可以通过下式计算得到：
$$\begin{array}{rl}{\mathbf{v}}_L& ={\mathbf{\omega }}_L{\mathbf{r}}_L\\ {\mathbf{v}}_R& ={\mathbf{\omega }}_R{\mathbf{r}}_R\end{array}$$

1.2 编码器运动模型

运动模型的作用是，使用前述已知量，求解以下变量：
$\mathbf{\omega }$ : 底盘中心的角速度
$\mathbf{v}$ : 底盘中心的线速度
$\mathbf{r}$ : 底盘中心圆弧运动旋转半径

1.2.1 旋转半径求解

双轮差分模型下，左右轮圆弧运动的角速度相等，且等于底盘中心圆弧运动的角速度(两个轮子的自转角速度是相同的)，因此有：
$$\mathbf{\omega }=\frac{{\mathbf{v}}_L}{\mathbf{r}-\mathbf{d}}=\frac{{\mathbf{v}}_R}{\mathbf{r}+\mathbf{d}}$$由此可以得出：
$${\mathbf{v}}_L(\mathbf{r}+\mathbf{d})={\mathbf{v}}_R(\mathbf{r}-\mathbf{d})$$移项可得：
$$\left({\mathbf{v}}_R-{\mathbf{v}}_L\right)\mathbf{r}=\left({\mathbf{v}}_R+{\mathbf{v}}_L\right)\mathbf{d}$$从而可以得到：
$$\mathbf{r}=\frac{{\mathbf{v}}_R+{\mathbf{v}}_L}{{\mathbf{v}}_R-{\mathbf{v}}_L}\mathbf{d}$$

1.2.2 角速度求解

把旋转半径的求解结果，代入角速度公式，即可得到：
$$\mathbf{\omega }=\frac{{\mathbf{v}}_L}{\frac{{\mathbf{v}}_R+{\mathbf{v}}_L}{{\mathbf{v}}_R-{\mathbf{v}}_L}\mathbf{d}-\mathbf{d}}=\frac{{\mathbf{v}}_R-{\mathbf{v}}_L}{2\mathbf{d}}$$

1.2.3 线速度求解

利用旋转角速度和旋转半径的结果，可以直接得到线速度：
$$\mathbf{v}=\mathbf{\omega }\mathbf{r}=\frac{{\mathbf{v}}_R-{\mathbf{v}}_L}{2\mathbf{d}}\frac{{\mathbf{v}}_R+{\mathbf{v}}_L}{{\mathbf{v}}_R-{\mathbf{v}}_L}\mathbf{d}=\frac{{\mathbf{v}}_R+{\mathbf{v}}_L}{2}$$

1.2.4 位姿求解

假设 ${\mathbf{x}}_k,{\mathbf{y}}_k,{\mathbf{\theta }}_k$ 为当前时刻位姿，${\mathbf{x}}_{k-1},{\mathbf{y}}_{k-1},{\mathbf{\theta }}_{k-1}$ 为上一时刻的位姿，则有：
$$\begin{array}{rl}& {\mathbf{\theta }}_k={\mathbf{\theta }}_{k-1}+\mathbf{\omega }\Delta t\\ & {\mathbf{x}}_k={\mathbf{x}}_{k-1}+\mathbf{v}\Delta t\cos \left({\mathbf{\theta }}_{\mathbf{k}-1}\right)\\ & {\mathbf{y}}_k={\mathbf{y}}_{k-1}+\mathbf{v}\Delta t\sin \left({\mathbf{\theta }}_{\mathbf{k}-1}\right)\end{array}$$其中：
$$\Delta t=t_k-t_{k-1}$$

1.3 编码器的标定

标定可以理解为运动模型求解过程的反向过程，具体是指在已知底盘中心线速度、角速度的情况下，求解轮子半径、轮子离底盘中心距离等。
已知量：
$v$：底盘中心的线速度
$\omega$：底盘中心的角速度
待求解量：
${\mathbf{r}}_L$：左轮半径
${\mathbf{r}}_R$：右轮半径
$\mathbf{d}$：轮子离底盘中心的距离
实际标定时，线速度、角速度由其他传感器提供(比如雷达点云和地图匹配)，且为了简化模型，认为雷达装在底盘中心正上方。(这里雷达最好的方法是先建好一个点云地图，然后在点云地图里面匹配，然后拿它做观测，去提供线速度和角速度的结果，而不要用激光里程计-----里程计本身就是有累计误差的)

1.3.1 轮子半径标定

由于速度的求解公式为：
$$\mathbf{v}=\frac{{\mathbf{v}}_R+{\mathbf{v}}_L}{2}=\frac{{\mathbf{\omega }}_R{\mathbf{r}}_R+{\mathbf{\omega }}_L{\mathbf{r}}_L}{2}$$它可以重新写为：
$$\left[\begin{array}{ll}{\mathbf{\omega }}_R& {\mathbf{\omega }}_L\end{array}\right]\left[\begin{array}{l}{\mathbf{r}}_R\\ {\mathbf{r}}_L\end{array}\right]=2\mathbf{v}$$当有多组测量值时，可以构成如下方程组：
$$\left[\begin{array}{cc}{\mathbf{\omega }}_{R0}& {\mathbf{\omega }}_{L0}\\ {\mathbf{\omega }}_{R1}& {\mathbf{\omega }}_{L1}\\ ⋮& ⋮\\ {\mathbf{\omega }}_{RN}& {\mathbf{\omega }}_{LN}\end{array}\right]\left[\begin{array}{l}{\mathbf{r}}_R\\ {\mathbf{r}}_L\end{array}\right]=\left[\begin{array}{c}2{\mathbf{v}}_0\\ 2{\mathbf{v}}_1\\ ⋮\\ 2{\mathbf{v}}_N\end{array}\right]$$这是典型的最小二乘问题，可用最小二乘标准形式计算。

1.3.2 轮子与底盘中心距离标定

由于角速度的求解公式为：
$$\mathbf{\omega }=\frac{{\mathbf{v}}_R-{\mathbf{v}}_{\mathbf{L}}}{2\mathbf{d}}$$在经过轮子半径标定之后，分子上的两项可认为是已知量，因此可以得到：
$$\mathbf{d}=\frac{{\mathbf{v}}_R-{\mathbf{v}}_L}{2\mathbf{\omega }}$$虽然可直接求解，但是为了抑制噪声带来的影响，因多次采样计算取平均。

2. 融合编码器的滤波方法

2.1 核心思路

在上一节课滤波模型的基础上增加编码器进行融合，有一种非常简单的方法，即使用编码器解算的速度作为观测量，加入原来模型的观测方程中，而其他环节保持不变。

2.2 观测量定义

编码器提供的是载体系下的速度观测，在前 $(\mathrm{x})$-左 $(\mathrm{y})$-上(z)坐标系的定义下，$\mathrm{x}$ 方向的速度分量是已知的 ${\mathbf{v}}_x^b={\mathbf{v}}_m$。 另外，在以车作为载体的情况下，由于车的侧向和天向没有运动，因此又有 ${\mathbf{v}}_y^b=0$，${\mathbf{v}}_z^b=0$。
基于此，我们可以认为 $b$ 系 3 个维度的速度分量都是可观测的。

2.3 观测方程推导

由于导航解算得到的是 $w$ 系下得速度，而速度观测是 $b$ 系下得，因此需要推导二者之间的误差关系，才能得到相应的观测方程。
推导方法仍按照第6讲的固定套路进行。

1. 写出不考虑误差时的方程：
   $${\mathbf{v}}^b={\mathbf{R}}_{bw}{\mathbf{v}}^w$$
2. 写出考虑误差时的方程：
   $${\tilde{\mathbf{v}}}^b={\tilde{\mathbf{R}}}_{bw}{\tilde{\mathbf{v}}}^w$$
3. 写出真实值与理想值之间的关系：
   $$\begin{array}{rl}& {\tilde{\mathbf{v}}}^b={\mathbf{v}}^b+\delta {\mathbf{v}}^b\\ & {\tilde{\mathbf{v}}}^w={\mathbf{v}}^w+\delta {\mathbf{v}}^w\\ & {\tilde{\mathbf{R}}}_{bw}={\tilde{\mathbf{R}}}_{wb}^T={\left({\mathbf{R}}_{wb}\left(\mathbf{I}+[\delta \mathbf{\theta }{]}_{\times }\right)\right)}^T\\ & =\left(\mathbf{I}-[\delta \mathbf{\theta }{]}_{\times }\right){\mathbf{R}}_{bw}\end{array}$$
4. 把3)中的关系带入2)式：
   $${\mathbf{v}}^b+\delta {\mathbf{v}}^b=\left(\mathbf{I}-[\delta \mathbf{\theta }{]}_{\times }\right){\mathbf{R}}_{bw}\left({\mathbf{v}}^w+\delta {\mathbf{v}}^w\right)$$
5. 把1)中的关系带入4)式：
   $${\mathbf{R}}_{bw}{\mathbf{v}}^w+\delta {\mathbf{v}}^b=\left(\mathbf{I}-[\delta \mathbf{\theta }{]}_{\times }\right){\mathbf{R}}_{bw}\left({\mathbf{v}}^w+\delta {\mathbf{v}}^w\right)$$
6. 化简方程：
   $$\begin{array}{rl}\delta {\mathbf{v}}^b& ={\mathbf{R}}_{bw}\delta {\mathbf{v}}^w-[\delta \mathbf{\theta }{]}_{\times }{\mathbf{R}}_{bw}{\mathbf{v}}^w\\ & ={\mathbf{R}}_{bw}\delta {\mathbf{v}}^w-[\delta \mathbf{\theta }{]}_{\times }{\mathbf{v}}^b\\ & ={\mathbf{R}}_{bw}\delta {\mathbf{v}}^w+{\left[{\mathbf{v}}^b\right]}_{\times }\delta \mathbf{\theta }\end{array}$$

根据前一章内容，状态量为
$$\delta \mathbf{x}=\left[\begin{array}{c}\delta \mathbf{p}\\ \delta \mathbf{v}\\ \delta \mathbf{\theta }\\ \delta {\mathbf{b}}_a\\ \delta {\mathbf{b}}_{\omega }\end{array}\right]$$而融合编码器以后，观测量变为
$$\mathbf{y}=\left[\begin{array}{c}\delta \overline{\mathbf{p}}\\ \delta {\overline{\mathbf{v}}}^b\\ \delta \overline{\mathbf{\theta }}\end{array}\right]$$其中 $\delta {\overline{\mathbf{v}}}^b$ 的观测值可以通过下式获得
$$\delta {\overline{\mathbf{v}}}_b={\tilde{\mathbf{v}}}^b-{\mathbf{v}}^b={\tilde{\mathbf{R}}}_{bw}{\tilde{\mathbf{v}}}^w-\left[\begin{array}{c}{\mathbf{v}}_m\\ 0\\ 0\end{array}\right]$$此时的观测方程 $\mathbf{y}={\mathbf{G}}_t\delta \mathbf{x}+{\mathbf{C}}_t\mathbf{n}$ 中的各变量应重新写为
$$\begin{array}{rl}& {\mathbf{G}}_t=\left[\begin{array}{ccccc}{\mathbf{I}}_3& 0& 0& 0& 0\\ 0& {\mathbf{R}}_{bw}& {\left[{\mathbf{v}}^b\right]}_{\times }& 0& 0\\ 0& 0& {\mathbf{I}}_3& 0& 0\end{array}\right]\\ & {\mathbf{C}}_t=\left[\begin{array}{ccc}{\mathbf{I}}_3& 0& 0\\ 0& {\mathbf{I}}_3& 0\\ 0& 0& {\mathbf{I}}_3\end{array}\right]\\ & \mathbf{n}={\left[\begin{array}{lllllllll}{n}_{\delta {\bar{p}}_x}& n_{\delta {\bar{p}}_y}& n_{\delta {\bar{p}}_z}& n_{\delta {\bar{v}}_x^b}& n_{\delta {\bar{v}}_y^b}& n_{\delta {\bar{v}}_z^b}& n_{\delta {\bar{\theta }}_x}& n_{\delta {\bar{\theta }}_y}& n_{\delta {\bar{\theta }}_z}\end{array}\right]}^T\end{array}$$随后，便可以使用新的观测方程，不改变其他方程，直接按照原有流程进行Kalman滤波融合。

3. 融合运动约束的滤波方法

很多时候，硬件平台并没有编码器，不能直接使用上一小节的模型，但是车本身的运动特性(即侧向速度和天向速度为0)仍然可以使用。

它对观测量带来的改变仅仅是少了一个维度($x$ 方向)，而推导方法并没有改变，因此此处直接给出该融合模式下的推导结果。

新的观测量为
$$\mathbf{y}=\left[\begin{array}{c}\delta \overline{\mathbf{p}}\\ {\left[\delta {\overline{\mathbf{v}}}^b\right]}_{yz}\\ \delta \overline{\mathbf{\theta }}\end{array}\right]$$$[\bullet {]}_{yz}$ 表示只取三维向量或矩阵的后2行

此时的观测方程 $\mathbf{y}={\mathbf{G}}_t\delta \mathbf{x}+{\mathbf{C}}_t\mathbf{n}$ 中的各变量应重新写为
$$\begin{array}{rl}& {\mathbf{G}}_t=\left[\begin{array}{ccccc}{\mathbf{I}}_3& 0& 0& 0& 0\\ 0& {\left[{\mathbf{R}}_{bw}\right]}_{yz}& {\left[{\left[{\mathbf{v}}^b\right]}_{\times }\right]}_{yz}& 0& 0\\ 0& 0& {\mathbf{I}}_3& 0& 0\end{array}\right]\\ & {\mathbf{C}}_t=\left[\begin{array}{ccc}{\mathbf{I}}_3& 0& 0\\ 0& {\mathbf{I}}_2& 0\\ 0& 0& {\mathbf{I}}_3\end{array}\right]\\ & \mathbf{n}={\left[\begin{array}{llllllll}{n}_{\delta {\bar{p}}_x}& n_{\delta {\bar{p}}_y}& n_{\delta {\bar{p}}_z}& n_{\delta {\bar{v}}_y^b}& n_{\delta {\bar{v}}_z^b}& n_{\delta {\bar{\theta }}_x}& n_{\delta {\bar{\theta }}_y}& n_{\delta {\bar{\theta }}_z}\end{array}\right]}^T\end{array}$$随后的Kalman流程仍然与之前保持一致。

4. 融合点云特征的滤波方法

4.1 整体思路

以IMU做状态预测，以特征中的点-面距离、点-线距离为约束(观测)，修正误差。

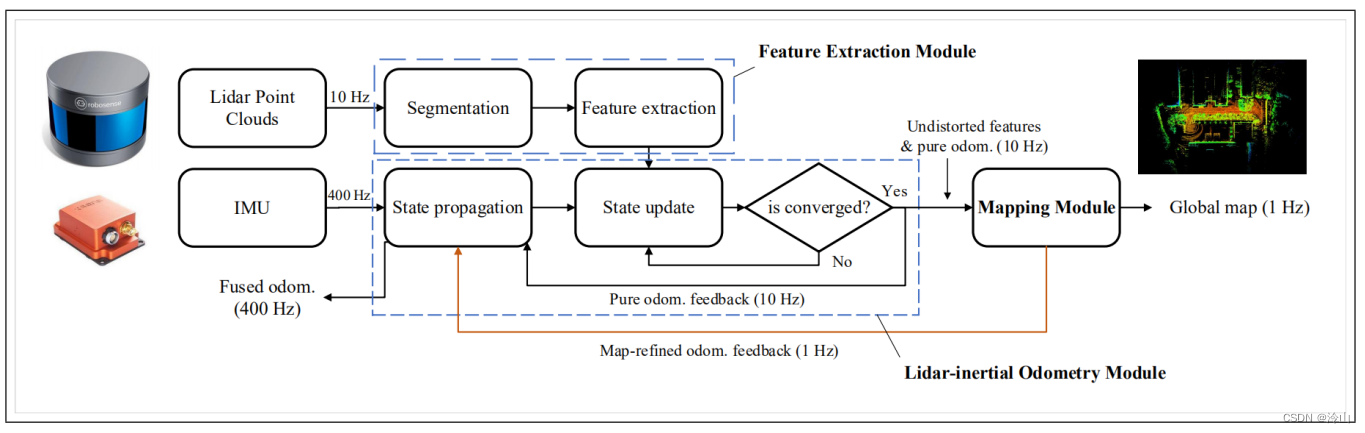
论文题目：LINS: A Lidar-Inertial State Estimator for Robust and Efficient Navigation

4.2 滤波模型

1. 状态定义
   位姿定义：
   $${\mathbf{x}}_w^{b_k}:=\left[{\mathbf{p}}_w^{b_k},{\mathbf{q}}_w^{b_k}\right]$$相对位姿相关：
   $${\mathbf{x}}_{b_{k+1}}^{b_k}:=\left[{\mathbf{p}}_{b_{k+1}}^{b_k},{\mathbf{v}}_{b_{k+1}}^{b_k},{\mathbf{q}}_{b_{k+1}}^{b_k},{\mathbf{b}}_a,{\mathbf{b}}_g,{\mathbf{g}}^{b_k}\right]$$状态量：
   $$\delta \mathbf{x}:=\left[\delta \mathbf{p},\delta \mathbf{v},\delta \mathbf{\theta },\delta {\mathbf{b}}_a,\delta {\mathbf{b}}_g,\delta \mathbf{g}\right]$$状态量修正：
   $${\mathbf{x}}_{b_{k+1}}^{b_k}={}^{-}{\mathbf{x}}_{b_{k+1}}^{b_k}⊞\mathbf{\delta }\mathbf{x}=\left[\begin{array}{c}-{\mathbf{p}}_{b_{k+1}}^{b_k}+\mathbf{\delta }\mathbf{p}\\ -{\mathbf{v}}_k^{b_k}+\mathbf{\delta }\mathbf{v}\\ -{\mathbf{q}}_{b_{k+1}}^{b_k}\otimes \exp (\mathbf{\delta }\mathbf{\theta })\\ -{\mathbf{b}}_a+\mathbf{\delta }{\mathbf{b}}_a\\ -{\mathbf{b}}_g+\delta {\mathbf{b}}_g\\ -{\mathbf{g}}^{b_k}+\mathbf{\delta }\mathbf{g}\end{array}\right]$$其中 ${}^{-}{\mathbf{x}}_{b_{k+1}}^{b_k}$ 表示预测值。

2. 状态方程
   $$\delta \dot{\mathbf{x}}(t)={\mathbf{F}}_t\delta \mathbf{x}(t)+{\mathbf{G}}_t\mathbf{w}$$其中
   $$\begin{array}{rl}{\mathbf{F}}_t& =\left[\begin{array}{cccccc}0& \mathbf{I}& 0& 0& 0& 0\\ 0& 0& -{\mathbf{R}}_t^{b_k}{\left[{\hat{\mathbf{a}}}_t\right]}_{\times }& -{\mathbf{R}}_t^{b_k}& 0& -{\mathbf{I}}_3\\ 0& 0& -{\left[{\hat{\omega }}_t\right]}_{\times }& 0& -{\mathbf{I}}_3& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]{\mathbf{G}}_t=\left[\begin{array}{cccc}0& 0& 0& 0\\ -{\mathbf{R}}_t^{b_k}& 0& 0& 0\\ 0& -{\mathbf{I}}_3& 0& 0\\ 0& 0& {\mathbf{I}}_3& 0\\ 0& 0& 0& {\mathbf{I}}_3\\ 0& 0& 0& 0\end{array}\right]\\ \mathbf{w}& ={\left[{\mathbf{n}}_a^T,{\mathbf{n}}_g^T,{\mathbf{n}}_{b_a}^T,{\mathbf{n}}_{b_g}^T\right]}^T\end{array}$$

3. 观测方程
   观测的计算与loam中前后帧匹配的思想一致，都是计算 点-面、点-线的残差
   其中
   $${\hat{\mathbf{p}}}_i^{l_k}={\left({\mathbf{R}}_l^b\right)}^T\left({\mathbf{R}}_{b_{k+1}}^{b_k}\left({\mathbf{R}}_l^b{\mathbf{p}}_i^{l_{k+1}}+{\mathbf{p}}_l^b\right)+{\mathbf{p}}_{b_{k+1}}^{b_k}-{\mathbf{p}}_l^b\right)$$为了计算观测方程，需要计算残差对状态量的雅可比
   $${\mathbf{H}}_k=\frac{\partial \mathbf{f}}{\partial {\hat{\mathbf{p}}}_i^{l_k}}\cdot \frac{\partial {\hat{\mathbf{p}}}_i^{l_k}}{\partial \delta \mathbf{x}}$$上式中包含两部分，第一部分已经讲过，此处只推导第 二部分。
   除了旋转和平移外，残差项对其它量的导数均为 0 。
   a.对平移求导
   $$\begin{array}{rl}& \frac{\partial {\hat{\mathbf{p}}}_i^{l_k}}{\partial \delta \mathbf{p}}\\ =& \frac{\partial \left[{\left({\mathbf{R}}_l^b\right)}^{\top }\left({\mathbf{R}}_{b_{k+1}}^{b_k}\left({\mathbf{R}}_l^b{\mathbf{p}}_i^{l_{k+1}}+{\mathbf{p}}_l^b\right)+{\mathbf{p}}_{b_{k+1}}^{b_k}-{\mathbf{p}}_l^b\right)\right]}{\partial \delta \mathbf{p}}\\ =& \frac{\partial \left[{\left({\mathbf{R}}_l^b\right)}^{\top }{\mathbf{p}}_{b_{k+1}}^{b_k}\right]}{\partial \delta \mathbf{p}}\\ =& {\left({\mathbf{R}}_l^b\right)}^{\top }\end{array}$$b.对旋转求导
   $$\begin{array}{rl}& \frac{\partial {\hat{\mathbf{p}}}_i^{l_k}}{\partial \delta \mathbf{x}}\\ =& \frac{\partial \left[{\left({\mathbf{R}}_l^b\right)}^T\left({\mathbf{R}}_{b_{k+1}}^{b_k}\left({\mathbf{R}}_l^b{\mathbf{p}}_i^{l_{k+1}}+{\mathbf{p}}_l^b\right)+{\mathbf{p}}_{b_{k+1}}^{b_k}-{\mathbf{p}}_l^b\right)\right]}{\partial \delta \mathbf{\theta }}\\ =& {\left({\mathbf{R}}_l^b\right)}^T\frac{\partial \left[{\mathbf{R}}_{b_{k+1}}^{b_k}\left({\mathbf{R}}_l^b{\mathbf{p}}_i^{l_{k+1}}+{\mathbf{p}}_l^b\right)\right]}{\partial {\mathbf{R}}_{b_{k+1}}^{b_k}}\frac{\partial {\mathbf{R}}_{b_{k+1}}^{b_k}}{\partial \delta \mathbf{\theta }}\\ =& -{\left({\mathbf{R}}_l^b\right)}^T{\left[{\mathbf{R}}_{b_{k+1}}^{b_k}\left({\mathbf{R}}_l^b{\mathbf{p}}_i^{l_{k+1}}+{\mathbf{p}}_l^b\right)\right]}_{\times }{\mathbf{R}}_{b_{k+1}}^{b_k}{\mathbf{J}}_r^{-1}(\mathbf{\theta })\\ =& -{\left({\mathbf{R}}_l^b\right)}^T{\mathbf{R}}_{b_{k+1}}^{b_k}{\left[{\mathbf{R}}_l^b{\mathbf{p}}_i^{l_{k+1}}+{\mathbf{p}}_l^b\right]}_{\times }{\mathbf{R}}_{b_k}^{b_{k+1}}{\mathbf{R}}_{b_{k+1}}^{b_k}{\mathbf{J}}_r^{-1}(\mathbf{\theta })\\ =& -{\left({\mathbf{R}}_l^b\right)}^T{\mathbf{R}}_{b_{k+1}}^{b_k}{\left[{\mathbf{R}}_l^b{\mathbf{p}}_i^{l_{k+1}}+{\mathbf{p}}_l^b\right]}_{\times }{\mathbf{J}}_r^{-1}(\mathbf{\theta })\end{array}$$预测 :
   $$\begin{array}{rl}& \delta {\mathbf{x}}_{t_{\tau }}=\left(\mathbf{I}+{\mathbf{F}}_{t_{\tau }}\Delta t\right)\delta {\mathbf{x}}_{t_{\tau -1}}\\ & {\mathbf{P}}_{t_{\tau }}=\left(\mathbf{I}+{\mathbf{F}}_{t_{\tau }}\Delta t\right){\mathbf{P}}_{t_{\tau -1}}{\left(\mathbf{I}+{\mathbf{F}}_{t_{\tau }}\Delta t\right)}^T+\left({\mathbf{G}}_{i_{\tau }}\Delta t\right)\mathbf{Q}{\left({\mathbf{G}}_{t_t}\Delta t\right)}^T\\ & {\mathbf{K}}_{k,j}={\mathbf{P}}_k{\mathbf{H}}_{k,j}^T{\left({\mathbf{H}}_{k,j}{\mathbf{P}}_k{\mathbf{H}}_{k,j}^T+{\mathbf{J}}_{k,j}{\mathbf{M}}_k{\mathbf{J}}_{k,j}^T\right)}^{-1}\end{array}$$迭代观测: $\Delta {\mathbf{x}}_j={\mathbf{K}}_{k,j}\left({\mathbf{H}}_{k,j}\delta {\mathbf{x}}_j-f\left({}^{-}{\mathbf{x}}_{b_{k+1}}^{b_k}⊞\mathbf{\delta }{\mathbf{x}}_j\right)\right)$
   $$\delta {\mathbf{x}}_{j+1}=\delta {\mathbf{x}}_j+\Delta {\mathbf{x}}_j$$后验方差: ${\mathbf{P}}_{k+1}=\left(\mathbf{I}-{\mathbf{K}}_{k,n}{\mathbf{H}}_{k,n}\right){\mathbf{P}}_k{\left(\mathbf{I}-{\mathbf{K}}_{k,n}{\mathbf{H}}_{k,n}\right)}^T+{\mathbf{K}}_{k,n}{\mathbf{M}}_k{\mathbf{K}}_{k,n}^T$

4.3 位姿更新

$${\mathbf{x}}_w^{b_{k+1}}=\left[\begin{array}{c}{\mathbf{p}}_w^{b_{k+1}}\\ {\mathbf{q}}_w^{b_{k+1}}\end{array}\right]=\left[\begin{array}{c}{\mathbf{R}}_{b_k}^{b_{k+1}}\left({\mathbf{p}}_w^{b_k}-{\mathbf{p}}_{b_{k+1}}^{b_k}\right)\\ {\mathbf{q}}_{b_k}^{b_{k+1}}\otimes {\mathbf{q}}_w^{b_k}\end{array}\right]$$

4.4 相似工作

论文题目：FAST-LIO: A Fast, Robust LiDAR-inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter