当前位置：首页 > news >正文

【数据结构】二叉树的·深度优先遍历（前中后序遍历）and·广度优先（层序遍历）

news 2025/7/7 23:05:50

在这里插入图片描述

💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃个人主页：阿然成长日记 👈点击可跳转
📆 个人专栏： 🔹数据结构与算法🔹C语言进阶
🚩 不能则学，不知则问，耻于问人，决无长进
🍭 🍯 🍎 🍏 🍊 🍋 🍒 🍇 🍉 🍓 🍑 🍈 🍌 🍐 🍍

文章目录

一、二叉树的深度优先遍历
- 🌺1.前序遍历
- - （1）`先序遍历`的过程：
  - （2）流程图：
  - （3）代码：
  - （4）测试结果：
- 🌼2.中序遍历
- - （1）`中序遍历`的过程：
  - （2）代码：
  - （3）测试结果：
- 🌻3.后序遍历
- - （1) `后序遍历`的过程：
  - （2）代码：
  - （3）测试结果：
二、【广度优先】层序遍历
- 1.思路及过程：
- 2.代码
- 3.测试结果

一、二叉树的深度优先遍历

🌺1.前序遍历

（1）`先序遍历`的过程：

1.先访问当前节点（即根节点）

2.遍历当前节点的左节点，再同样遍历左子树中的节点

3.遍历完当前节点的左子树后，再去遍历当前节点的右子树，再遍历右子树中的节点

总结：先访问根节点，然后遍历左子树，最后遍历右子树；即根左右

（2）流程图：

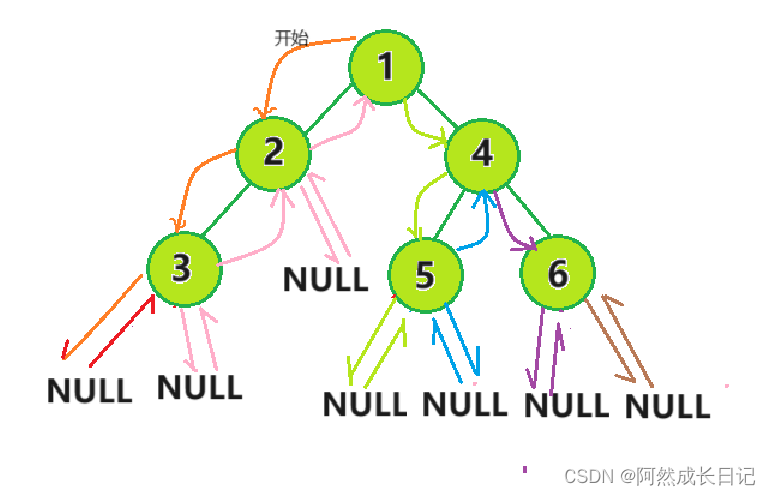
在这里插入图片描述

（3）代码：

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}

（4）测试结果：

1->2->3->NULL->NULL->NULL->4->5->NULL->NULL->6->NULL->NULL

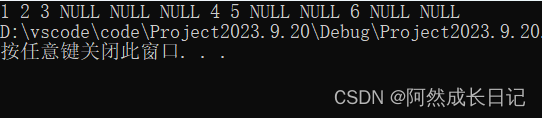
在这里插入图片描述

🌼2.中序遍历

（1）`中序遍历`的过程：

1.先进入当前节点的左子树，以同样的步骤遍历左子树的节点

2.访问当前节点

3.最后进入到当前节点的右子树，以同样的步骤遍历右子树中的节点

总结：先遍历左子树，再访问根节点，最后遍历右子树，即左根右

（2）代码：


// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreePrevOrder(root->_left);printf("%d ", root->_data);BinaryTreePrevOrder(root->_right);
}

（3）测试结果：

NULL->3->NULL->2->NULL->1->NULL->5->4->NULL->6->NULL

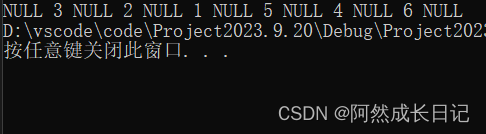
在这里插入图片描述

🌻3.后序遍历

（1) `后序遍历`的过程：

1.先进入当前节点的左子树，以同样的步骤遍历左子树中的节点

2.再进入当前节点的右子树，以同样的步骤去遍历右子树中的节点

3.最后遍历此左子树和右子树的父亲节点，也就是该节点

总结：先遍历左子树，再遍历右子树，最后访问根节点，即左右根

（2）代码：

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);printf("%d ", root->_data);
}

（3）测试结果：

NULL->NULL->3->NULL->2->NULL->NULL->5->NULL->NULL->6->4->1
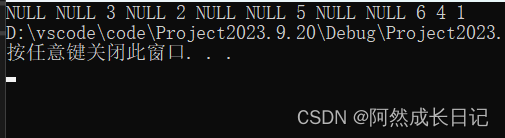
在这里插入图片描述

二、【广度优先】层序遍历

1.思路及过程：

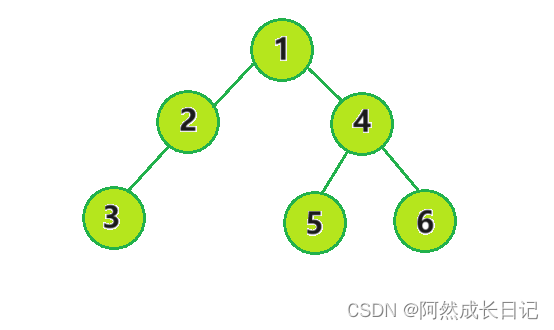
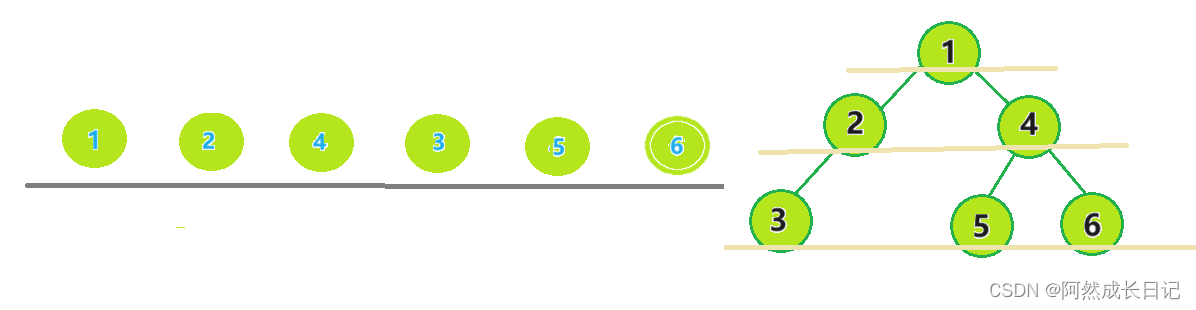
构建一颗二叉树
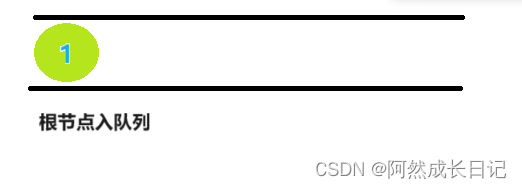
在这里插入图片描述
1.将root节点1放入队列。

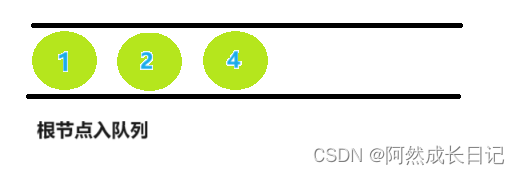
2.取队列首元素1，并将节点1的左右孩子入队

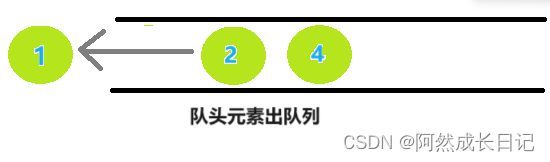
3.队首元素出队列

4.取队列首元素2，并将节点2的左右孩子入队，由于只有左孩子，所以只用入队一个元素。

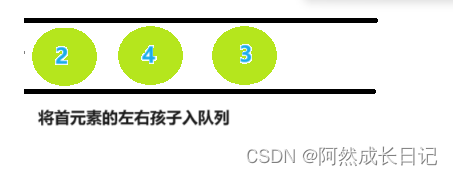
5.队首元素出队列
在这里插入图片描述
6.取队列首元素4，并将节点4的左右孩子入队。

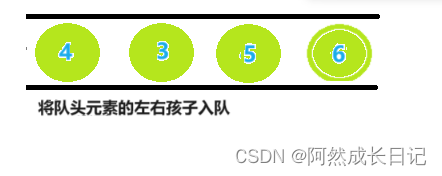
7.队首元素出队列

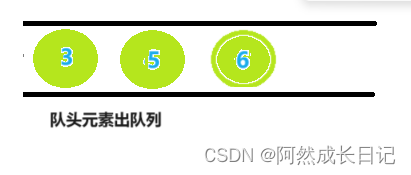
8.取队列首元素3，并将节点3的左右孩子入队。但是，元素3左右孩子为NULL，因此不用入队。直接执行出队列操作。

9.取队列首元素5，并将节点5的左右孩子入队。但是，元素5左右孩子为NULL，因此不用入队。直接执行出队列操作.
在这里插入图片描述

10.取队列首元素6，并将节点6的左右孩子入队。但是，元素6左右孩子为NULL，因此不用入队。直接执行出队列操作。
在这里插入图片描述
11.到此，队列元素已全部出队，层序遍历完成！
结果为：

2.代码

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Que q;QueueInit(&q);if (root)QueuePush(&q,root);while (!QueueEmpty(&q)){BTNode* tmp = QueueFront(&q);printf("%d ", tmp->_data);if (tmp->_left){QueuePush(&q,tmp->_left);}if (tmp->_right){QueuePush(&q, tmp->_right);}QueuePop(&q);}printf("\n");QueueDestroy(&q);
}