007 数据结构_堆——“C”
前言
本文将会向您介绍关于堆Heap的实现
具体步骤
tips:本文具体步骤的顺序并不是源代码的顺序
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;
初始化
void HeapCreate(Heap* hp, HPDataType* a, int n)
{hp->_a = NULL;hp->_size = 0;hp->_capacity = 0;
}
扩容
解析:扩容的逻辑很简单,没什么可讲的,要注意的点有这里不要使用malloc,当再次需要扩容的时候,malloc函数只会分配新的内存空间,不会复制原有内存空间的内容,realloc函数会在分配新的内存空间时,将原有内存内容复制到新的内存空间中,并释放原有空间内容//扩容
void CheckCapacity(Heap* hp)
{
if (hp->_capacity == hp->_size)
{int newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("malloc fail");return;}hp->_a = tmp;hp->_capacity = newcapacity;
}
}
判空
// 堆的判空
bool HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0;
}
交换
解析:这里提供了一个swap函数用于向上调整和向下调整时交换数据
//交换
void swap(int* a, int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
插入
每次插入的数据都会进行向上调整,将一串数据建成小堆/大堆
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{CheckCapacity(hp);hp->_a[hp->_size] = x;hp->_size++;Adjustup(hp->_a, hp->_size - 1);
}
向上调整
当插入数据时,注意每次插入一个数据都会向上调整(直到根结点)图中这里只是将结构画了出来助于理解,真实的情况中并不是向右边的堆图一样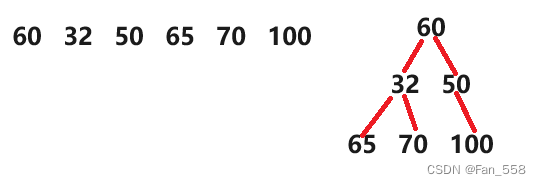
以小堆为例,当a[child] <a[parent]就将二者交换,并将parent 赋值给child,并利用新的child计算出新的parent,这样的做法是可以向上进行调整。这里若是将a[child] <a[parent]变成a[child] >a[parent]就是大堆
//向上调整
void Adjustup(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){swap(a, &a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
删除
解析:需要删除堆顶的数据,但是如果挪动数据删除堆顶的数据,可能会导致可能会导致堆的性质不满足,影响堆的正确性和效率。因此需要交换堆顶与末尾的数据,再将末尾的数据删除,这样一来就可以删除掉堆顶的数据,但是有个问题:将堆尾的数据调整到了堆顶,需要进行向下调整// 堆的删除 删除堆顶
void HeapPop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));swap(hp->_a, &(hp->_a[0]), &(hp->_a[hp->_size - 1]));--hp->_size;//向下调整AdjustDown(hp->_a, hp->_size, 0);
}
向下调整
解析:当我们删除堆顶数据的时候进行向下调整,n:堆的数据个数,利用parent计算出child下标
//向下调整
void AdjustDown(int* a, int n, int parent)
{//计算左child,相当于(child = leftchild)int child = parent * 2 + 1;//当逐步地向下调整,child会越来越大,child不能超过堆数据个数while (child < n){//向下调整的时候右child可能越界//找左右child小的那一个进行与a[parent]比较if (child + 1 < n && a[child + 1] < a[child]){//若是默认的child(leftchild) > a[child + 1]++child;}//可调整<(小堆)为>(大堆)if (a[child] < a[parent]){swap(a, &a[child], &a[parent]);//向下调整parent = child;child = parent * 2 + 1;}else{break;}}
}
销毁
// 堆的销毁
void HeapDestory(Heap* hp)
{free(hp->_a);hp->_a = NULL;hp->_capacity = 0;hp->_size = 0;
}
获取堆顶数据
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));return hp->_a[0];
}
获取个数
// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}
小结
本文的分享就到这里啦,如果本文存在疏漏或错误的地方还请您能够指出!
