积分值和面积、对称性
- 积分的基本含义要从积分符号说起,积分号含有加号的意思, ∫ a b f ( x ) d x \int ^b_af(x)dx ∫abf(x)dx可以理解为:区间[a,b]无限细分为无穷多个dx,无穷多个f(x)乘以dx的累积和。
- 根据上面的描述,面积可以理解为 ∫ a b ∣ f ( x ) ∣ d x , 并且 d x 为正向(即 a < b ) \int ^b_a |f(x)|dx,并且dx为正向(即a<b) ∫ab∣f(x)∣dx,并且dx为正向(即a<b)。f(x)取绝对值和dx的正向是为了保证积分表达式是正值,面积没有方向仅仅是一个标量。那么考虑一个问题:“积分值等于被积函数和积分元素x(or y)之间的面积”,这句话到底对不对呢?当然不全对。也就是说,这句话某些情况下是对的,某些情况下是错的。当被积函数的值在积分区间同号时是对的,当被积函数的值不同号时是错的,因为积分表达式f(x)dx有符号!
- 积分对称性的隐含条件也包含dx的正向。假设 f(x) 是偶函数,根据定义有f(-x) = f(x), dx大于0,则 ∫ − a a f ( x ) d x = 2 ∫ 0 a f ( x ) d x = 2 ∫ − a 0 f ( x ) d x ( 积分表达式 f ( x ) d x 处处相等 ) ( a > 0 ) \int ^{a}_{-a} f(x) dx = 2\int ^{a}_{0} f(x) dx =2 \int ^{0}_{-a} f(x) dx\color{red}(积分表达式f(x)dx处处相等)\color{black}(a>0) ∫−aaf(x)dx=2∫0af(x)dx=2∫−a0f(x)dx(积分表达式f(x)dx处处相等)(a>0);若f(x)是奇函数,根据奇函数的定义有f(-x) = - f(x),则 ∫ 0 a f ( x ) d x = − ∫ 0 a f ( − x ) d x = ∫ 0 − a f ( t ) d t ( 将 − x 带换为 t ) = − ∫ − a 0 f ( t ) d t ( a > 0 ) \int ^{a}_{0} f(x) dx =-\int ^{a}_{0} f(-x) dx = \int ^{-a}_{0} f(t) dt \color{red}(将-x带换为t)\color{black}= -\int ^{0}_{-a} f(t) dt(a>0) ∫0af(x)dx=−∫0af(−x)dx=∫0−af(t)dt(将−x带换为t)=−∫−a0f(t)dt(a>0),即可得到结论 ∫ − a a f ( x ) d x = 0 \int ^{a}_{-a} f(x) dx = 0 ∫−aaf(x)dx=0
参照下图帮助理解:
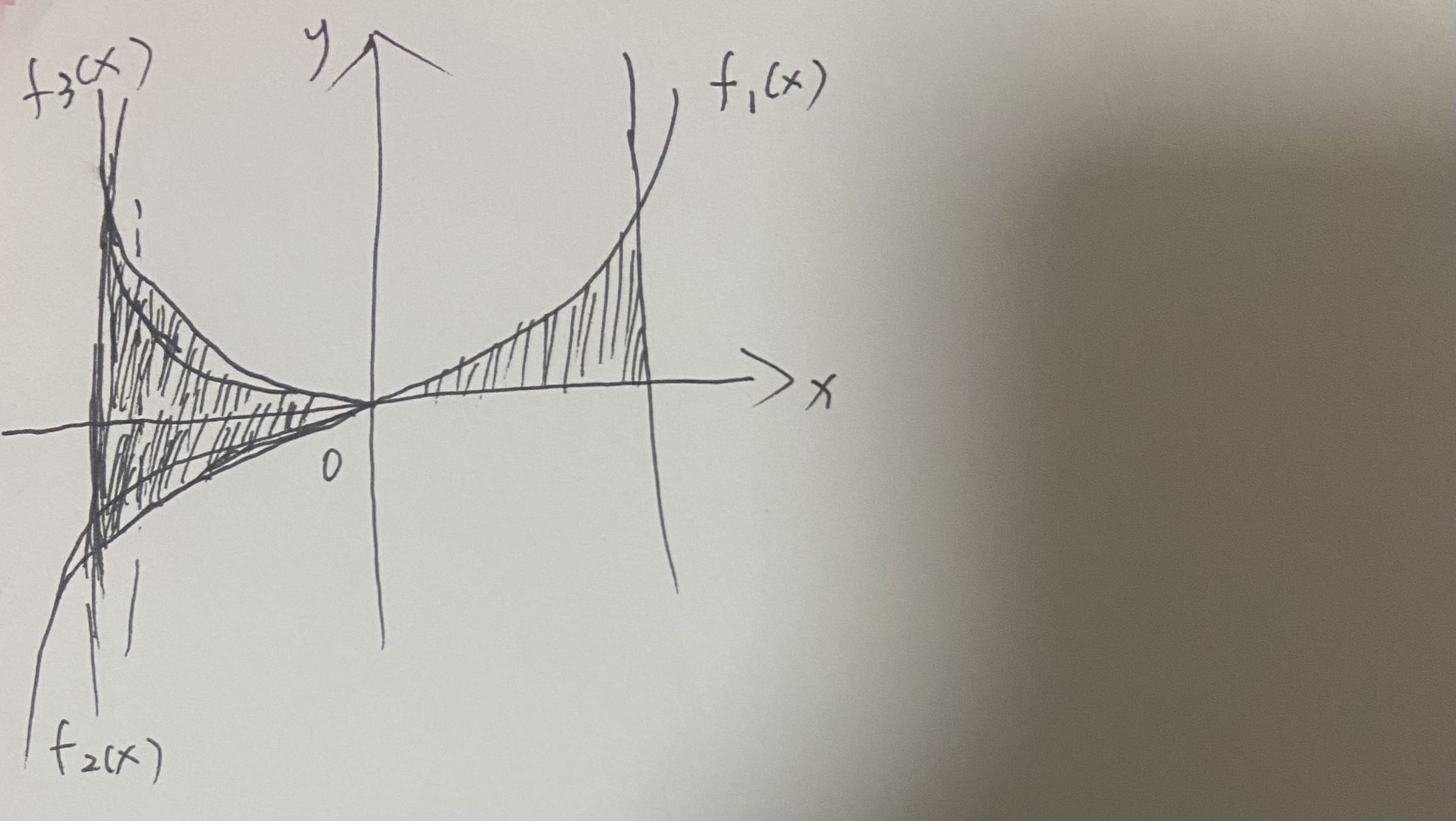
明白了这几者的关系,在碰到积分与面积、对称性有关的问题时,就不会犯迷糊了。
罗祥曾经说过一句话,“学习过于深入细节,这样的人,往往会失败,连通过考试都困难”。我觉得也是这样,学习没必要花费太多精力,牺牲自己绝大多数的精力和资源。创新讲究的是发散思维,学霸都是能集中注意力、用最少的时间获得最大收益的人。读书或者做事情过于苛刻会导致思想僵化、古板、钻牛角尖,这样的人往往只会死读书,读死书。
