当前位置：首页 > news >正文

【陕西理工大学-数学软件实训】数学实验报告（8）（数值微积分与方程数值求解）

news 2025/7/27 19:30:50

一、实验目的

二、实验要求

三、实验内容与结果

四、实验心得

一、实验目的

1. 掌握求数值导数和数值积分的方法。
2. 掌握代数方程数值求解的方法。
3. 掌握常微分方程数值求解的方法。

二、实验要求

1. 根据实验内容，编写相应的MATLAB程序，并将程序及结果放置于相应位置。
2. 实验内容与结果采用小四号宋体、1.5倍行距进行排版，其中图片的宽度不超过8cm。

三、实验内容与结果

1. 求函数在指定点的数值导数：

解：

MATLAB代码：
   syms x

% 创建一个3x3矩阵，其中x是参数
A = [x, x^2, x^3;
1, 2*x, 3*x^2;
0, 2, 6*x];

% 计算行列式
det_A = det(A);

% 展开行列式为函数
function_det = simplify(det_A);

% 求导数
df = diff(function_det,x);

% 输出导数
disp(df)
输出结果为：6*x^2
因此在x = 1时导数为6，x = 2，导数为24，x = 3，导数为54.

2. 用数值方法求定积分。

解： MATLAB代码： f = inline('sqrt(cos(t.^2)+4*sin(2*t).^2+1)'); I1 = quad(f,0,2*pi) g = inline('log(1+x)./(1+x.^2)'); I2 = quad(g,0,1) 输出结果：

3. 求代数方程的数值解。

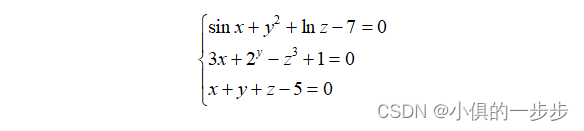
（1）：

function g=f(x)

g=3*c+sin(x)-exp(x);

求解： clc;clear; fzero(f,1.5)

结果：

（2）

function F=fun(X)
x=X(1);
y=X(2);
z=X(3);
F(1)=sin(x)+y^2+log(z)-7;
F(2)=3*x+2-z^3+1;
F(3)=x+y+z-5;
end

求解：

X=fsolve('fun',[1,1,1],optimset('Display',off))
输出结果：

4. 求函数在指定区间的极值。

解：function f=g(u)
a=u(1);
y=u(2);
x=a; % assuming x is meant to be the same as a
f=2*x.^3+4*x.*y.^3-10*x.*y+y.^2;
end

clc;
clear;
format long;
f=inline('(x^3+cos(x)+x*log(x))/exp(x)');
[x,fmin1]=fminbnd('f',0,1)
[U,fmin2]=fminsearch('g',[0,0])

输出结果：