数学小课堂:数学的线索(从猜想到定理再到应用的整个过程)
文章目录
- 引言
- I 勾股定理
- 1.1 勾三股四弦五
- 1.2 数学和自然科学的三个本质差别
- 1.3 总结
引言

从猜想到定理再到应用的整个过程是数学发展和体系构建常常经历的步骤。
I 勾股定理
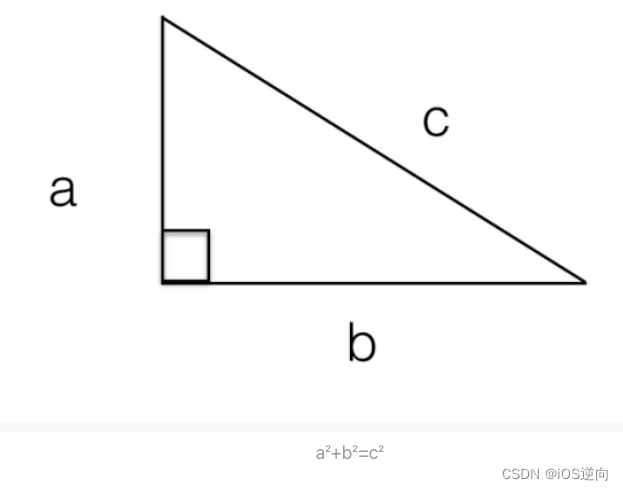
勾股定理: 直角三角形两条直角边的平方之和等于斜边的平方,这个定理在国外都被称为毕达哥拉斯定理。
毕达哥拉斯(Pythagoras,约公元前580年—约公元前500年)是古希腊著名的数学家和知识的集大成者。
1.1 勾三股四弦五
勾三股四弦五只不过是一个特例而已,光举例子还是不够的,还需要做出一个明确的规律性的描述,这种描述我们可以把它称为命题。一个命题在没有证明之前,只能算是猜想。
1.2 数学和自然科学的三个本质差别
- 测量和逻辑推理的区别:数学上的结论只能从定义和公理出发&#x