聚类(性能度量)
文章目录
- 聚类(性能度量)
- 外部指标
- 例1
- 内部指标
- 例2
聚类(性能度量)
对数据集 D={x1,x2,...,xm}D=\{x_1,x_2,...,x_m\}D={x1,x2,...,xm} ,假定通过聚类给出的簇划分为 C={C1,C2,...,Ck}C=\{C_1,C_2,...,C_k\}C={C1,C2,...,Ck} ,参考模型给出的簇划分为 C∗={C1∗,C2∗,...,Cs∗}C^*=\{C_1^*,C_2^*,...,C_s^*\}C∗={C1∗,C2∗,...,Cs∗} ,相应的,令 λ\lambdaλ 与 λ∗\lambda^*λ∗ 分别表示与 CCC 和 C∗C^*C∗ 对应的簇标记向量。我们将样本两两配对考虑,定义:
a=∣SS∣,SS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j}b=∣SD∣,SS={(xi,xj)∣λi=λj,λi∗≠λj∗,i<j}c=∣DS∣,SS={(xi,xj)∣λi≠λj,λi∗=λj∗,i<j}d=∣DD∣,SS={(xi,xj)∣λi≠λj,λi∗≠λj∗,i<j}a=\vert SS \vert,\quad SS=\{(x_i,x_j) \quad| \quad \lambda_i=\lambda_j,\lambda_i^*=\lambda_j^*,i<j\} \\ b=\vert SD \vert,\quad SS=\{(x_i,x_j) \quad| \quad \lambda_i=\lambda_j,\lambda_i^* \neq \lambda_j^*,i<j\} \\ c=\vert DS \vert,\quad SS=\{(x_i,x_j) \quad| \quad \lambda_i \neq \lambda_j,\lambda_i^*=\lambda_j^*,i<j\} \\ d=\vert DD \vert,\quad SS=\{(x_i,x_j) \quad| \quad \lambda_i \neq \lambda_j,\lambda_i^* \neq \lambda_j^*,i<j\} a=∣SS∣,SS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j}b=∣SD∣,SS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j}c=∣DS∣,SS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j}d=∣DD∣,SS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j}
其中,集合 SSSSSS 包含了在 CCC 中隶属于相同簇且在 C∗C^*C∗ 中也隶属于相同簇的样本对,…
由于每个样本对 (xi,xj)(i<j)(x_i,x_j)(i<j)(xi,xj)(i<j) 仅能出现在一个集合中,因此有下列式子成立:
a+b+c+d=m(m−1)2a+b+c+d=\frac {m(m-1)} {2} a+b+c+d=2m(m−1)
外部指标
基于以上式子可导出下面这些常用的聚类性能度量外部指标:
- Jaccard系数(Jaccard Coefficient,简称 JC)
JC=aa+b+cJC = \frac {a} {a+b+c} JC=a+b+ca
- FM指数(Fowlkes and Mallows Index,简称 FMI)
FMI=aa+b⋅aa+cFMI = \sqrt{\frac {a} {a+b} \cdot \frac {a} {a+c}} FMI=a+ba⋅a+ca
- Rand指数(Rand Index,简称 RI)
RI=a(a+d)m(m−1)RI = \frac {a(a+d)} {m(m-1)} RI=m(m−1)a(a+d)
显然,上述性能度量的结果值均在 [0,1][0,1][0,1] 区间,值越大越好。
例1
| 聚类 CCC | 参考 C∗C^*C∗ |
|---|---|
| C1:x1,x2,x3C_1:x_1,x_2,x_3C1:x1,x2,x3 | C1∗:x1,x2,x4C_1^*:x_1,x_2,x_4C1∗:x1,x2,x4 |
| C2:x4,x5C_2:x_4,x_5C2:x4,x5 | C2∗:x3,x5C_2^*:x_3,x_5C2∗:x3,x5 |
a=∣SS∣=1(x1,x2)b=∣SD∣=3(x1,x3),(x2,x3),(x4,x5)c=∣DS∣=3(x1,x4),(x2,x4),(x3,x5)d=∣DD∣=3(x1,x5),(x2,x5),(x3,x4)\begin {aligned} a&=\vert SS \vert =1 \quad (x_1,x_2) \\ b&=\vert SD \vert =3 \quad (x_1,x_3),(x_2,x_3),(x_4,x_5) \\ c&=\vert DS \vert =3 \quad (x_1,x_4),(x_2,x_4),(x_3,x_5) \\ d&=\vert DD \vert =3 \quad (x_1,x_5),(x_2,x_5),(x_3,x_4) \end {aligned} abcd=∣SS∣=1(x1,x2)=∣SD∣=3(x1,x3),(x2,x3),(x4,x5)=∣DS∣=3(x1,x4),(x2,x4),(x3,x5)=∣DD∣=3(x1,x5),(x2,x5),(x3,x4)
JC=aa+b+c=11+3+3=17FMI=aa+b⋅aa+c=11+3⋅11+3=14RI=a(a+d)m(m−1)=RI=2(1+3)5(5−1)=25\begin {aligned} JC &= \frac {a} {a+b+c} = \frac {1} {1+3+3} = \frac {1} {7} \\ FMI &= \sqrt{\frac {a} {a+b} \cdot \frac {a} {a+c}} = \sqrt{\frac {1} {1+3} \cdot \frac {1} {1+3}} = \frac {1} {4} \\ RI &= \frac {a(a+d)} {m(m-1)} = RI = \frac {2(1+3)} {5(5-1)} = \frac {2} {5} \end {aligned} JCFMIRI=a+b+ca=1+3+31=71=a+ba⋅a+ca=1+31⋅1+31=41=m(m−1)a(a+d)=RI=5(5−1)2(1+3)=52
内部指标
考虑聚类结果的簇划分为 C={C1,C2,...,Ck}C = \{C_1,C_2,...,C_k\}C={C1,C2,...,Ck} ,定义
avg(C)=2∣C∣(∣C∣−1)∑1≤i<j≤∣C∣dist(xi,xj)avg(C) = \frac {2} {\vert C \vert (\vert C \vert -1)} \sum_{1 \leq i < j \leq \vert C \vert} dist(x_i,x_j) avg(C)=∣C∣(∣C∣−1)21≤i<j≤∣C∣∑dist(xi,xj)
其中,avg(C)avg(C)avg(C) 对应于簇 CCC 内样本间的平均距离,dist(⋅,⋅)dist(\cdot,\cdot)dist(⋅,⋅) 用于计算两个样本之间的距离。
diam(C)=max1≤i<j≤∣C∣dist(xi,xj)diam(C) = max_{1 \leq i < j \leq \vert C \vert} dist(x_i,x_j) diam(C)=max1≤i<j≤∣C∣dist(xi,xj)
diam(C)diam(C)diam(C) 对应于簇 CCC 内样本间的最远距离。
dmin(Ci,Cj)=minxi∈Ci,xj∈Cjdist(xi,xj)d_{min}(C_i,C_j) = min_{x_i \in C_i,x_j \in C_j} dist(x_i,x_j) dmin(Ci,Cj)=minxi∈Ci,xj∈Cjdist(xi,xj)
dmin(Ci,Cj)d_{min}(C_i,C_j)dmin(Ci,Cj) 对应于簇 CiC_iCi 和簇 CjC_jCj 最近样本间的距离。
dcen(Ci,Cj)=dist(μi,μj)d_{cen}(C_i,C_j) = dist(\mu_i,\mu_j) dcen(Ci,Cj)=dist(μi,μj)
dcen(Ci,Cj)d_{cen} (C_i,C_j)dcen(Ci,Cj) 对应于簇 CiC_iCi 和簇 CjC_jCj 中心点间的距离,μ\muμ 代表簇 CCC 的中心点 μ=1∣C∣∑1≤i≤∣C∣xi\mu = \frac {1} {\vert C \vert} \sum_{1 \leq i \leq \vert C \vert} x_iμ=∣C∣1∑1≤i≤∣C∣xi 。
基于以上式子可导出下面这些常用的聚类性能度量内部指标:
- DB指数(Davies-Bouldin Index,简称 DBI)
DBI=1k∑i=1kmaxj≠i(avg(Ci)+avg(Cj)dcen(Ci,Cj))DBI = \frac {1} {k} \sum_{i=1}^{k} \max \limits_{j \neq i}(\frac {avg(C_i) + avg(C_j)} {d_{cen}(C_i,C_j)}) DBI=k1i=1∑kj=imax(dcen(Ci,Cj)avg(Ci)+avg(Cj))
- Dunn指数(Dunn Index,简称DI)
DI=min1≤i≤kminj≠i(dmin(Ci,Cj)max1≤l≤kdiam(Cl))DI = \min \limits_{1 \leq i \leq k} \min \limits_{j \neq i}(\frac {d_{min}(C_i,C_j)} {max_{1 \leq l \leq k} diam(C_l)}) DI=1≤i≤kminj=imin(max1≤l≤kdiam(Cl)dmin(Ci,Cj))
显然,DBIDBIDBI 的值越小越好,而 DIDIDI 则相反,值越大越好。
例2
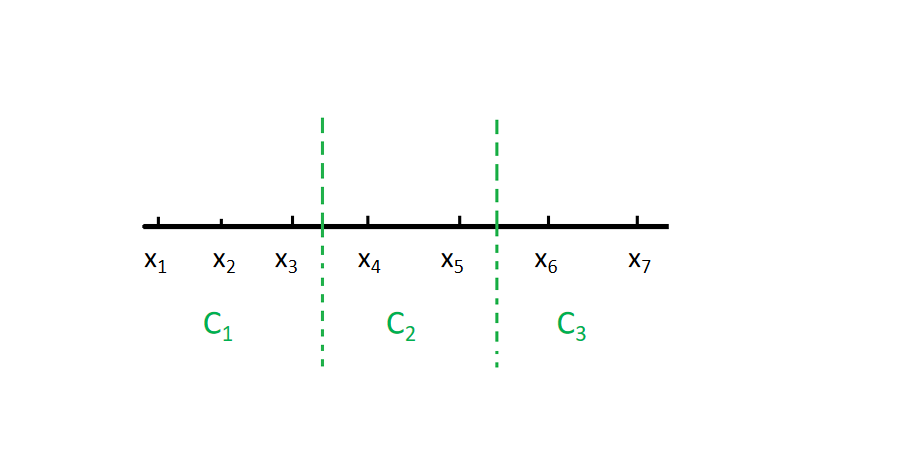
avg(C1)=23(3−1)⋅(∣x1−x2∣+∣x1−x3∣+∣x2−x3∣)avg(C2)=22(2−1)⋅(∣x4−x5∣)avg(C3)=22(2−1)⋅(∣x6−x7∣)\begin {aligned} avg(C_1) &= \frac {2} {3 (3 -1)} \cdot (\vert x_1-x_2 \vert + \vert x_1 - x_3 \vert + \vert x_2 - x_3 \vert) \\ avg(C_2) &= \frac {2} {2 (2 -1)} \cdot (\vert x_4-x_5 \vert) \\ avg(C_3) &= \frac {2} {2 (2 -1)} \cdot (\vert x_6-x_7 \vert) \end {aligned} avg(C1)avg(C2)avg(C3)=3(3−1)2⋅(∣x1−x2∣+∣x1−x3∣+∣x2−x3∣)=2(2−1)2⋅(∣x4−x5∣)=2(2−1)2⋅(∣x6−x7∣)
diam(C1)=∣x1−x3∣diam(C2)=∣x4−x5∣diam(C3)=∣x6−x7∣diam(C_1) = \vert x_1 - x_3 \vert \\ diam(C_2) = \vert x_4 - x_5 \vert \\ diam(C_3) = \vert x_6 - x_7 \vert diam(C1)=∣x1−x3∣diam(C2)=∣x4−x5∣diam(C3)=∣x6−x7∣
dmin(C1,C2)=∣x3−x4∣dmin(C2,C3)=∣x5−x6∣dmin(C1,C3)=∣x3−x6∣d_{min}(C_1,C_2) = \vert x_3 - x_4 \vert \\ d_{min}(C_2,C_3) = \vert x_5 - x_6 \vert \\ d_{min}(C_1,C_3) = \vert x_3 - x_6 \vert dmin(C1,C2)=∣x3−x4∣dmin(C2,C3)=∣x5−x6∣dmin(C1,C3)=∣x3−x6∣
μ1=x1+x2+x33μ2=x4+x52μ3=x6+x72\mu_1 = \frac {x_1 + x_2 + x_3} {3} \quad \mu_2 = \frac {x_4 + x_5} {2} \quad \mu_3 = \frac {x_6 + x_7} {2} μ1=3x1+x2+x3μ2=2x4+x5μ3=2x6+x7
dcen(C1,C2)=∣μ1−μ2∣dcen(C2,C3)=∣μ2−μ3∣dcen(C1,C3)=∣μ1−μ3∣d_{cen}(C_1,C_2) = \vert \mu_1-\mu_2 \vert \\ d_{cen}(C_2,C_3) = \vert \mu_2-\mu_3 \vert \\ d_{cen}(C_1,C_3) = \vert \mu_1-\mu_3 \vert dcen(C1,C2)=∣μ1−μ2∣dcen(C2,C3)=∣μ2−μ3∣dcen(C1,C3)=∣μ1−μ3∣
