5. 自动求导
5.1 向量链式法则

① 例子1是一个线性回归的例子,如下图所示。


5.2 自动求导

5.3 计算图
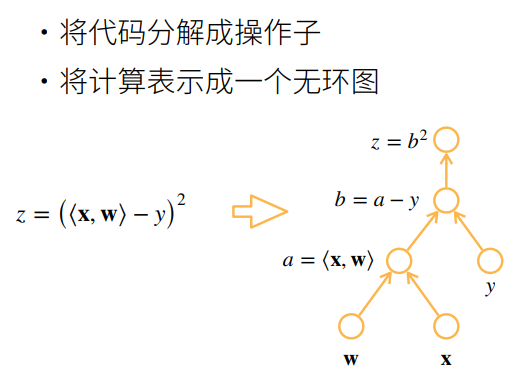


5.4 两种模型


① b是之前计算的结果,是一个已知的值。
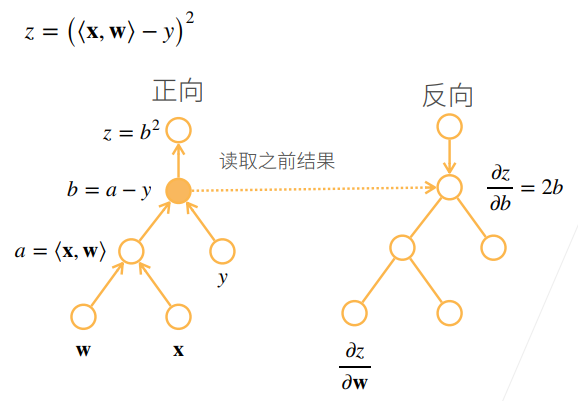



5.5 复杂度

5.6 自动求导
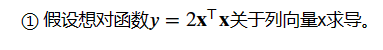
import torch
x = torch.arange(4.0)
x结果:

② 在外面计算y关于x的梯度之前,需要一个地方来存储梯度。
import torch
x = torch.arange(4.0)
x.requires_grad_(True) # 等价于 x = torch.arange(4.0,requires_grad=True)
print(x.grad) # 默认为None结果:(两种写法)

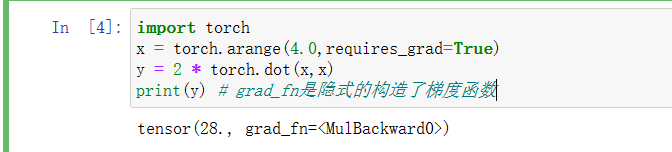
③ 现在计算y。
import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
print(y) # grad_fn是隐式的构造了梯度函数结果:
④ 通过调用反向传播函数来自动计算y关于x每个分量的梯度。
import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward() # 反向传播后会有梯度计算出来
print(x.grad) # 访问导数,即访问梯度
print(x.grad == 4 * x) # 4 * x 是 2 * x * x 的导数结果:

⑤ 计算x的另一个函数。
import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward()
# 默认情况下,PyTorch会累积梯度,需要清除之前的值
x.grad.zero_() # y.backward() 后才能产生梯度,才能梯度清零,没有反向传播,无法梯度清零
y = x.sum() # 这里的y是一个标量,sum函数其实就是x_1+x_2+...x_n,求偏导自然是全1啊
y.backward()
print(x.grad)结果:

⑥ 在深度学习中,目的不是计算微分矩阵,而是批量中每个样本单独计算的偏导数之和。
import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward()
# 默认情况下,PyTorch会累积梯度,需要清除之前的值
# 对非标量调用 'backward' 需要传入一个 'gradient' 参数,该参数指定微分函数
x.grad.zero_()
y = x * x # 这里的y不是一个标量,这是一个向量
print(y)
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward() # y.sum()后就讲向量转为标量了,对标量求导
x.grad结果:

⑦ 将某些计算移动到记录的计算图之外。
import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward()
x.grad.zero_()
y = x * x
print(y)
u = y.detach() # y.detach把y当作一个常数,而不是关于x的一个函数
print(y.detach())
print(u)
z = u * x
z.sum().backward()
x.grad == u结果:

import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward()
x.grad.zero_()
y = x * x # 这里的y是关于x的函数
x.grad.zero_()
y.sum().backward()
x.grad == 2 * x结果:

⑧ 即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数调用),仍然可以计算得到的变量的梯度。
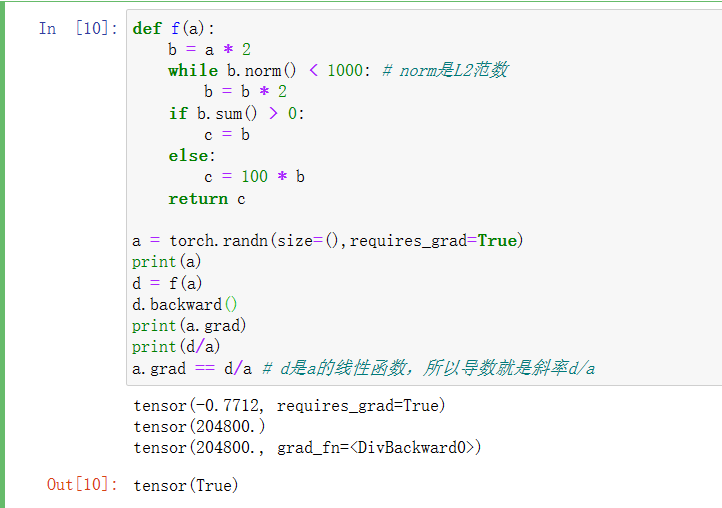
def f(a):b = a * 2while b.norm() < 1000: # norm是L2范数b = b * 2if b.sum() > 0:c = belse:c = 100 * breturn ca = torch.randn(size=(),requires_grad=True)
print(a)
d = f(a)
d.backward()
print(a.grad)
print(d/a)
a.grad == d/a # d是a的线性函数,所以导数就是斜率d/a结果: