线性代数的学习和整理18:矩阵的秩的各种定理, 秩和维度(未完成)
目录
1 矩阵的秩
矩阵的秩
2 求秩的方法
矩阵的维度=秩
矩阵的维度
向量的模,矩阵的模-没有把,难道是面积?
矩阵的平直概念
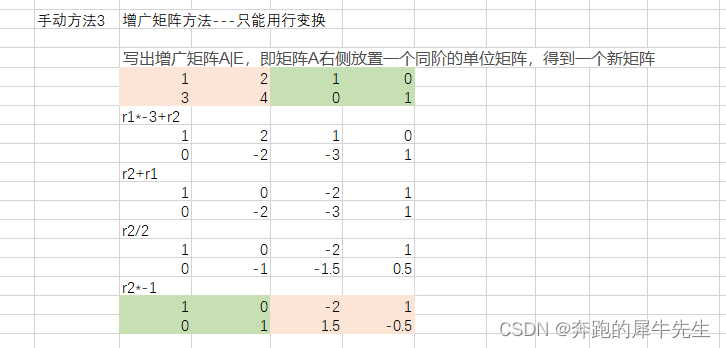
5 矩阵的初等变换(矩阵等价概念的引出)
1 为什么要引入矩阵的“秩” 这个概念?先得从这样一个现象说起
Ax=y
如果A是2维的向量/矩阵,定义域为维,那么输出的内容(值域)只能是0维,1维和2维
1 矩阵的秩
行秩
列秩
满秩
矩阵的秩
- (a1,a2)是2维的
- (a1,a2,a3)是3维的
- (a1,a2,a3... ... an)是n维的
2 求秩的方法
行列式方法
线性变换方法
化简矩阵
3.2.3 秩的性质
满秩=有逆矩阵
矩阵的维度=秩
矩阵的维度
向量的模,矩阵的模-没有把,难道是面积?
矩阵的平直概念
即矩阵需要时线性增长的意思把
比如矩阵10,10个矩阵不能缩小为90,而必须是100
5 矩阵的初等变换(矩阵等价概念的引出)
- 如果两个矩阵,经过有限次的初等变化可以相等,那么这2个矩阵是等价的
- 矩阵的初等行变换与初等列变换合称为矩阵的初等变换。
- 矩阵的初等行变换
- 交换矩阵的两行
- 以一个非零数k乘矩阵的某一行所有元素
- 把矩阵的某一行所有元素乘以一个数k后加到另一行对应的元素
- 矩阵的初等列变换
- 交换矩阵的两列
- 以一个非零数k乘矩阵的某一列所有元素
- 把矩阵的某一列所有元素乘以一个数k后加到另一列对应的元素
向量的变换,两种方法
基不变,会改变坐标(同时形状也可能改变)
基便哈/替代了,坐标不变(同时形状也不能改变)
