Leetcode107. 二叉树的层序遍历 II
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你二叉树的根节点
root,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
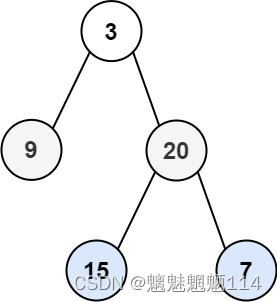
输入:root = [3,9,20,null,null,15,7] 输出:[[15,7],[9,20],[3]]
这道题和Leetcode102的基础层序遍历唯一的不同点是,每次for循环结束后,加入列表的结果,需要到最前面,res.add(0,list);和锯齿形层序遍历方法一样
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<List<Integer>> levelOrderBottom(TreeNode root) {List<List<Integer>> res = new ArrayList<>();if(root == null){return res;}Queue<TreeNode> q = new LinkedList<>();q.offer(root);while(!q.isEmpty()) {int size = q.size();List<Integer> list = new ArrayList<>();for(int i = 0; i < size; i++) {TreeNode node = q.poll();list.add(node.val);if(node.left != null){q.offer(node.left);}if(node.right != null){q.offer(node.right);}}//每次插入到最前面,倒序的层序遍历,就会实现res.add(0,list);}return res;}
}