数据结构体--5.0图
目录
一、定义
二、图的顶点与边之间的关系
三、图的顶点与边之间的关系
四、连通图
五、连通图的生成树定义
一、定义
图(Graph)是由顶点的又穷非空集合合顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V表示图G中定点的集合,E是图G中边的集合。
——线性表中我们把数据元素叫元素,树中叫结点,在图中数据元素我们则称之为定点(Vertex)。
——线性表可以没有数据元素,称为空表,树中可以没有结点,叫做空树,而图中的定点集合是有穷非空的。(国外是允许空的)
——线性表中,相邻的数据元素之间具有线性关系,数据结构中,相邻两层的结点具有层次关系,而图结构中,任意两个顶点之间都可能有关系,定点之间的逻辑关系用边来表示,边集是可以为空的。
1、无向边:若顶点Vi到Vj之间的边没有方向,则称这条边为无向边(Edge),用无序偶(Vi,Vj)来表示。

上图G1是一个无向图,G1={V1,E1},其中
——V1 = {A,B,C,D}
——E1 = {(A,C),(B,C),(C,D),(D,A),(A,C)}
2、有向边:若从定点Vi到Vj的边有方向,则称这条边为有向边,也成为弧(Arc),用有序偶<vi,Vj>来表示,Vi称为弧尾,Vj称为弧头。
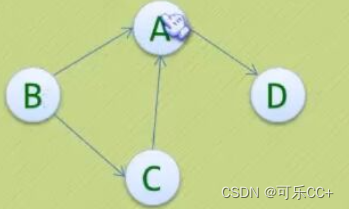
上图G2是一个有向图,G2={V2,E2},其中
——V2 = {A,B,C,D}
——E2 = {<B,A>,<B,C>,<C,A>,<A,D>}
二、图的顶点与边之间的关系
1、对于无向图G=(V,E),如果边(V1,V2)∈E,则称顶点V1和V2互为邻接点(Adjacent),即V1和V2相邻接。边(V1,V2)依附(incident)于顶点V1和V2,或者说边(V1,V2)与顶点V1和V2相关联。
2、顶点V的度(Degree)是和V相关联的边的数目,记为TD(V),如下图,顶点A与B互为邻接点,bian(A,B)依附于顶点A与B上,顶点A的度为3.

三、图的顶点与边之间的关系
1、对于有向图G=(V,E),如果边<V1,V2>∈E,则称顶点V1邻接到顶点V2,顶点V2邻接自顶点V1。
2、以顶点V为头的弧的数目称为V的入度(InDegree),记为ID(V),以V为尾的弧的数目称为V
的出度(OutDegree),记为OD(V),因此顶点V的度为TD(V)=ID(V)+OD(V)。
3、下图顶点A的入度是2,出度是1,所以顶点A的度是3。

四、连通图
1、在无向图G中,如果从顶点V1到顶点V2有路径,则称V1和V2是连通图,弱国对于图中任意两个顶点Vi和Vj都是连同的,则称G是连通图(ConnectedGraph)。
2、无向图中的极大连通子图称为连通分量。
3、注意:
——首先要是子图,并且子图是要连通的;
——连通子图含有极大顶点数;
——具有极大顶点数的连通子图包含依附于这些顶点的所有边。
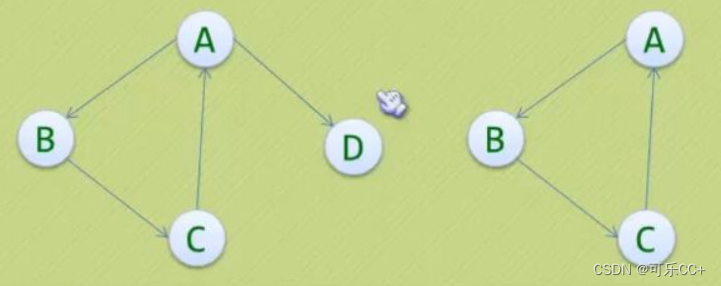
4、在有向图G中,如果对于每一对Vi到V都存在路径,则称G是强连通图。
5、有向图中的极大强连通子图称为有向图的强连通分量。
如下,左侧不是,右侧是
五、连通图的生成树定义
所谓的一个连通图的生成树是一个极小的连通子图,它含有图中全部的n个顶点,但只有足以构成一棵树的n-1跳边。
