机器学习基础之《分类算法(5)—朴素贝叶斯算法原理》
一、朴素贝叶斯算法
1、什么是朴素贝叶斯分类方法
之前用KNN算法,分类完直接有个结果,但是朴素贝叶斯分完之后会出现一些概率值,比如:
这六个类别,它都有一定的可能性
再比如,对文章进行分类: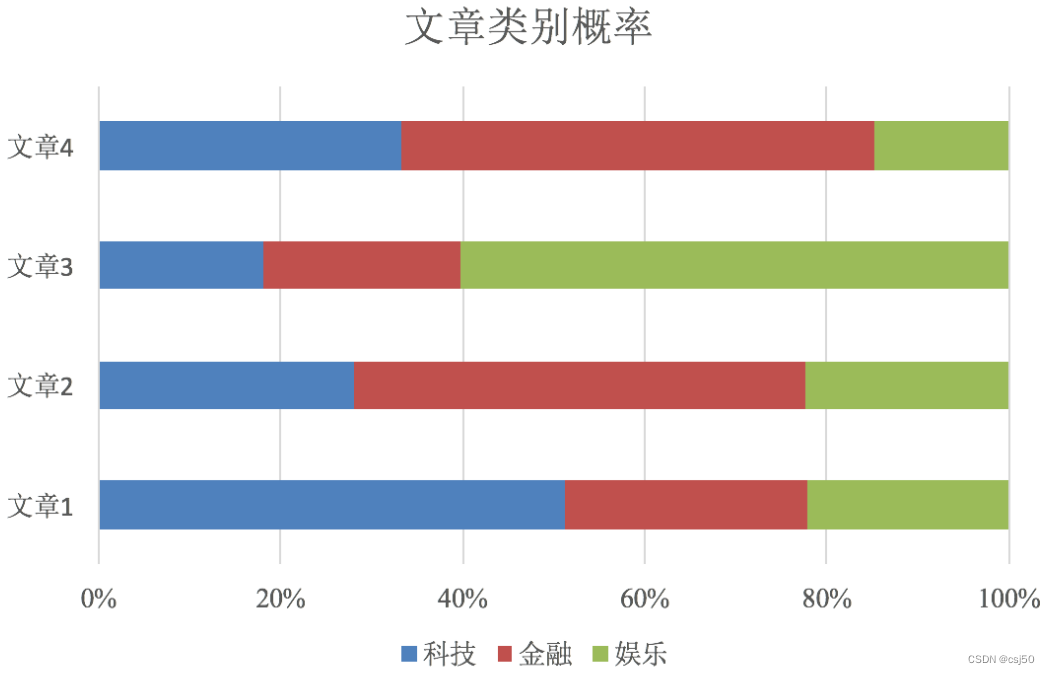
分类为三个类别,对每个样本用朴素贝叶斯分类之后,会得到这样的结果,会取概率比较大的作为最终的结果
二、概率基础
1、概率(probability)定义
概率定义为一件事情发生的可能性
比如:扔出一个硬币,结果头朝上概率是多少
2、取值范围
P(X):取值在[0, 1]
如果取值为0,是不可能事件。如果取值为1,是必然事件
3、女神是否喜欢计算案例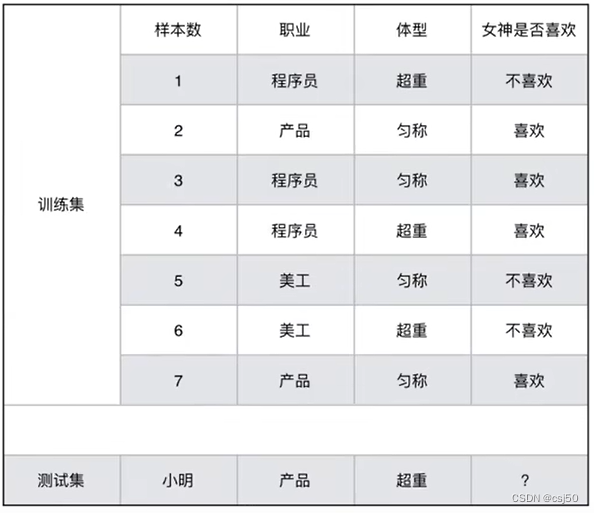
已知小明是产品经理,体重超重,是否会被女神喜欢?
特征有两个,职业和体型。目标值就是是否会被女神喜欢,是个二分类问题
4、问题
(1)女神喜欢的概率?
样本有7个,女神喜欢有4个
p(喜欢) = 4/7
(2)职业是程序员并且体型匀称的概率?
P(程序员, 匀称) = 1/7
--联合概率
(3)在女神喜欢的条件下,职业是程序员的概率?
P(程序员 | 喜欢) = 2/4
--条件概率
(4)在女神喜欢的条件下,职业是程序员,体重是超重的概率?
P(程序员, 超重 | 喜欢) = 1/4
--既符合条件概率,也符合联合概率
三、联合概率、条件概率与相互独立
1、联合概率:包含多个条件,且所有条件同时成立的概率
记作:P(A,B)
特性:P(A,B) = P(A)P(B)
例如:P(程序员, 匀称),P(程序员, 超重|喜欢)
2、条件概率:就是事件A在另外一个事件B已经发生条件下的发生概率
记作:P(A|B)
特性:P(A1,A2|B) = P(A1|B)P(A2|B)
例如:P(程序员|喜欢),P(程序员, 超重|喜欢)
3、相互独立:如果P(A,B) = P(A)P(B),则称事件A与事件B相互独立
例子:
在女神是否喜欢数据当中,程序员和匀称是否相互独立?
P(程序员, 匀称) = 1/7
P(程序员) = 3/7
P(匀称) = 4/7
所以程序员和匀称不是相互独立的
4、已知小明是产品经理,体重超重,是否会被女神喜欢?
目标是求:P(喜欢|产品, 超重) = ?
这时候就要用到贝叶斯公式
四、贝叶斯公式
1、公式
2、解决小明的问题
分子:P(产品, 超重|喜欢) * P(喜欢)
分母:P(产品, 超重)
什么是朴素:加上了假设,特征与特征之间是相互独立的
P(产品, 超重) = P(产品) * P(超重)
上式中,P(产品, 超重|喜欢)和P(产品, 超重)的结果均为0,导致无法计算结果。这是因为我们的样本量太少了,不具有代表性,本来现实生活中,肯定是存在职业是产品经理并且体重超重的人的,P(产品, 超重)不可能为0;而且事件“职业是产品经理”和事件“体重超重”通常被认为是相互独立的事件
而朴素贝叶斯可以帮助我们解决这个问题
朴素贝叶斯,简单理解,就是假定了特征与特征之间相互独立的贝叶斯公式
也就是说,朴素贝叶斯,之所以朴素,就在于假定了特征与特征相互独立
所以,思考题如果按照朴素贝叶斯的思路来解决,就可以是:
P(产品, 超重) = P(产品) * P(超重) = 2/7 * 3/7 = 6/49
P(产品, 超重|喜欢) = P(产品|喜欢) * P(超重|喜欢) = 1/2 * 1/4 = 1/8
