当前位置：首页 > news >正文

【数据结构】回溯算法公式化解题 leetcode经典题目带刷：全排列、组合、子集

news 2025/7/30 23:35:32

回溯算法

一、什么是回溯算法

回溯算法（Backtracking Algorithm）是一种解决组合问题、排列问题、选择问题等一类问题的常用算法。它通过尝试所有可能的选择来找到问题的解，当发现当前选择不符合要求时，就回溯到之前的状态，然后尝试其他的选择。

1、基本思想：

从问题的起始点开始，进行尝试，每次选择一个可能的路径。
如果发现当前选择无法达到解决问题的目标，就回退到上一个状态，尝试其他的选择。
不断地重复上述过程，直到找到解决问题的路径，或者遍历完所有可能的选择。

2、一般步骤：

确定问题的解空间和约束条件。
从解空间中选择一个可能的选择，进入下一步。
判断当前选择是否符合约束条件，如果符合，继续深入尝试下一步；如果不符合，回退到上一步。
重复上述步骤，直到找到解，或者遍历完所有可能的选择。

二、题目带练

1、全排列

题目地址
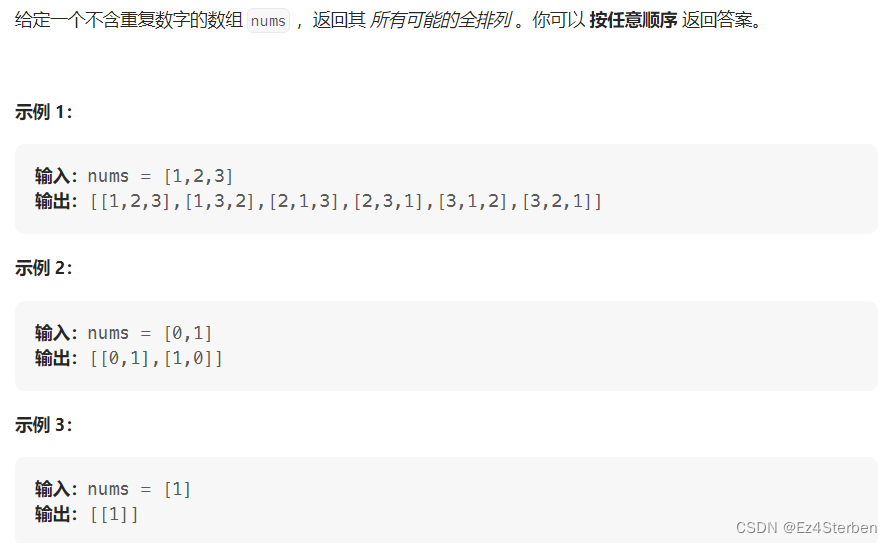
在这里插入图片描述
分析：
看到这道题的描述，不难想到，如果我们要找出所有的排列方式，就要遍历n次数组，每次选择一个不重复元素排列在上次循环选择的元素后面，那这就出现了一个问题：怎么对一个数组遍历n次？

显然这是不太可能实现的，因为n是不确定的，但是我们可以换一种思路，通过深度来代表遍历次数，也就是我们常说的回溯算法。

根据题意，我们应当设递归出口为 当前递归的深度 == 数组的长度if(depth == nums.length)，同时保存当前的排列方式到集合中。ans.add(new ArrayList<>(path));每次递归的过程中我们需要遍历一次数组for(int i = 0; i < nums.length; i++)，判断当前的元素是否被使用过if(used[i])，如果没被使用那么就将其记录下来，并且标记为使用过，继续进入递归path.add(nums[i]); used[i] = true;。当这次递归结束时dfs(nums,depth + 1,used);，撤销当前元素的使用标记，并且移除记录的集合。path.remove(path.size() - 1); used[i] = false;

效果就是调用方法后，先选择元素1path.add(nums[0]); used[0] = true;，再次调用方法记录深度+1dfs(nums,depth + 1,used);，此时发现1已经被选择过了，开始选择2path.add(nums[1]); used[1] = true;，调用递归，深度+1dfs(nums,depth + 1,used);，同理1,2被标记为使用过的元素，继续选择3path.add(nums[2]); used[2] = true;，然后递归结束。这里会退回到深度为2的那次选择，因为2之后还有别的元素可以选择，选择3后发现只有2可以选了，首选项为1的递归结束，依次类推得到所有排列方式。
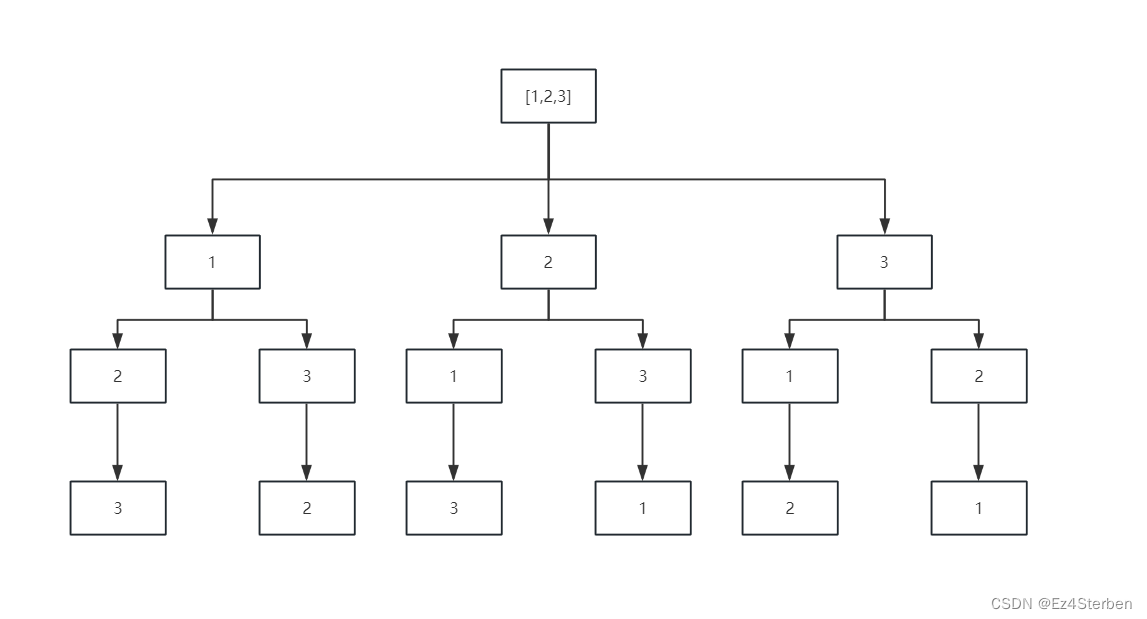
在这里插入图片描述

代码如下：

class Solution {public List<List<Integer>> ans = new ArrayList<>();public List<Integer> path = new ArrayList<>();public List<List<Integer>> permute(int[] nums) {boolean[] used = new boolean[nums.length];dfs(nums,0,used);return ans;}public void dfs(int[] nums,int depth,boolean[] used){if(depth == nums.length){ans.add(new ArrayList<>(path));return;}for(int i = 0; i < nums.length; i++){if(used[i]){continue;}path.add(nums[i]);used[i] = true;dfs(nums,depth + 1,used);path.remove(path.size() - 1);used[i] = false;}}
}

2、组合

题目地址
在这里插入图片描述
分析：

这道题与全排列的区别在于，全排列需要全部选择，而这道题不一定要全部选择，并且每个组合只能有一次，所以面对这道题，我们不能按照和之前同样的思路去解，因为无法排除同样组合的组合顺序问题。

那么我们要如何作出改动呢？

其实很简单，我们只需要让每次循环的起始值变为当前的深度即可，同时也不需要判断是否使用过了，因为我们只会向后找，不会从前开始往后找了。

class Solution {List<Integer> temp = new ArrayList<Integer>();List<List<Integer>> ans = new ArrayList<List<Integer>>();public List<List<Integer>> combine(int n, int k) {dfs(1, n, k);return ans;}public void dfs(int depth, int n, int k) {if (temp.size() == k) {ans.add(new ArrayList<Integer>(temp));return;}for(int i = depth;i <= n;i++){temp.add(i);dfs(i + 1, n, k);temp.remove(temp.size() - 1);}}
}

3、子集

题目地址
在这里插入图片描述
分析：

大家看这道题可能会发现，是不是和组合有点相似？区别在哪呢，区别在于子集的选择长度不一定是n，而是[0,n]。

其实我们只需要每次回溯都记录一次结果就好了。

class Solution {List<Integer> list = new ArrayList<>();List<List<Integer>> result = new ArrayList<>();public List<List<Integer>> subsets(int[] nums) {dfs(0,nums);return result;}public void dfs(int current, int[] nums){result.add(new ArrayList<>(list));if(current == nums.length){return;}for(int i = current; i < nums.length; i++){list.add(nums[i]);dfs(i + 1, nums);list.remove(list.size() - 1);}}
}