Java代码使用最小二乘法实现线性回归预测
最小二乘法
简介
最小二乘法是一种在误差估计、不确定度、系统辨识及预测、预报等数据处理诸多学科领域得到广泛应用的数学工具。
它通过最小化误差(真实目标对象与拟合目标对象的差)的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小
最小二乘法也是一种优化方法,求得目标函数的最优值。并且也可以用于曲线拟合,来解决回归问题。回归学习最常用的损失函数是平方损失函数,在此情况下,回归问题可以著名的最小二乘法来解决。
简而言之,最小二乘法同梯度下降类似,都是一种求解无约束最优化问题的常用方法,并且也可以用于曲线拟合,来解决回归问题。
图解
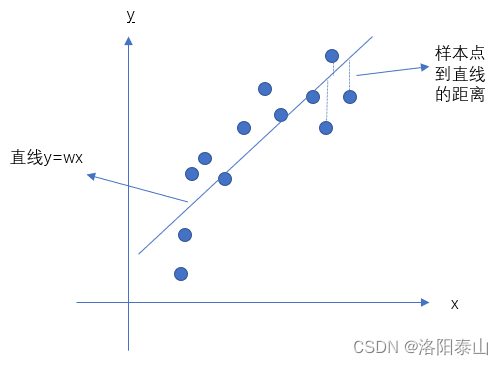
最小二乘求解,即给定一组x和y的样本数据,计算出一条斜线,距离每个样本的y的距离的平均值最小,如下图(这个以水平线为例):
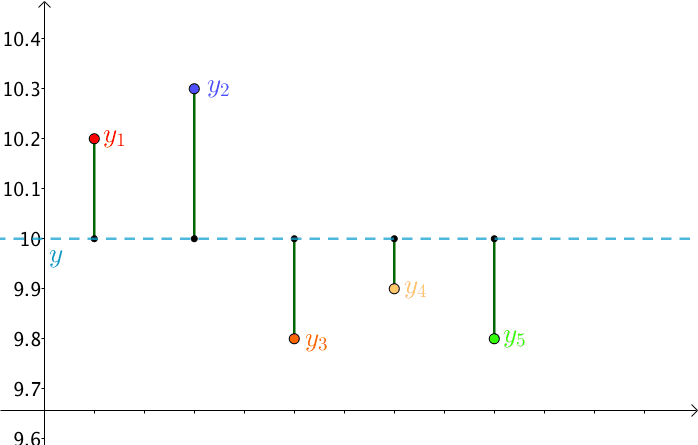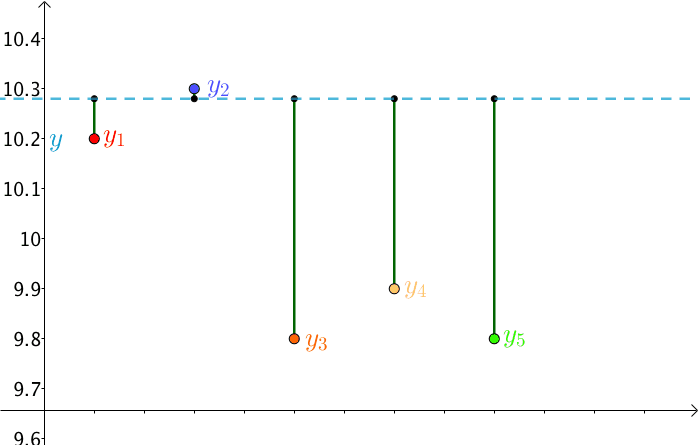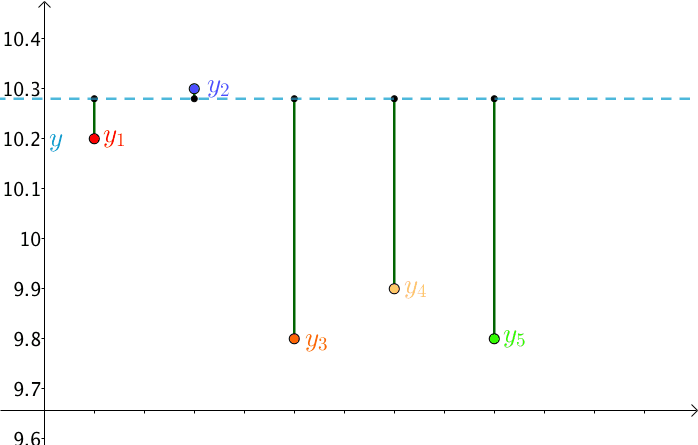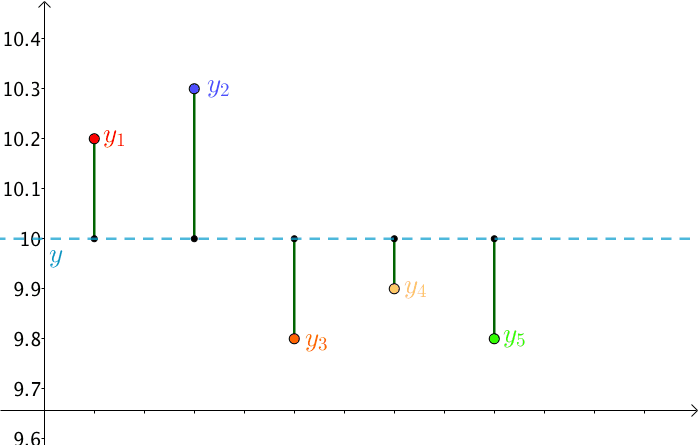
公式
普通最小二乘法一般形式可以写成(字母盖小帽表示估计值,具体参考应用概率统计):
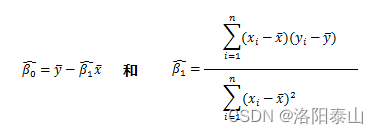
即:

代码
import java.util.HashMap;
import java.util.Map;/*** 线性回归* @author tarzan*/
public class LineRegression {/** 直线斜率 */private static double k;/** 截距 */private static double b;/*** 最小二乘法* @param xs* @param ys* @return y = kx + b, r*/public Map<String, Double> leastSquareMethod(double[] xs, double[] ys) {if(0 == xs.length || 0 == ys.length || xs.length != ys.length) {throw new RuntimeException();}// x平方差和double Sx2 = varianceSum(xs);// y平方差和double Sy2 = varianceSum(ys);// xy协方差和double Sxy = covarianceSum(xs, ys);double xAvg = arraySum(xs) / xs.length;double yAvg = arraySum(ys) / ys.length;k = Sxy / Sx2;b = yAvg - k * xAvg;//拟合度double r = Sxy / Math.sqrt(Sx2 * Sy2);Map<String, Double> result = new HashMap<>(5);result.put("k", k);result.put("b", b);result.put("r", r);return result;}/*** 根据x值预测y值** @param x x值* @return y值*/public double getY(double x) {return k*x+b;}/*** 根据y值预测x值** @param y y值* @return x值*/public double getX(double y) {return (y-b)/k;}/*** 计算方差和* @param xs* @return*/private double varianceSum(double[] xs) {double xAvg = arraySum(xs) / xs.length;return arraySqSum(arrayMinus(xs, xAvg));}/*** 计算协方差和* @param xs* @param ys* @return*/private double covarianceSum(double[] xs, double[] ys) {double xAvg = arraySum(xs) / xs.length;double yAvg = arraySum(ys) / ys.length;return arrayMulSum(arrayMinus(xs, xAvg), arrayMinus(ys, yAvg));}/*** 数组减常数* @param xs* @param x* @return*/private double[] arrayMinus(double[] xs, double x) {int n = xs.length;double[] result = new double[n];for(int i = 0; i < n; i++) {result[i] = xs[i] - x;}return result;}/*** 数组求和* @param xs* @return*/private double arraySum(double[] xs) {double s = 0 ;for( double x : xs ) {s = s + x ;}return s ;}/*** 数组平方求和* @param xs* @return*/private double arraySqSum(double[] xs) {double s = 0 ;for( double x : xs ) {s = s + Math.pow(x, 2);}return s ;}/*** 数组对应元素相乘求和* @param xs* @return*/private double arrayMulSum(double[] xs, double[] ys) {double s = 0 ;for( int i = 0 ; i < xs.length ; i++ ){s = s + xs[i] * ys[i] ;}return s ;}public static void main(String[] args) {double[] xData = new double[]{1, 2, 3, 4,5,6,7,8,9,10,11,12};double[] yData = new double[]{4200,4300,4000,4400,5000,4700,5300,4900,5400,5700,6300,6000};LineRegression lineRegression= new LineRegression();System.out.println(lineRegression.leastSquareMethod(xData, yData)); //预测System.out.println(lineRegression.getY(10d));}
}
代码中的k为线性直线的斜率,b为截距,r代表计算结果的直线拟合度。
当r = 1时称为完美拟合,当r =0 时称为糟糕拟合,
事实上,R2不因y 或x 的单位变化而变化。
零条件均值,指给定解释变量的任何值,误差的期望值为零。换言之,即 E(u|x)=0。
测试
idea中运行上面代码的主方法,控制台输出为:
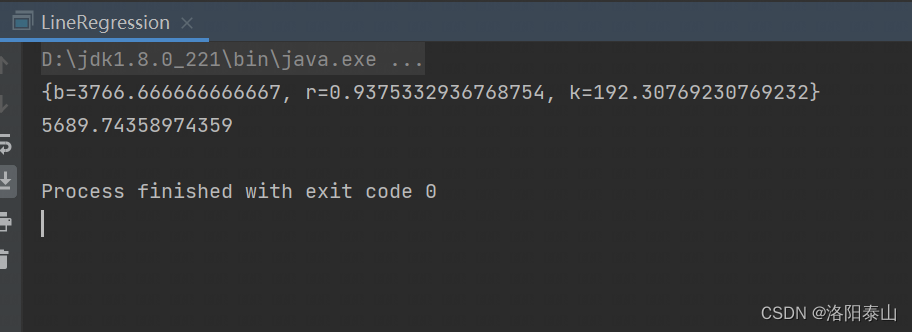
r的值接近于1,说明拟合度高。 测试x=10 时,输出结果5689.7与真实值误差约为11。
最小二乘法线性回测,常用股票、公司未来营收的预测。有着广泛的应用。
文章还有没讲清楚的地方,或为你有疑问的地方,欢迎评论区留言!!!
