二叉树OJ(一)二叉树的最大深度 二叉搜索树与双向链表 对称的二叉树
二叉树的最大深度
二叉树中和为某一值的路径(一)
二叉搜索树与双向链表
对称的二叉树
二叉树的最大深度
描述
求给定二叉树的最大深度,
深度是指树的根节点到任一叶子节点路径上节点的数量。
最大深度是所有叶子节点的深度的最大值。
(注:叶子节点是指没有子节点的节点。)
【递归】
class Solution {
public:int maxDepth(TreeNode* root) {// write code hereif(root==nullptr)return 0;int left = maxDepth(root->left);int right = maxDepth(root->right);return left>right?left+1:right+1;}
};【非递归】层序遍历(使用队列存储结点)
class Solution {
public:int maxDepth(TreeNode* root) {// write code hereif(root == nullptr)return 0;int res = 0;queue<TreeNode*> q;q.push(root);while(!q.empty()){int size = q.size();while(size--){TreeNode* cur = q.front();q.pop();if(cur->left) q.push(cur->left);if(cur->right) q.push(cur->right);}res++;}return res;}
};
二叉树中和为某一值的路径(一)
描述
给定一个二叉树root和一个值 sum ,判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。
1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
2.叶子节点是指没有子节点的节点
3.路径只能从父节点到子节点,不能从子节点到父节点
4.总节点数目为n
例如:
给出如下的二叉树, sum=22 sum=22,
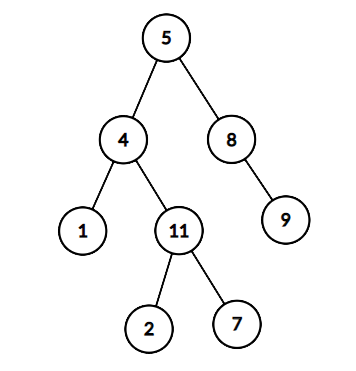
返回true,因为存在一条路径 5→4→11→25→4→11→2的节点值之和为 22
class Solution {
public:bool flag = false;void dfs(TreeNode* root, int sum){if(root==nullptr)return;sum-=root->val;if(sum==0 && root->left==nullptr && root->right==nullptr){flag = true; // 如果为根节点并且sum==0那么存在路径return;}dfs(root->left, sum);dfs(root->right, sum);}bool hasPathSum(TreeNode* root, int sum) {dfs(root, sum);return flag;}
};
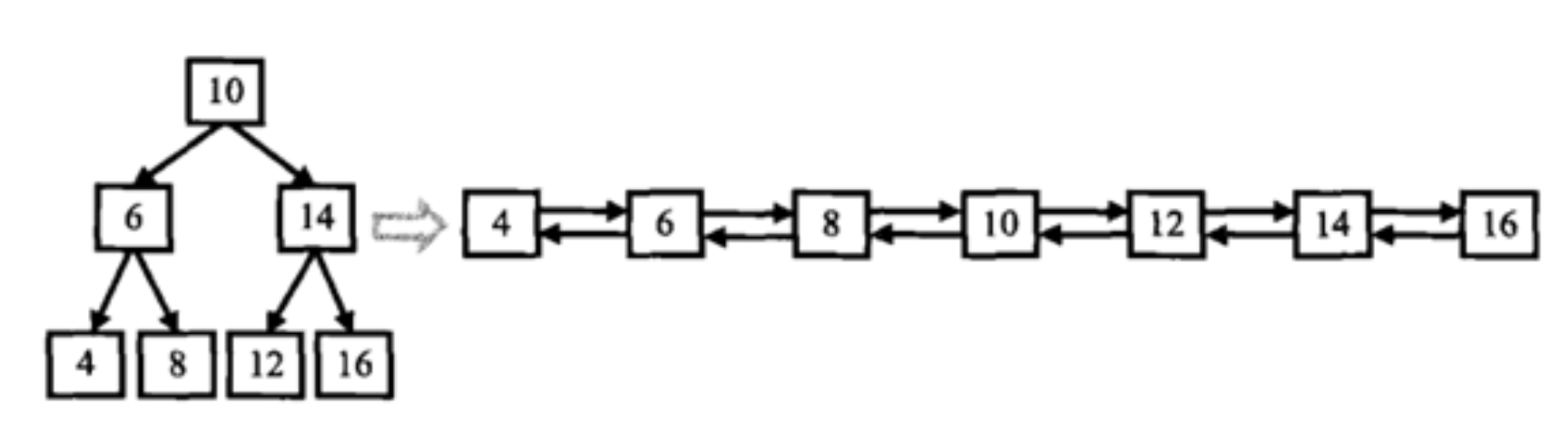
二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。如下图所示
数据范围:输入二叉树的节点数 0≤n≤10000≤n≤1000,二叉树中每个节点的值 0≤val≤10000≤val≤1000
要求:空间复杂度O(1)O(1)(即在原树上操作),时间复杂度 O(n)O(n)注意:
1.要求不能创建任何新的结点,只能调整树中结点指针的指向。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode,有左右指针,其实可以看成一个双向链表的数据结构4.你不用输出双向链表,程序会根据你的返回值自动打印输出
class Solution {
public:vector<TreeNode*> res;void Inoder(TreeNode* root){if(root == NULL)return;Inoder(root->left);res.push_back(root);Inoder(root->right);}TreeNode* Convert(TreeNode* pRootOfTree) {if(pRootOfTree==NULL)return NULL;Inoder(pRootOfTree);for(int i = 0; i < res.size()-1; ++i){res[i]->right = res[i+1];res[i+1]->left = res[i];}return res[0];}
};
对称的二叉树
描述
给定一棵二叉树,判断其是否是自身的镜像(即:是否对称)
例如: 下面这棵二叉树是对称的
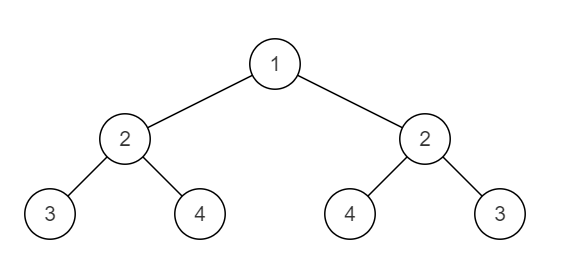
下面这棵二叉树不对称。
数据范围:节点数满足 0≤n≤10000≤n≤1000,节点上的值满足 ∣val∣≤1000∣val∣≤1000
要求:空间复杂度 O(n)O(n),时间复杂度 O(n)O(n)
备注:
你可以用递归和迭代两种方法解决这个问题
【递归解法】
class Solution {
public:bool recursion(TreeNode* p, TreeNode* q){if(p==nullptr && q==nullptr)return true;else if(p==nullptr || q==nullptr)return false;else if(q->val != p->val)return false;return recursion(p->left, q->right) && recursion(p->right, q->left);}bool isSymmetrical(TreeNode* root) {if(root==nullptr)return true;return recursion(root, root);}
};【非递归】
class Solution {
public:bool isSymmetrical(TreeNode* root) {if(root==nullptr)return true;queue<TreeNode*> q1;queue<TreeNode*> q2;q1.push(root->left);q2.push(root->right);while(!q1.empty() && !q2.empty()){TreeNode* left = q1.front();TreeNode* right = q2.front();q1.pop();q2.pop();if(left==nullptr && right==nullptr)continue;if(left==nullptr || right==nullptr || left->val != right->val)return false;q1.push(left->left);q1.push(left->right);q2.push(right->right);q2.push(right->left);}return true;}
};