LeetCode235. 二叉搜索树的最近公共祖先
235. 二叉搜索树的最近公共祖先
文章目录
- [235. 二叉搜索树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/)
- 一、题目
- 二、题解
- 方法一:递归
- 方法二:迭代
一、题目
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
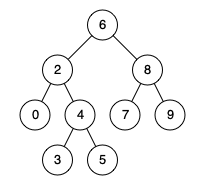
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
二、题解
方法一:递归
我们需要充分利用二叉搜索树的性质,即左子树的所有节点值都小于根节点值,右子树的所有节点值都大于根节点值。这个性质可以帮助我们有效地缩小搜索范围。
算法思路
-
首先,我们要考虑一种简单情况:如果根节点的值大于节点 p 和 q 的值,那么说明 p 和 q 位于根节点的左子树中,因为左子树的所有节点值都小于根节点值。我们可以在根节点的左子树上继续搜索 p 和 q 的最近公共祖先。
-
同样,如果根节点的值小于节点 p 和 q 的值,那么说明 p 和 q 位于根节点的右子树中,因为右子树的所有节点值都大于根节点值。我们可以在根节点的右子树上继续搜索 p 和 q 的最近公共祖先。
-
但是,如果根节点的值介于节点 p 和 q 的值之间,或者根节点的值等于其中一个节点的值,那么说明 p 和 q 分别位于根节点的左右子树中,此时根节点就是它们的最近公共祖先。
-
我们可以利用递归来实现这个过程,根据上述的思路,递归搜索左子树和右子树,最终找到最近公共祖先。
具体实现
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root == nullptr) return nullptr;if (root->val > p->val && root->val > q->val) {TreeNode* left = lowestCommonAncestor(root->left, p, q);return left;}if (root->val < p->val && root->val < q->val) {TreeNode* right = lowestCommonAncestor(root->right, p, q);return right;}return root;}
};
算法分析
时间复杂度
- 在每个递归步骤中,我们都会根据节点的值来决定是继续在左子树搜索还是在右子树搜索,所以每次递归都会剔除一半的节点。因此,算法的时间复杂度为 O(log N),其中 N 是树中节点的总数。
空间复杂度
- 递归调用栈的最大深度取决于树的高度,对于平衡的二叉搜索树,空间复杂度为 O(log N);对于不平衡的树,最坏情况下的空间复杂度为 O(N),其中 N 是树中节点的总数。
方法二:迭代
简单来说,就是把上面的递归思路用迭代方式写一遍:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {while(root){if(root->val > p->val && root->val > q->val){root = root->left;}else if(root->val < p->val && root->val < q->val){root = root->right;}else{return root;}}return root;}
};
