Codeforces Round 881 Div.3
文章目录
- 贪心:A. Sasha and Array Coloring
- 结论:B. Long Long
- 性质:C. Sum in Binary Tree
- dfs求叶子数量:D. Apple Tree
- 二分与前缀和:E. Tracking Segments
贪心:A. Sasha and Array Coloring
Problem - A - Codeforces
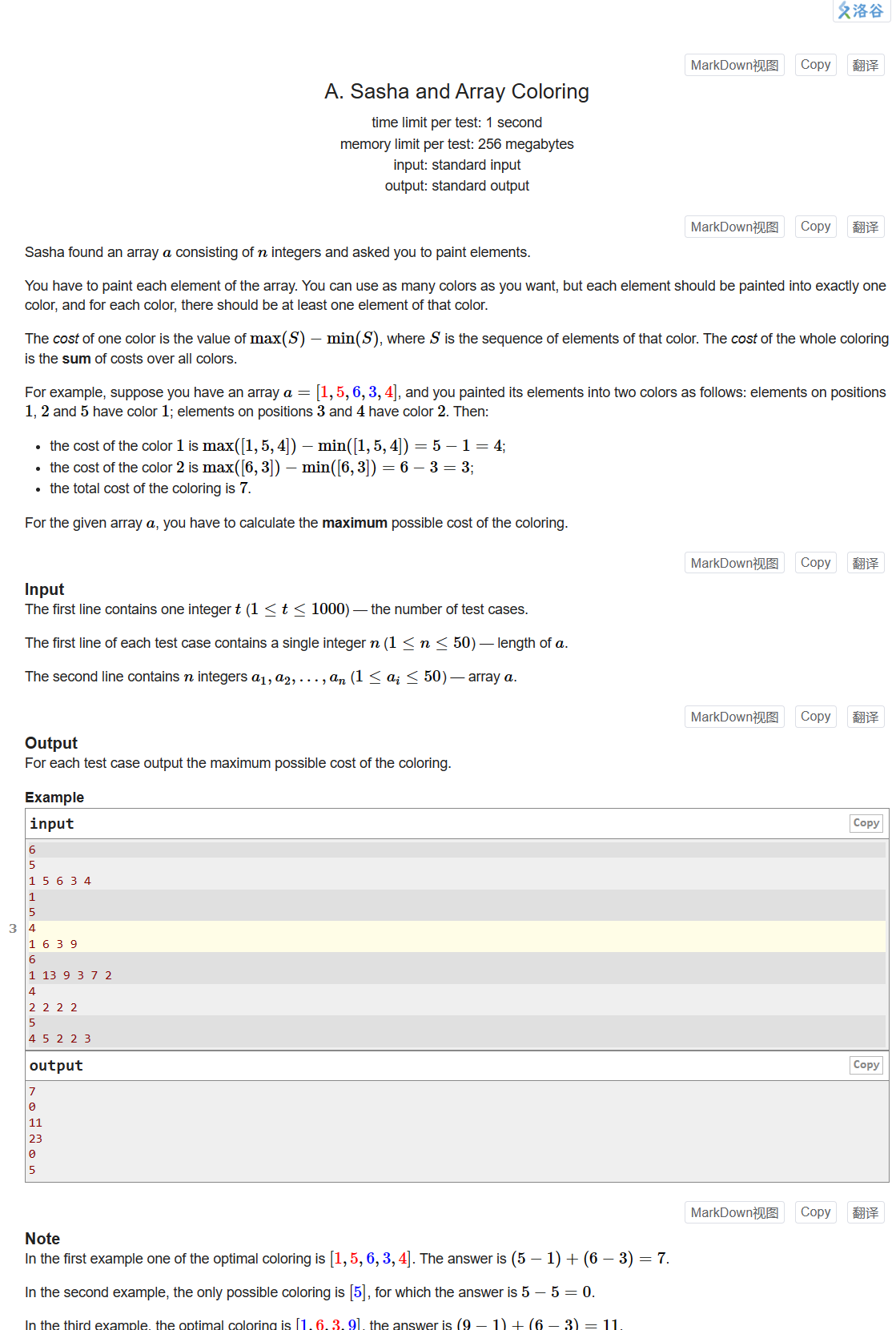
将数组中的每个数染色,同一颜色的数字中,将最大值与最小值相减得到分数,问:所有的染色方案中,总分最高是多少
显然,同一颜色的数字除了最大和最小,其他的数没有用,要使总分最高,同一颜色的数字要最少,最少为两个
将数组的最大与最小相减得到分数,再将次大与次小相减…
#include <iostream>
#include <algorithm>
using namespace std;const int N = 55;
int a[N], T;int main()
{cin >> T;while ( T -- ){int n, sum = 0;cin >> n;for (int i = 0; i < n; ++ i ) cin >> a[i];sort(a, a + n);int l = 0, r = n - 1;while (l < r){sum += (a[r] - a[l]);l ++ , r -- ;}cout << sum << endl;}return 0;
}
结论:B. Long Long

sum一定是所有数绝对值之和
结论:最少操作次数等于连续负数子段个数,所有统计连续非负的子段数量即可
#include <iostream>
#include <cmath>
using namespace std;typedef long long LL;
const int N = 2e5 + 10;
int a[N], T;int main()
{cin >> T;while ( T -- ){LL n, sum = 0, cnt = 0;cin >> n;for (int i = 0; i < n; ++ i) {cin >> a[i];sum += abs(a[i]);}for (int i = 0; i < n;){if (a[i] < 0){cnt ++ ;while (i < n && a[i] <= 0) i ++ ;}else i ++ ;}cout << sum << ' ' << cnt << endl;}return 0;
}
debug:ans要开LL,wa了4发,非负子段中可以出现0,所以a[i] < 0是不行的
性质:C. Sum in Binary Tree
Problem - C - Codeforces
[外链图片转存中…(img-XlnHbBnn-1692359176162)]
一颗完全二叉树,根节点编号为1号,问根节点到n号节点的编号之和
手写堆时,学过:孩子的编号 / 2为父亲的编号,父亲的编号 * 2,或* 2 + 1能得到左右孩子的编号
若从1开始走到n,路径是无法一次确定的。从n走到1,路径能一次确定。所以将n不断/2,就能走到根节点,过程中维护sum即可
#include <iostream>
using namespace std;typedef long long LL;int main()
{int T;cin >> T;while ( T -- ){LL sum = 0, n;cin >> n;while (n){sum += n;n /= 2;}cout << sum << endl;}return 0;
}
dfs求叶子数量:D. Apple Tree
Problem - D - Codeforces
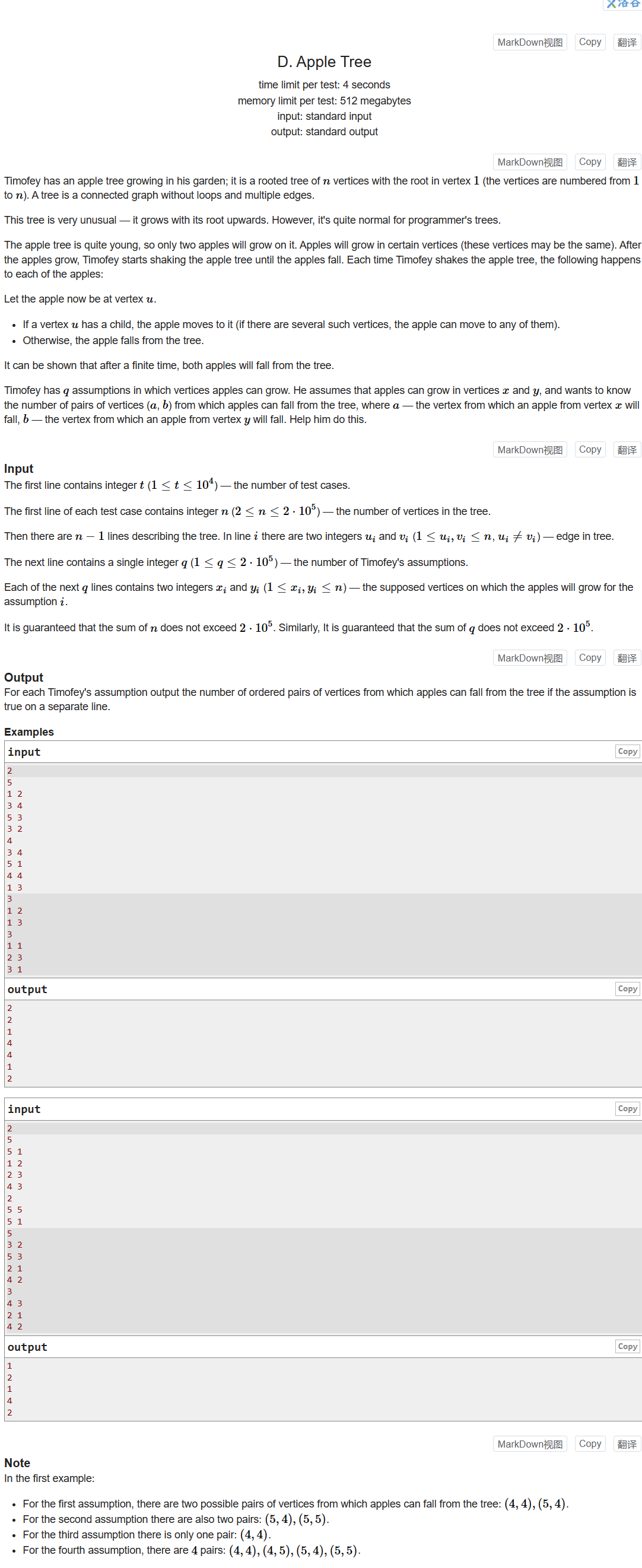
对于所有节点1~n,求以每个节点为根节点时,子树中叶子节点的数量leaf[i]
答案为leaf[x] * leaf[y]
用dfs求叶子节点的数量,有两个坑:树要建无向边,一开始我自以为是有向边,方向从根节点向下,但通过用例就能看出这是无向边
其次,无向树较难实现在线求叶子节点数量,一开始我写的是有向树,用dfs在线求叶子节点数量很好实现。但是无向树想要在线求,有一个问题,dfs会向根节点遍历,虽然能特判根节点不是叶子,但是dfs会遍历到不属于当前子树的叶子
解决方法是:用根节点开始dfs,用leaf数组保存每颗子树的叶子节点,从其他节点开始地离线求法依然是错的,只能从根节点开始求
#include <iostream>
#include <cstring>
using namespace std;typedef long long LL;
const int N = 2e5 + 10, M = 4e5 + 10;
int h[N], e[M], ne[M], idx;
int T, n, Q;
int leaf[N];void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}int dfs(int x, int fa)
{bool flag = true;int cnt = 0;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (y != fa) flag = false, leaf[x] += dfs(y, x);}if (flag) leaf[x] = 1; return leaf[x];
}int main()
{cin >> T;while ( T -- ){memset(h, -1, sizeof h);memset(leaf, 0, sizeof leaf);idx = 0;cin >> n;int x, y;for (int i = 0; i < n - 1; ++ i ){cin >> x >> y;add(x, y), add(y, x);}cin >> Q;dfs(1, -1);while ( Q -- ){cin >> x >> y;cout << (LL)leaf[x] * leaf[y] << endl;}}return 0;
}
二分与前缀和:E. Tracking Segments
Problem - E - Codeforces
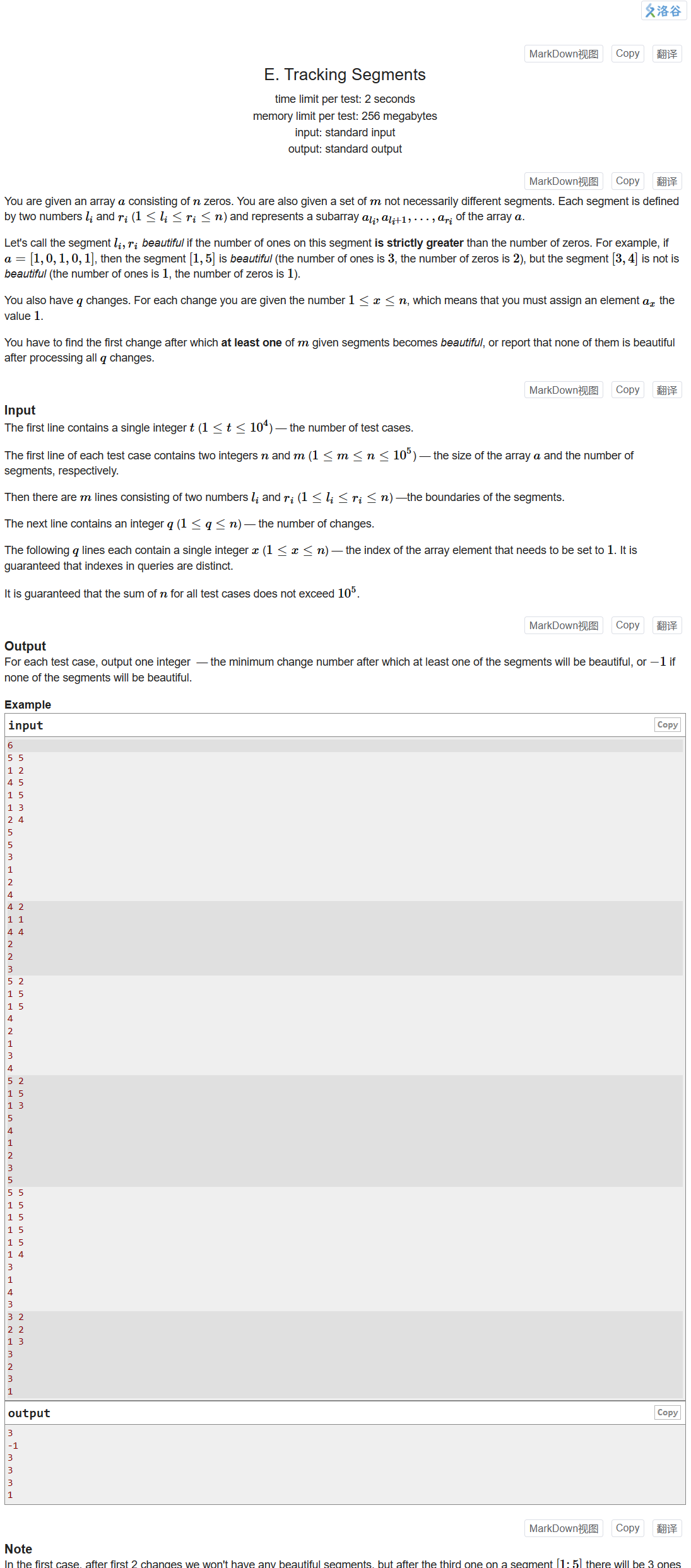
每次做二分题脑子都转不过来,要将边界问题考虑得很清楚
首先,分析题意:一个元素全为0的数组,给定m个区间与q个操作,每次操作将某个元素置为1,问第几次操作时,m个区间中至少有一个区间的1的数量大于0的数量
可以看出这题具有二段性,由于每次操作都是将0置为1,所以整个数组中1的数量随着操作次数增加。假设答案为ans,进行ans次操作后,有一个区间的1数量大于0数量。那么在之后的操作中,1的数量只增不减。所以对于第 [ a n s , m ] [ans, m] [ans,m]次操作,至少有1个区间的1数量大于0数量
而在进行第 [ 1 , a n s − 1 ] [1, ans-1] [1,ans−1]次操作时,所有区间1的数量一定小于0的数量,操作次数呈现两段性
根据操作次数 [ 1 , q ] [1, q] [1,q]的两段性,我们可以二分出两段区间的分界点,即最终答案ans
每次check时,进行mid次操作,遍历所有区间,只要有区间的1数量大于0数量,check就返回true。说明mid落在了右半段区间,r = mid。若check为false,说明mid落在左半区间,l = mid + 1
什么情况下会无解?进行了q次操作后,依然没有一个区间的1数量大于0数量,此时无解。那么无解时,会二分到哪个答案?因为操作次数的范围为 [ 1 , q ] [1, q] [1,q],所以无解时操作次数为 q + 1 q + 1 q+1
因此二分的区间需要设置为 [ 1 , q + 1 ] [1, q + 1] [1,q+1],当最后的结果为 q + 1 q + 1 q+1时,无解
用前缀和求区间中1的数量
#include <iostream>
#include <cstring>
using namespace std;const int N = 1e5 + 10;
int n, m;
int a[N], T, Q, L[N], R[N], change[N];bool check(int mid)
{for (int i = 1; i <= m; ++ i) {int ones = a[R[i]] - a[L[i] - 1];if (2 * ones > R[i] - L[i] + 1) return true;}return false;
}int main()
{cin >> T;while ( T -- ){cin >> n >> m;for (int i = 1; i <= m; ++ i ) cin >> L[i] >> R[i];cin >> Q;for (int i = 1; i <= Q; ++ i ) cin >> change[i]; int l = 0, r = Q + 1;while (l < r){int mid = l + r >> 1;memset(a, 0, sizeof a);for (int i = 1; i <= mid; ++ i ) a[change[i]] = 1;for (int i = 1; i <= n; ++ i ) a[i] += a[i - 1];if (check(mid)) r = mid;else l = mid + 1;}if (r == Q + 1) puts("-1");else cout << r << endl;}return 0;
}
debug:check要建立所有的区间,所以for循环中,i <= m,我写成了i <= mid,WA两发
i <= mid应该是枚举操作时的条件
剩下两题有些难,20号之后回来补
