【数据结构】二叉树
完全二叉树
是指所有结点度数
小于等于2的树
所以这种情况也是:
几条性质
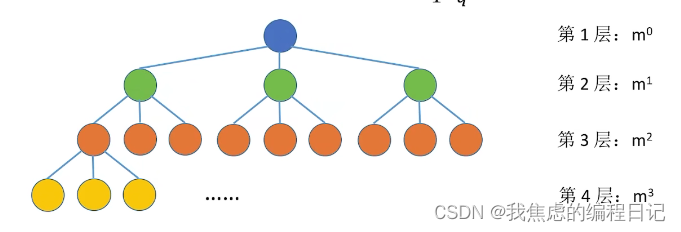
- 一个具有n个结点的
完全二叉树的深度为: log 2 ( n + 1 ) 的结果向上取整。 \\\log_{2}(n+1) \ \ 的结果向上取整。 log2(n+1) 的结果向上取整。 - 设度为0的结点个数是n0,度为1的结点个数是n1,度为2的结点个数是n2,那么n0 = n2 + 1。
推导:一棵树的所有结点个数为n0+n1+n2 —> 这棵树的边有n0+n1+n2 -1 条
这棵树的边数同时也等于n1+2*n2(度为0的能提供0条边,1的提供1条边,2的提供2条边)
那么n0+n1+n2 -1 = n1+2 *n2
可得 n0 = n2 + 1
证毕。
- 度数之和等于边数的二倍(握手定理)
- 树中结点与边的关系为结点数-边数=1
- 高度为h的二叉树至多有2h-1个结点(满二叉树)
利用等比数列求和公式算得:
将各层结点个数加起来即可。
遍历方式
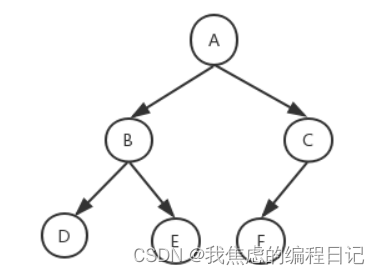
以这棵树为例: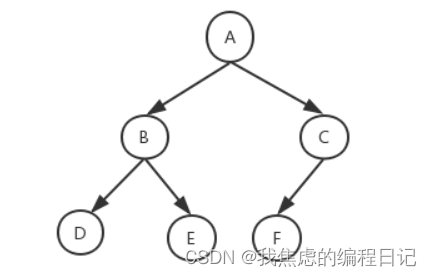
前序
所有子树按照 根左右的方式进行遍历
A B D NULL NULL E NULL NULL C F NULL NULL NULL
中序
所有子树按照 左根右 的方式进行遍历
NULL D NULL B NULL E NULL A NULL F NULL C NULL
后序
所有子树按照 左右根 的方式进行遍历
NULL NULL D NULL NULL E B NULL NULL F NULL C A
层序
所有子树按照 从上到下 从左到右 的方式进行遍历
ABCDEF