[蓝桥杯 2016 国 AC] 路径之谜

题目描述

小明冒充 $X$ 星球的骑士，进入了一个奇怪的城堡。

城堡里边什么都没有，只有方形石头铺成的地面。

假设城堡地面是 $n\times n$ 个方格。如图所示。

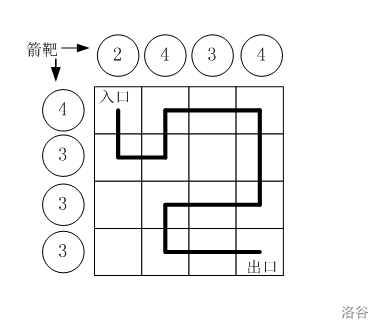
按习俗，骑士要从西北角走到东南角。

可以横向或纵向移动，但不能斜着走，也不能跳跃。

每走到一个新方格，就要向正北方和正西方各射一箭。

（城堡的西墙和北墙内各有 $n$ 个靶子）

同一个方格只允许经过一次。但不必做完所有的方格。

如果只给出靶子上箭的数目，你能推断出骑士的行走路线吗？

有时是可以的，比如如图中的例子。

本题的要求就是已知箭靶数字，求骑士的行走路径（测试数据保证路径唯一）

输入格式

第一行一个整数 $N(0<N<20)$，表示地面有 $N\times N$ 个方格。

第二行 $N$ 个整数，空格分开，表示北边的箭靶上的数字（自西向东）

第三行 $N$ 个整数，空格分开，表示西边的箭靶上的数字（自北向南）

输出格式

一行若干个整数，表示骑士路径。

为了方便表示，我们约定每个小格子用一个数字代表，从西北角开始编号 $:0,1,2,3 \cdots $。

比如，图中的方块编号为：

0  1  2  3
4  5  6  7
8  9  10 11
12 13 14 15

样例 #1

样例输入 #1

4
2 4 3 4
4 3 3 3

样例输出 #1

0 4 5 1 2 3 7 11 10 9 13 14 15

提示

时限 1 秒, 256M。蓝桥杯 2016 年第七届国赛

众所周知，蓝桥杯奖水题不水
经过两个小时的折磨，终于做出来了，网上的题解能不能先把题目过了再发。。
使用dfs，运用减枝，开四个数组来标记，然后就是dfs常规的了，但是题目各种细节，使人心力交瘁

#include<bits/stdc++.h>
using namespace std;
const int N=25;
int g[N][N];
bool vis[N][N];
int path[450];
int n,cnt,k;
bool f;
int ax[N],ay[N];
int bx[N],by[N];
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
bool check()
{for(int i=1;i<=n;i++){if(bx[i]!=ax[i]||by[i]!=ay[i])return 0;}return 1;
}void dfs(int x,int y)
{if(f) return ;if(x==n&&y==n&&check()){for(int i=0;i<cnt;i++)cout<<path[i]<<" ";f=1;return;}for(int i=0;i<4;i++){int xxx=x+dx[i],yyy=y+dy[i];if(vis[xxx][yyy]||xxx<1||xxx>n||yyy<1||yyy>n||bx[xxx]>=ax[xxx]||by[yyy]>=ay[yyy])continue;bx[xxx] ++;by[yyy] ++;vis[xxx][yyy]=true;path[cnt++]=g[xxx][yyy];dfs(xxx,yyy);bx[xxx] --;by[yyy] --;vis[xxx][yyy]=false;path[cnt--]=-1;		}}
int main()
{cin>>n;for(int i=1;i<=n;i++)cin>>ay[i];for(int i=1;i<=n;i++)cin>>ax[i];for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){g[i][j]=k++;}}vis[1][1]=true;path[0]=0;cout<<"0"<<" ";bx[1]=1,by[1]=1;dfs(1,1);return 0;
}