2023牛客暑期多校训练营7(C/I/M)
目录
C.Beautiful Sequence
I.We Love Strings
M.Writing Books
C.Beautiful Sequence
思路:显然若得到了a[1],则整个序列a我们都知道了。所以我们要求出第k大的a[1],这个可以利用序列a为不递减序列的性质来得出。
首先,由题意可得:
a[2]=a[1]^b[1]
a[3]=a[2]^b[2]=(a[1]^b[1])^b[2]
a[4]=a[3]^b[3]=((a[1]^b[1])^b[2])^b[3]
......
得出a[i]=a[1]^(序列b的前缀i异或和)
我们把序列b的前缀i异或和定义为f[i],因为序列a不递减,所以:
a[i]<=a[i+1]
=> a[1]^f[i-1] <= a[1]^f[i]
首先我们先初始化a[1]二进制位为-1,这代表a[1]的这个位可以是0,也可以是1。然后我们再根据a[1]^f[i-1] <= a[1]^f[i] 这个公式来得出a[1]的哪些位它是确定的,不能是-1。
我们需要从高位往低位贪心,因为如果a[1]^f[i-1]的一个高位如果是1,而a[1]^f[i]的这个位是0,那么低位再怎么变,a[1]^f[i-1]也必然小于a[1]^f[i]。比如两个二进制数1????和0????,就算左边的低位全是1,右边的高位全是0,也就是变成10000和01111,左边依然大于右边。
然后我们从高位到低位怎么贪心呢?找f[i]的f[i-1]的从高位到低位,第一个不同的位即可,我们设这个是第k位。此时a[1]的第k位必须和f[i]第k位的值相同,这样子就能让f[i]^a[1]的第k位是0,f[i+1]^a[1]第k位是1,保证了前者小于后者。在此之前a[i]的第k位必须等于-1或者等于f[i]的第k位,否则输出-1。
此时我们得到了n个-1的值,我们我们最多能表示第2的n次方大的值,此时我们只需将(k-1)拆分成二进制依次填入-1的位置即可。具体实现见代码。
代码:
void solve() {a[1]=0;mem(now,-1);int n,k;cin>>n>>k;for(int i=1; i<n; i++) {cin>>b[i];f[i]=(f[i-1]^b[i]);}for(int i=0; i<n-1; i++) {for(int j=29; j>=0; j--) {if((f[i]>>j&1ll)!=(f[i+1]>>j&1ll)) {//找到高位第一个不相等的二进制位if(now[j]==-1)now[j]=(f[i]>>j&1ll);else if(now[j]==(f[i+1]>>j&1ll)) {//如果该位已经确定,并且与想要填的数相反,则输出-1cout<<-1<<endl;return;}break;//高位比上一个大了之后,就不用再管低位了}}}k--;//去掉初始不变的情况,方便替换-1int maxx=0;for(int i=0; i<30; i++) {if(now[i]==-1)maxx=maxx*2+1;}if(maxx<k) {cout<<-1<<endl;return;}vector<int>v;while(k) {//将k转换为二进制填入v.push_back({k%2});k/=2;}reverse(v.begin(),v.end());for(int i=0; i<30; i++) {if(!v.size())break;//填完了就退出if(now[i]==-1) {//依次填入now[i]=v.back(),v.pop_back();}}for(int i=0; i<30; i++)now[i]=max(now[i],0ll);//把没填的-1变成0for(int i=29; i>=0; i--) a[1]=a[1]*2+now[i];;//得出a[1]的值cout<<a[1]<<" ";for(int i=2; i<=n; i++)cout<<(b[i-1]^a[i-1])<<" ",a[i]=(b[i-1]^a[i-1]);//根据a[1]得出整个序列acout<<endl;
}I.We Love Strings
思路:因为字符串长度不相同的字符串,两两之间肯定不能匹配,所以我们根据字符串长度大小来求解。在lenth<=20时我们暴力枚举字符串所有情况进行求解,而在lenth>20的时候我们暴力容斥来求解。
那么为什么这个临界值为20呢?
我们设临界值为N,暴力枚举所有情况的复杂度主要由字符串长度决定,复杂度为:
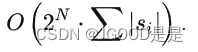
而容斥的复杂度主要由容斥的集合大小决定,而这个集合的最大大小又由n的最大值和N共同决定,它的复杂度为:

总的复杂度为他们两个相加。
此时N取太大或者取太小,都会使得一方的复杂度过大,此时取400的根号,也就是N=20,是最好的。
具体实现见代码。
代码:
int pp(vector<int>v,string s,int n) {for(int i=0; i<n; i++) {if(s[i]!='?'&&v[i]!=s[i]-'0')return 0;//如果两个串确定有位置不同了,则匹配失败 }return 1;//匹配成功
}
int f1(int n) {int sum=0;for(int i=0; i<(1<<n); i++) {//枚举这个长度01串的所有可能。 vector<int>s;for(int j=0; j<n; j++) {s.push_back((i>>j&1ll));} //将枚举的串存入vector for(int i=0; i<v[n].size(); i++) {if(pp(s,v[n][i],n)) {//如果有一个串能和这个枚举的串匹配,答案+1 sum++;break;}}}return sum;
}
int f2(int n) {int m=v[n].size(),ans=0;//注意i要从1开始,若从0开始则会使答案增加 for(int i=1; i<(1ll<<m); i++) {//枚举集合内的串int sum=1;for(int j=0; j<n; j++) {//枚举串的每个位 int cnt0=0,cnt1=0;for(int k=0; k<m; k++) {//表示这是集合内第几个串 if((i>>k&1ll)) {if(v[n][k][j]=='0')cnt0++;if(v[n][k][j]=='1')cnt1++;}}if(cnt0&&cnt1) {//若该位上确定的数不一致,则不能进行容斥 sum=0;break;}if(!cnt0&&!cnt1)sum=sum*2%mod;//该位上全是?,贡献*2 }int now=__builtin_popcount(i); if(now%2)ans=(ans+sum)%mod; //进行容斥 else ans=(ans-sum+mod)%mod;}return ans;
}
void solve() {int n,ans=0;cin>>n;for(int i=1; i<=n; i++) {string s;cin>>s;v[(int)s.size()].push_back(s);//将字符串根据长度分类 }for(int i=1; i<=400; i++) {if(!v[i].size())continue;if(i<=20)ans=(ans+f1(i))%mod;//若长度<=20则暴力求解 else ans=(ans+f2(i))%mod;//否则暴力容斥 }cout<<ans<<endl;
}M.Writing Books
思路:显然1~9对于答案的贡献为1*9,10~99对于答案的贡献为2*90,100~999对于答案的贡献为3*900......。分块求出贡献即可。
代码:
void solve() {int n,l=1,r=10,now=1,ans=0;cin>>n;while(l<=n){if(n>=r-1)ans+=(r-l)*now;else ans+=(n-l+1)*now;now++,l=r,r*=10;}cout<<ans<<endl;
}