三大基础排序算法——冒泡排序、选择排序、插入排序
目录
- 前言
- 一、排序简介
- 二、冒泡排序
- 三、选择排序
- 四、插入排序
- 五、对比
- References
前言
在此之前,我们已经介绍了十大排序算法中的:归并排序、快速排序、堆排序(还不知道的小伙伴们可以参考我的 「数据结构与算法」 专栏),今天我们就来介绍三大基础的排序算法:冒泡排序,选择排序和插入排序。
一、排序简介
排序算法(Sorting Algorithm)是一种将一组特定的数据按某种顺序进行排列的算法。排序算法多种多样,性质也大多不同。
稳定性
排序算法的稳定性并不是指最坏时间复杂度和最好时间复杂度是否相等,而是指相等的元素在经过排序之后其相对位置是否发生改变。
下图展示了稳定排序和不稳定排序之间的区别:

按照是否稳定可对十大排序算法做出如下分类:
| 稳定排序 | 不稳定排序 |
|---|---|
| 冒泡排序、插入排序、归并排序、计数排序、桶排序、基数排序 | 选择排序、希尔排序、快速排序、堆排序 |
时间复杂度
排序算法的时间复杂度分为最好时间复杂度、平均时间复杂度和最坏时间复杂度。
基于比较的排序算法的时间复杂度下限是 O(nlogn)O(n\log n)O(nlogn)。
二、冒泡排序
冒泡排序多次遍历数组,它比较相邻的元素,将不合顺序的进行交换,每一轮遍历都将下一个最大值放到正确的位置上。本质上,每个元素通过「冒泡」找到自己所属的位置。
经过 iii 次遍历后,数组末尾的 iii 项必然是最大的那 iii 项,因此冒泡排序最多需要遍历 n−1n-1n−1 遍数组就能完成排序。
动画演示:

冒泡排序实现:
// a是待排序数组,n是数组长度
void bubble_sort(int a[], int n) {for (int i = n - 1; i; i--)for (int j = 0; j < i; j++)if (a[j] > a[j + 1]) swap(a[j], a[j + 1]);
}
可以看出,若两个元素相等,则它们之间不会发生交换,因此冒泡排序具有稳定性。
冒泡排序通常被认为是效率最低的排序算法,因为在确定最终的位置前必须交换元素。注意到如果在一轮遍历中没有发生元素交换,就说明数组已经有序,此时可以提前终止以避免后续的无用功。
改进后的冒泡排序如下(又称短冒泡):
void bubble_sort(int a[], int n) {int round = n - 1; // 因为冒泡排序至多n-1轮遍历就会结束bool flag = true; // flag为false时代表一轮遍历中没有发生元素交换while (round && flag) {flag = false;for (int i = 0; i < round; i++)if (a[i] > a[i + 1]) {flag = true;swap(a[i], a[i + 1]);}round--;}
}
分析时间复杂度。若数组已经是有序的,则冒泡排序只需遍历一遍数组,不用执行任何交换操作,时间复杂度为 O(n)O(n)O(n)。显然冒泡排序的平均时间复杂度和最坏时间复杂度均为 O(n2)O(n^2)O(n2),且在最坏情况下,冒泡排序需要执行 n(n−1)/2n(n-1)/2n(n−1)/2 次交换操作。
三、选择排序
选择排序在冒泡排序的基础上进行了改进,每次遍历数组时只做一次交换。要实现这一点,选择排序在每次遍历时寻找最小值,并在遍历完后将它放到正确的位置上。第一次遍历后,最小的元素就位;第二次遍历后,第二小的元素就位,以此类推。
📝 当然也可以每次遍历时寻找最大值。
动画演示:

选择排序实现:
void selection_sort(int a[], int n) {for (int i = 0; i < n - 1; i++) {int ith = i;for (int j = i + 1; j < n; j++)if (a[j] < a[ith]) ith = j;swap(a[i], a[ith]);}
}
从代码中可以看出选择排序的最好、平均、最坏时间复杂度均为 O(n2)O(n^2)O(n2)。
选择排序是不稳定的。设有数组 [5,3,3][5,\textcolor{red}{3},\textcolor{green}{3}][5,3,3],第一轮遍历后得到 [3,3,5][\textcolor{green}{3},\textcolor{red}{3},5][3,3,5],第二轮遍历时不会有任何元素交换,可以看到两个 333 的相对位置发生了改变。
四、插入排序
插入排序是一种简单直观的排序算法。它在列表较低的一端(即索引较小的一端)维护一个有序子数组,并逐个将每个新元素「插入」这个子数组。
一个与插入排序相同的操作是打扑克牌时,从牌桌上抓一张牌,按牌面大小插到手牌后,再抓下一张牌。
动画演示:
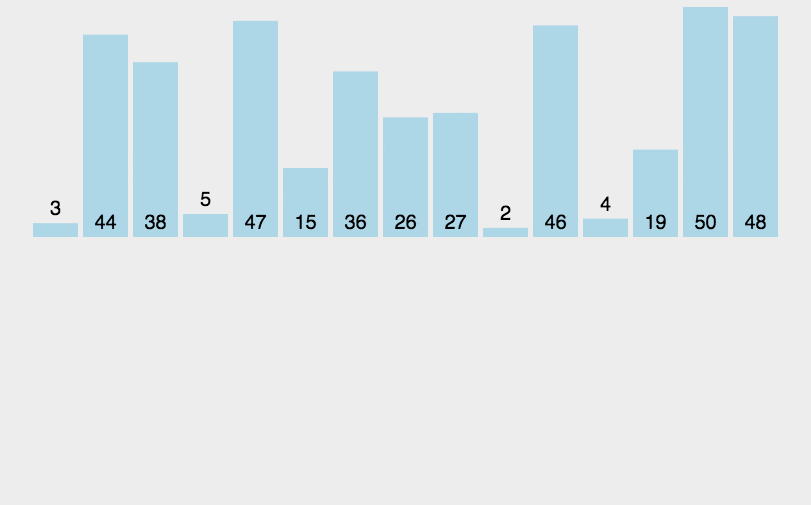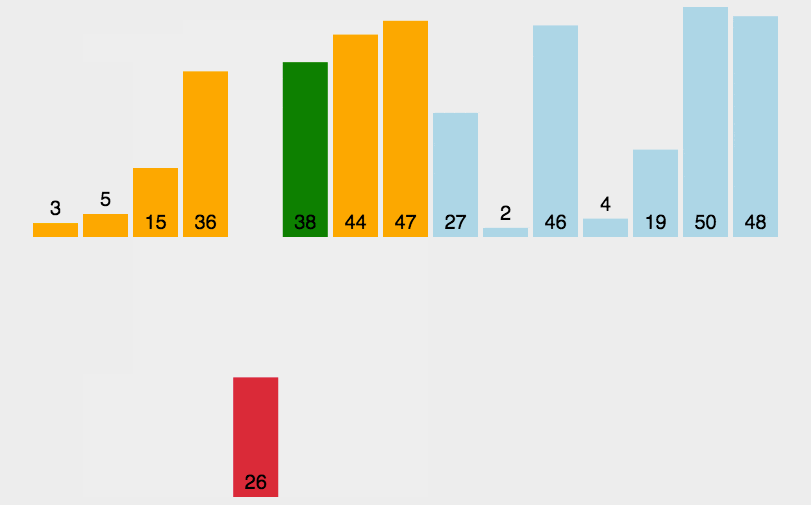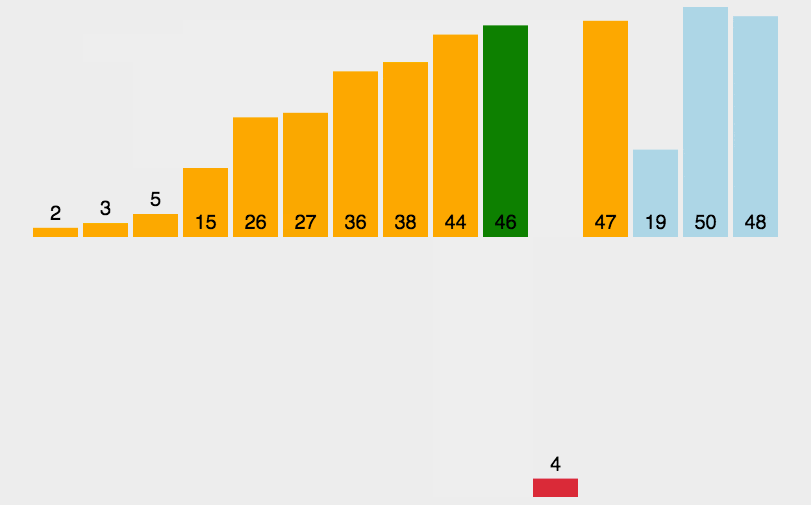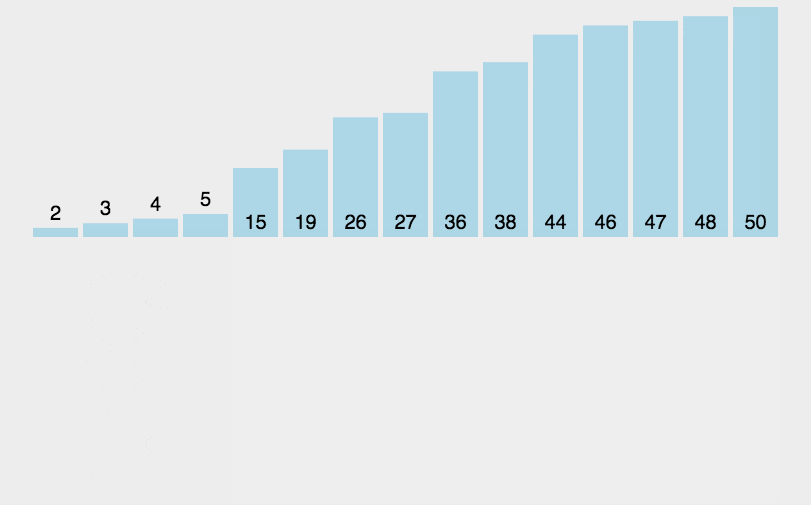
插入排序实现:
void insertion_sort(int a[], int n) {for (int i = 1; i < n; i++) {int key = a[i];int j = i - 1;while (j >= 0 && a[j] > key) {a[j + 1] = a[j];j--;}a[j + 1] = key;}
}
在数组已经是有序的情况下,while 循环不会被执行,因此插入排序的最好时间复杂度为 O(n)O(n)O(n)。显然,插入排序的平均时间复杂度和最坏时间复杂度均为 O(n2)O(n^2)O(n2)。
插入排序是稳定的,因为它会将待插入元素插入到有序子数组中首个发现的大于等于该元素的位置(因为是从右向左遍历,所以首个发现的位置一定靠右),并不会发生交换。
这里再介绍一下二分插入排序。因为数组的左边已经是有序的了,所以可以用二分查找去寻找待插入元素应当插入的位置。<algorithm> 库中有一个 upper_bound 函数,它可以用来查找一个有序序列中首个大于 xxx 的元素,并返回指向该元素的迭代器。
二分插入排序的实现:
void insertion_sort(int a[], int n) {for (int i = 1; i < n; i++) {int key = a[i];int mid = upper_bound(a, a + i, key) - a;for (int j = i - 1; j >= mid; j--) a[j + 1] = a[j];a[mid] = key;}
}
从时间复杂度的角度来看,二分插入排序与直接插入排序相同。
五、对比
三大基础排序算法的比较列在下表中:
| 排序算法 | 最好时间复杂度 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n)O(n)O(n) | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 稳定 |
| 选择排序 | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 不稳定 |
| 插入排序 | O(n)O(n)O(n) | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 稳定 |
References
[1] https://oi-wiki.org/basic/sort-intro/
[2] https://zh.wikipedia.org/wiki/%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95
[3] https://www.runoob.com/w3cnote/ten-sorting-algorithm.html
[4] https://zhuanlan.zhihu.com/p/42586566
