【LeetCode】647. 回文子串
题目链接
文章目录
- 1. 思路讲解
- 1.1 方法选择
- 1.2 dp表的创建
- 1.3 状态转移方程
- 1.4 填表顺序
- 2. 代码实现
1. 思路讲解
1.1 方法选择
这道题我们采用动态规划的解法,倒不是动态规划的解法对于这道题有多好,它并不是最优解。但是,这道题的动态规划思想是非常有用的,我们使用这道题的动态规划思想,可以让一些hard题变为easy题。
也就是说,这道题的动态规划思想其实就是起到了一个抛砖引玉的作用。
1.2 dp表的创建
如何表示出所有的子串的情况?可以用 i 表示某个子串的起始位置,用 j 来表示某个子串的末尾位置,暴力枚举,可以在N^2的时间复杂度内求出所有子串是否为回文子串。
所以,我们用二维dp[i][j]表来表示,以 i 位置为起始位置且以 j 位置为结尾的子串是否为回文子串。如果为回文子串那么dp[i][j]为true,否则为false。(我们人为规定 i <= j)
1.3 状态转移方程
我们要知道dp[i][j]为是否为回文子串,首先要判断 s[i] 是否等于 s[j]。
如果 s[i] != s[j],那么不管 i 和 j 中间的元素序列是怎样的,以 i 位置为起始位置,以 j 位置为终止位置的子串一定不为回文子串。
如果 s[i] == s[j],那么需要对 i 和 j 的位置进行判断。
- 如果 i == j,那么说明当前初识位置和末尾位置在同一个位置,也就是说,子串只有一个元素,此时根据题意它为回文子串;
- 如果 i + 1 == j,那么 i 和 j 的位置是相邻的,此时它们中间没有元素,它们位置上的元素又相同,那么一定是回文子串;
- 如果 i + 1 < j,说明 i 位置 和 j 位置中间还有其他元素,此时只需判断dp[i+1][j-1]为true还是false即可。
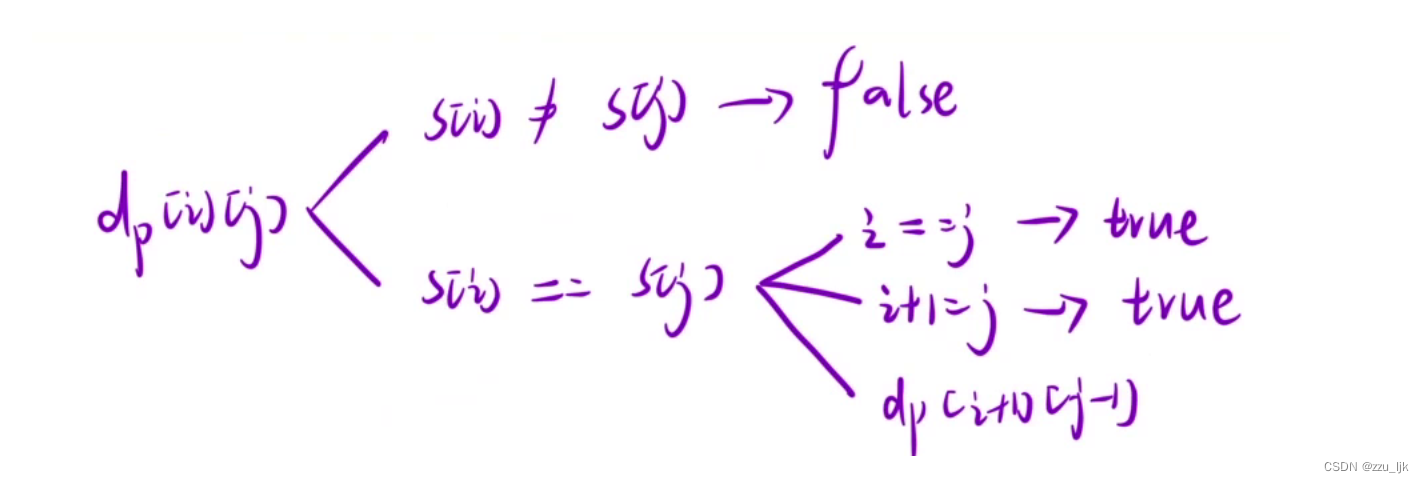
1.4 填表顺序
由于我们求dp[i][j]的时候,需要用到 dp[i+1][j-1],且 i 的循环为外层的循环,所以让 i 从大到小循环即可。
2. 代码实现
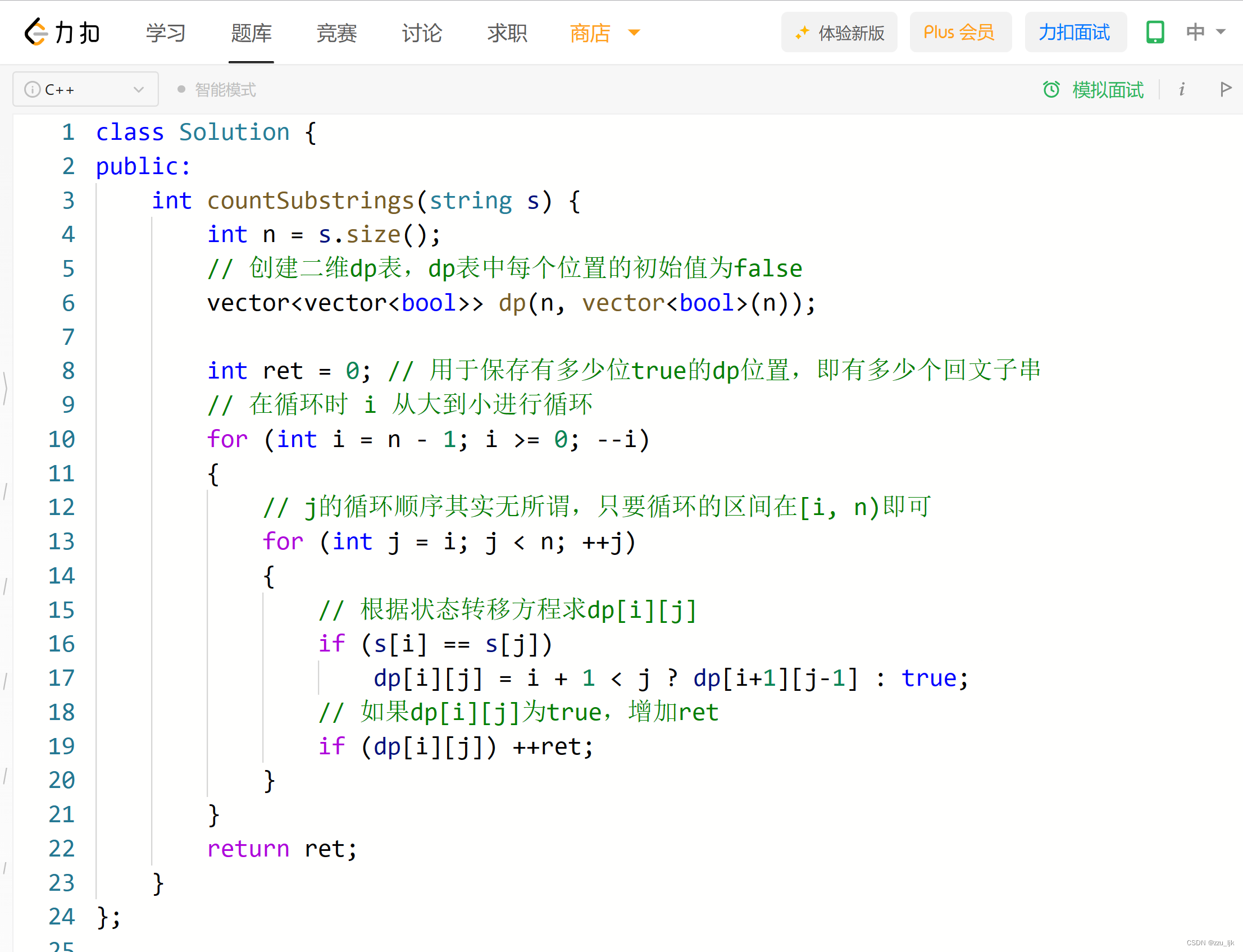
class Solution {
public:int countSubstrings(string s) {int n = s.size();// 创建二维dp表,dp表中每个位置的初始值为falsevector<vector<bool>> dp(n, vector<bool>(n));int ret = 0; // 用于保存有多少位true的dp位置,即有多少个回文子串// 在循环时 i 从大到小进行循环for (int i = n - 1; i >= 0; --i){// j的循环顺序其实无所谓,只要循环的区间在[i, n)即可for (int j = i; j < n; ++j){// 根据状态转移方程求dp[i][j]if (s[i] == s[j])dp[i][j] = i + 1 < j ? dp[i+1][j-1] : true;// 如果dp[i][j]为true,增加retif (dp[i][j]) ++ret;}}return ret;}
};
