当前位置：首页 > news >正文

第三章图论 No.4最小生成树的简单应用

news 2025/7/24 3:59:59

文章目录

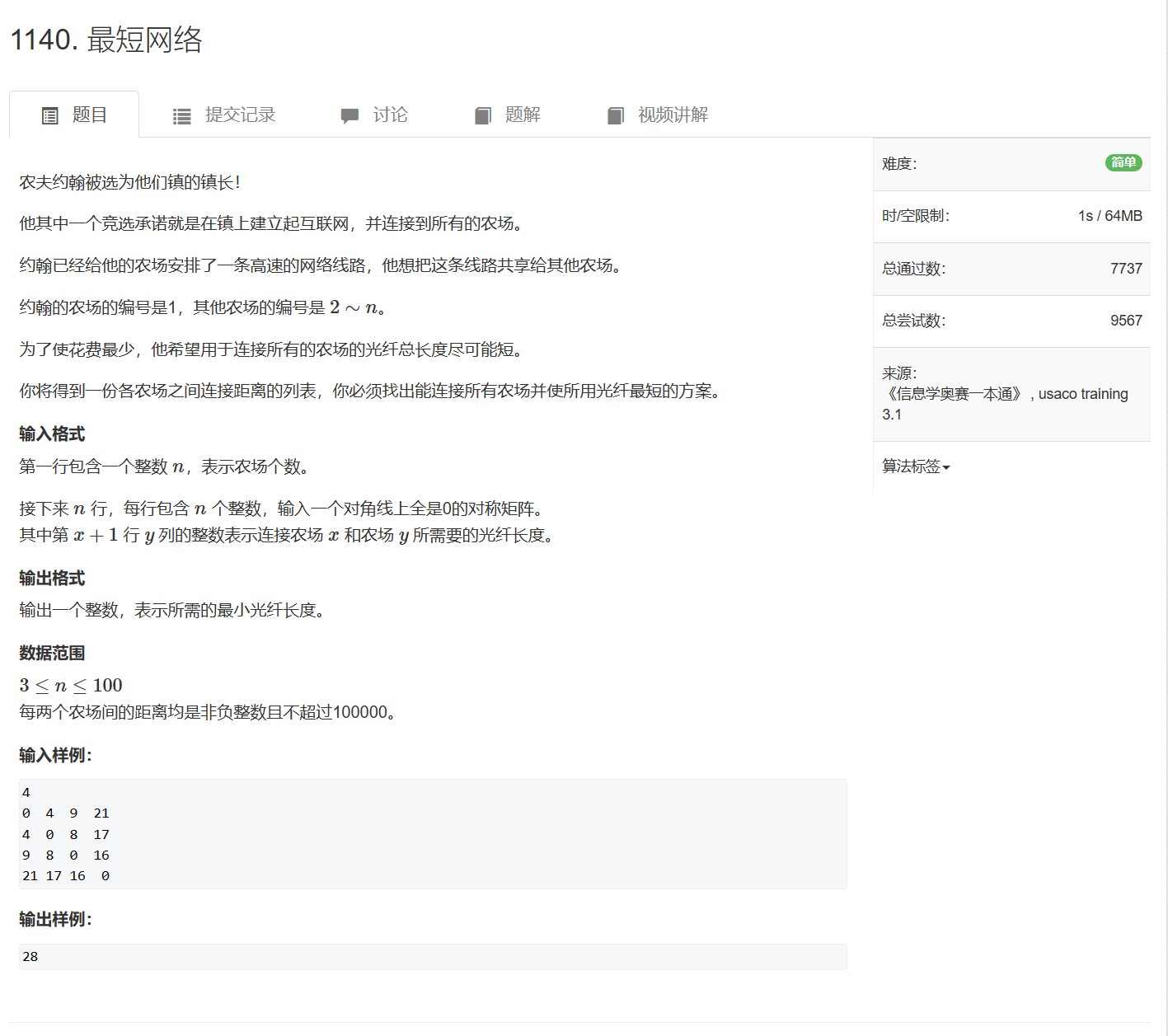
- - 裸题：1140. 最短网络
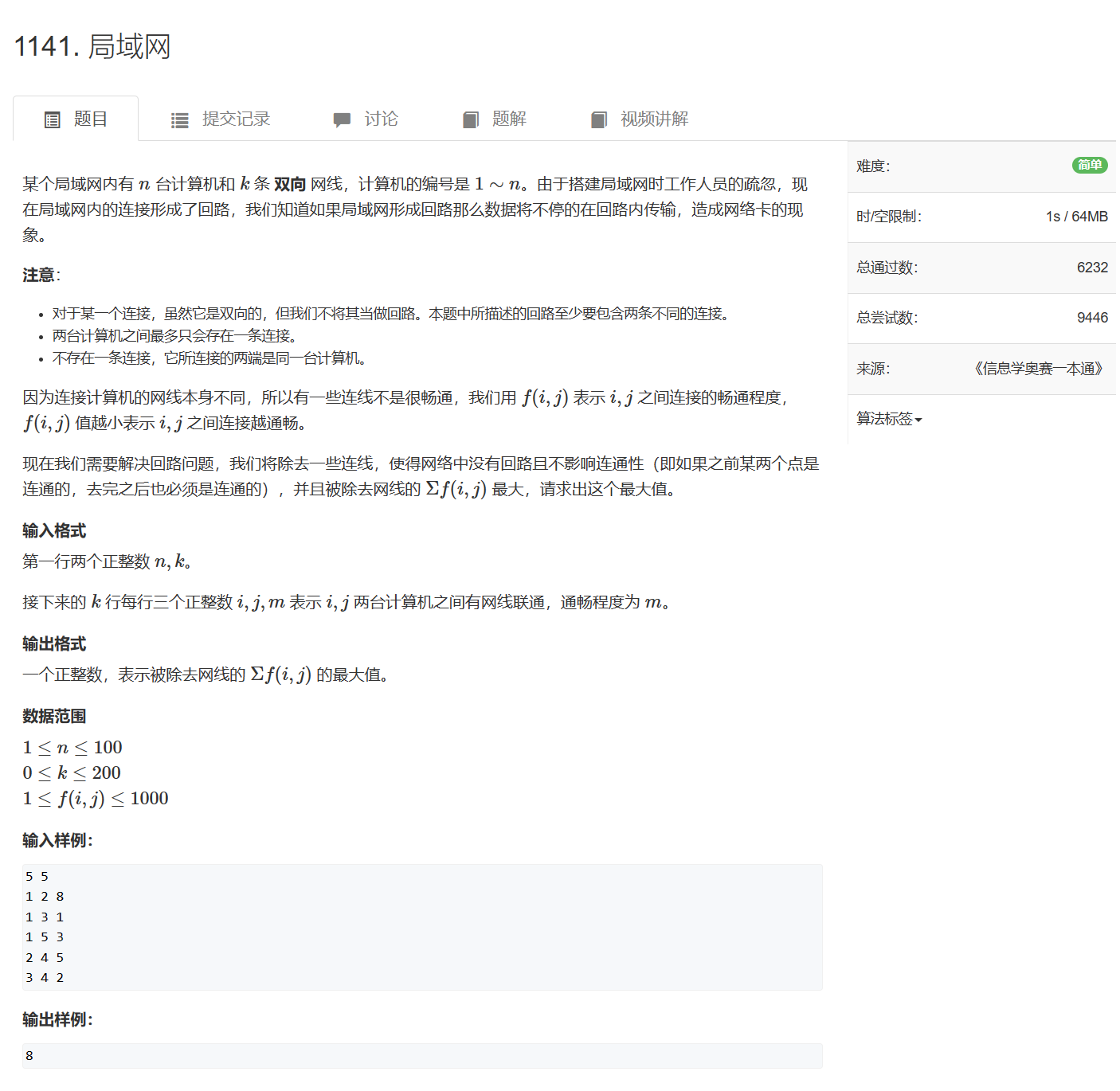
  - 裸题：1141. 局域网
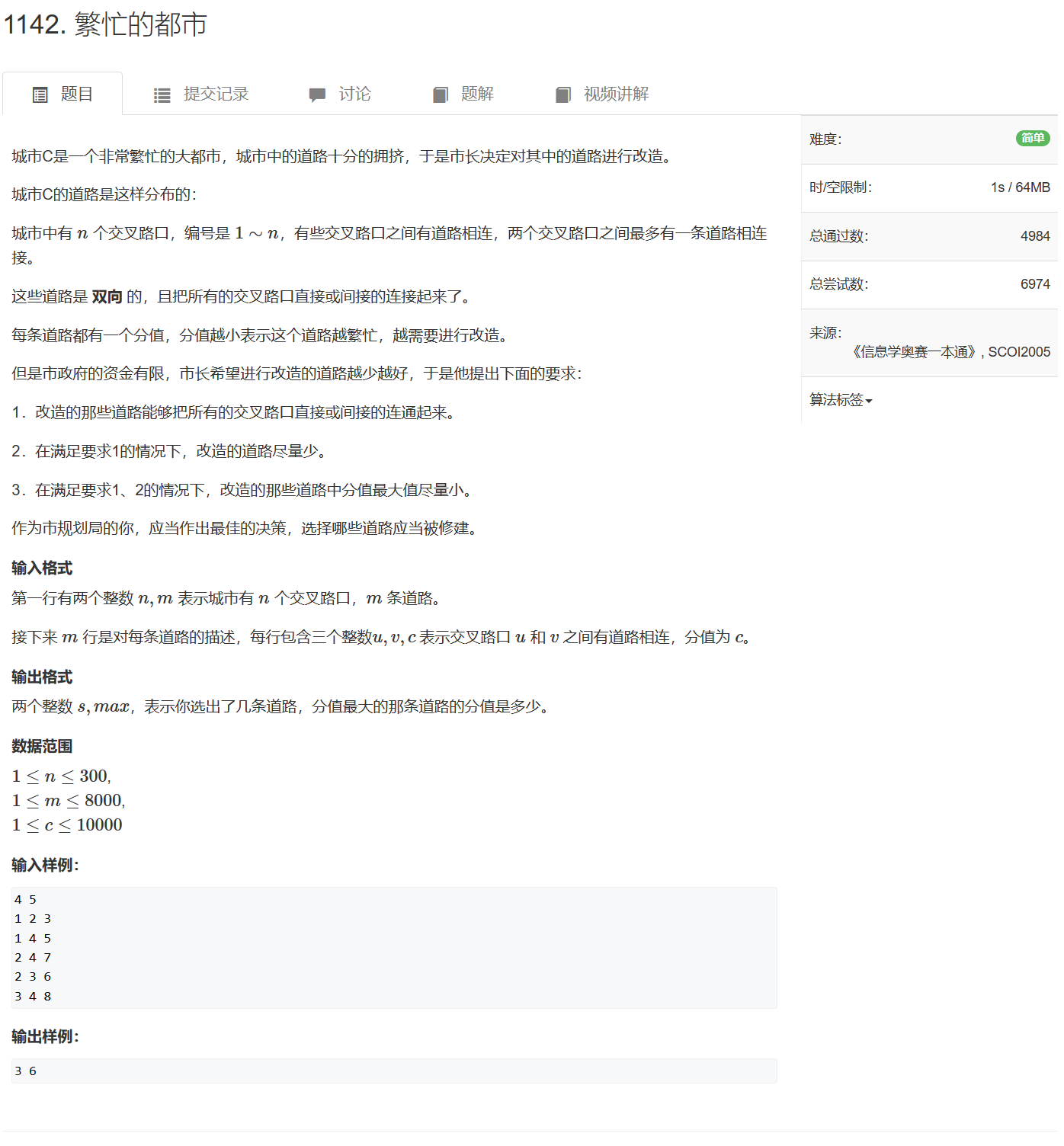
  - 裸题：1142. 繁忙的都市
  - 裸题：1143. 联络员
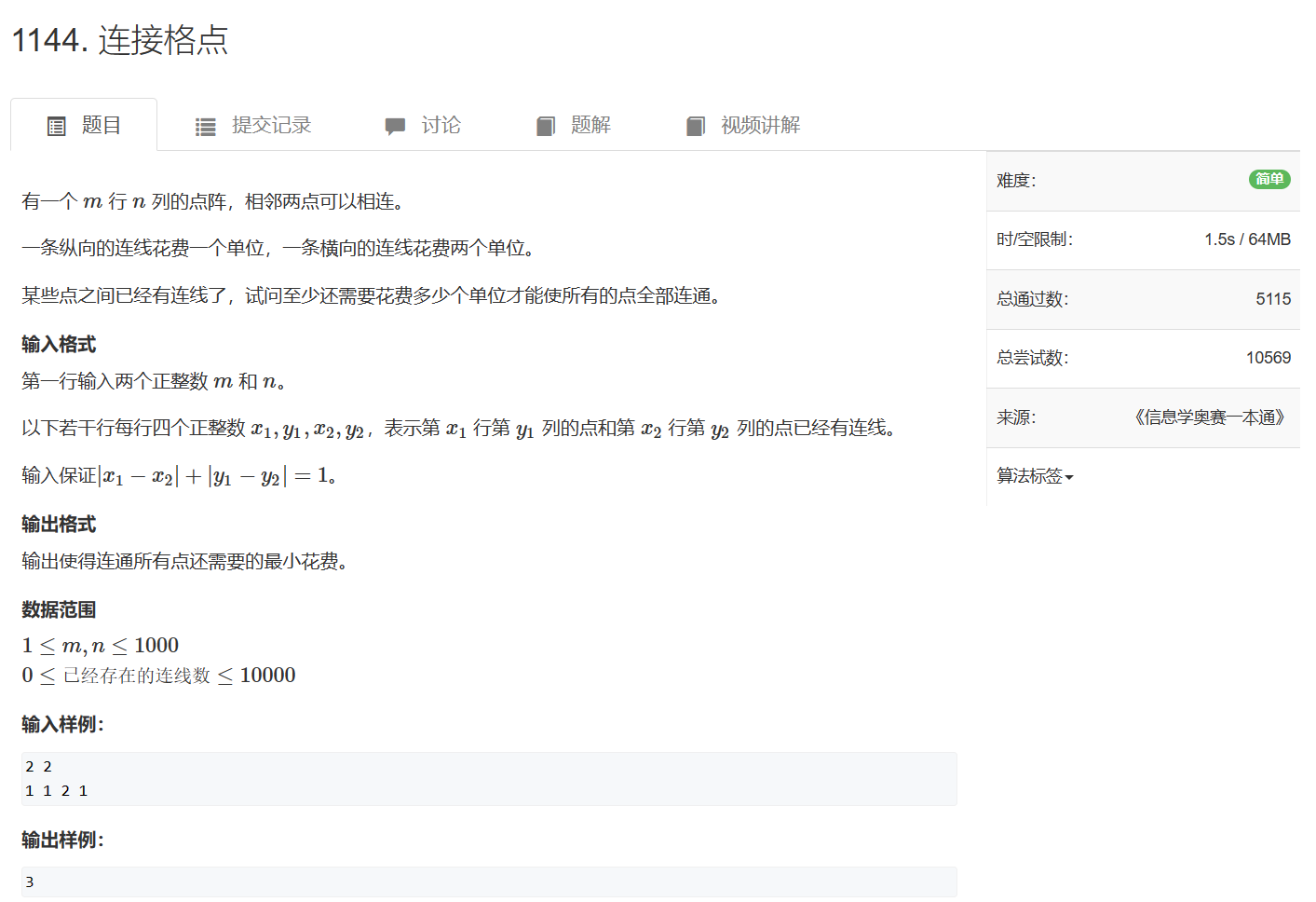
  - 有些麻烦的裸题：1144. 连接格点

存在边权为负的情况下，无法求最小生成树

裸题：1140. 最短网络

1140. 最短网络 - AcWing题库

套个prim的板子即可

#include <iostream>
#include <cstring>
using namespace std;const int N = 110, INF = 0x3f3f3f3f;
int g[N][N];
int dis[N]; bool st[N];
int n;int prim()
{memset(dis, 0x3f, sizeof(dis));int res = 0;for (int i = 0; i < n; ++ i ){int x = -1;for (int j = 1; j <= n; ++ j ) if (!st[j] && (x == -1 || dis[x] > dis[j])) x = j;st[x] = true;if (i && dis[x] == INF) return INF;if (i) res += dis[x];for (int y = 1; y <= n; ++ y )dis[y] = min(dis[y], g[x][y]);}return res;
}int main()
{scanf("%d", &n);for (int i = 1; i <= n; ++ i )for (int j = 1; j <= n; ++ j )scanf("%d", &g[i][j]);printf("%d\n", prim());return 0;
}

裸题：1141. 局域网

1141. 局域网 - AcWing题库

裸题，稀疏图，套个kruskal的板子就行
需要注意的是：题目给定的图可能存在多个连通块，若使用prim算法，需要对每个连通块求最小生成树，但是使用kruskal能直接求出所有连通块的最小生成树

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;const int N = 110, M = 210;
struct Edge
{int x, y, w;bool operator<(const Edge& e) const {return w < e.w;}
}edges[M];int p[N];
int n, m;int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}int kruskal()
{sort(edges, edges + m);for (int i = 1; i <= n; ++ i ) p[i] = i;int cnt = 0, res = 0;for (int i = 0; i < m; ++ i ){auto t = edges[i];int x = edges[i].x, y = edges[i].y, w = edges[i].w;x = find(x), y = find(y);if (x != y){cnt ++ ;res += w;p[x] = y;}}return res;
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < m; ++ i )scanf("%d%d%d", &edges[i].x, &edges[i].y, &edges[i].w);int sum = 0;for (int i = 0; i < m; ++ i ) sum += edges[i].w;printf("%d\n", sum - kruskal());return 0;
}

裸题：1142. 繁忙的都市

1142. 繁忙的都市 - AcWing题库
依然是套kruskal的板子

#include <iostream>
#include <algorithm>
using namespace std;const int N = 310 ,M = 8010;
struct Edge
{int x, y, w;bool operator<(const Edge& e) const{return w < e.w;}
}edges[M];int n, m;
int p[N];int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}int kruskal()
{sort(edges, edges + m);int res = 0;for (int i = 1; i <= n; ++ i ) p[i] = i;for (int i = 0; i < m; ++ i ){auto t = edges[i];int x = t.x, y = t.y, w = t.w;x = find(x), y = find(y);if (x != y){res = max(res, w);p[x] = y;}}return res;
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < m; ++ i )scanf("%d%d%d", &edges[i].x, &edges[i].y, &edges[i].w);printf("%d %d\n", n - 1, kruskal());return 0;
}

裸题：1143. 联络员

1143. 联络员 - AcWing题库

添加所有必选的边，维护并查集，然后再对非必选的边做kruskal


#include <iostream>
#include <algorithm>
using namespace std;const int N = 2010, M = 10010;
struct Edge
{int x, y, w;bool operator<(const Edge& e) const {return w < e.w;}
}edges[M];int n, m, cnt;
int p[N];int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}int kruskal()
{int res = 0;for (int i = 0; i < cnt; ++ i ){auto t = edges[i];int x = t.x, y = t.y, w = t.w;x = find(x), y = find(y);if (x != y){res += w;p[x] = y;}}return res;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++ i ) p[i] = i;int t, x, y, d;int res = 0;while ( m -- ){scanf("%d%d%d%d", &t, &x, &y, &d);if (t == 1){x = find(x), y = find(y);if (x != y) p[x] = y;res += d;}else{edges[cnt].x = x, edges[cnt].y = y, edges[cnt].w = d;cnt ++ ;}}sort(edges, edges + cnt);res += kruskal();printf("%d\n", res);return 0;
}

有些麻烦的裸题：1144. 连接格点

1144. 连接格点 - AcWing题库

点阵为图中的点，将二维坐标转换成一维，作为点的编号
添加已有连线后，做kruskal即可

#include <iostream>
#include <algorithm>
using namespace std;const int N = 1010;
struct Edge
{int x, y, w;bool operator<(const Edge& e) const {return w < e.w;}
}edges[2 * N * N];int n, m, cnt = 1;
int p[N * N];
int g[N][N]; // 二维到一维
int dx[3] = { 0, 1, 0 }, dy[3] = { 0, 0, 1 };int find(int x)
{if (x != p[x]) p[x] = find(p[x]);return p[x];
}int kruskal()
{int res = 0;for (int i = 0; i < cnt; ++ i ){auto t = edges[i];int x = t.x, y = t.y, w = t.w;x = find(x), y = find(y);if (x != y){res += w;p[x] = y;}}return res;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++ i )for (int j = 1; j <= m; ++ j )g[i][j] = cnt ++ ;for (int i = 1; i < cnt; ++ i ) p[i] = i;int x1, x2, y1, y2;while (~scanf("%d%d%d%d", &x1, &y1, &x2, &y2)){int x = g[x1][y1], y = g[x2][y2];x = find(x), y = find(y);if (x != y) p[x] = y;}cnt = 0;for (int i = 1; i <= n; ++ i )for (int j = 1; j <= m; ++ j )for (int k = 1; k <= 2; ++ k ){int a = i + dx[k], b = j + dy[k];if (a >= 1 && a <= n && b >= 1 && b <= m){int x = g[i][j], y = g[a][b];edges[cnt ++ ] = { x, y, k };}}sort(edges, edges + cnt);printf("%d\n", kruskal());return 0;
}