34.利用matlab解 多变量多目标规划问题(matlab程序)
1.简述
学习目标:适合解 多变量多目标规划问题,例如 收益最大,风险最小
主要目标法,线性加权法,权值我们可以自己设定。
收益函数是 70*x(1)+66*x(2) ;
风险函数是 0.02*x(1)^2+0.01*x(2)^2+0.04*(x(1)+x(2))^2
用收益函数乘以权值0.5减去风险函数乘以0.5,然后取负, 则转变为求单一目标的最小值问题,
ff1是收益函数,ff2是风险函数
2.代码
function example_4_b()
clc
clear
f=@(x)-0.5*(70*x(1)+66*x(2))+0.5*(0.02*x(1)^2+0.01*x(2)^2+0.04*(x(1)+x(2))^2);
%fun='[-(70*x(1)+66*x(2)),0.02*x(1)^2+0.01*x(2)^2+0.04*(x(1)+x(2))^2]';
x0=[1000,1000];
A=[1 1];
B=5000;
Aeq=[]; Beq=[];
lb=[0 0];ub=[inf inf];
options=optimset('display','iter','Tolx',1e-8);
[x_f,fval_f, exitflag]=fmincon(f,x0,A,B,Aeq,Beq,lb,ub,[],options)
ff1=70*x_f(1)+66*x_f(2) %收益函数
ff2=0.02*x_f(1)^2+0.01*x_f(2)^2+0.04*(x_f(1)+x_f(2))^2 %风险函数
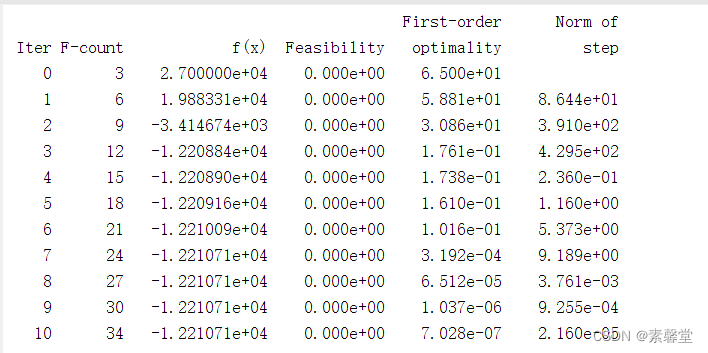
3.运行结果