I- yh的线段(2023河南萌新联赛第(四)场:河南大学)
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
yh喜欢好线段,好线段即两条线段相交且不与其他线段重合的线段。
两条线段[l1,r1]和[l2,r2]相交(如果存在至少一个x,使得l1≤x≤r1和l2≤x≤r2,则认为两个线段相交)。
yh在数轴上有几条线段,他可以把在数轴上相交的线段结合,但是对于每个线段只能与其它线段结合一次,且不能与其它线段有重合部分,yh可以舍弃任何数量的线段。
给你nn (2≤n≤1e6)条线段,如果两条线段相交且不与其他线段相交,则由这两条线段组成的线段被称为好线段,线段不能被重复使用,但可以被舍弃任意数量的线段,请你找出好线段个数的最大值。
输入描述:
第一行包含一个正数nn (2≤n≤1e6)——线段的个数。 接下来 nn行各包含两个整数li 和 ri (0≤li≤ri≤10^9,表示n 个线段。
输出描述:
输出好线段个数的最大值。
示例1
输入
复制
5 2 2 2 8 0 10 1 2 5 6
输出
复制
1
示例2
输入
复制
7 2 4 9 12 2 4 7 7 4 8 10 13 6 8
输出
复制
3
说明
对于样例2,我们可以删除[4,8]这一条线段,然后将[2,4]和[2,4]、[6,8]和[7,7]、[9,12]和[10,13]组成三条好线段,可以看出这是最优的情况。
思路:
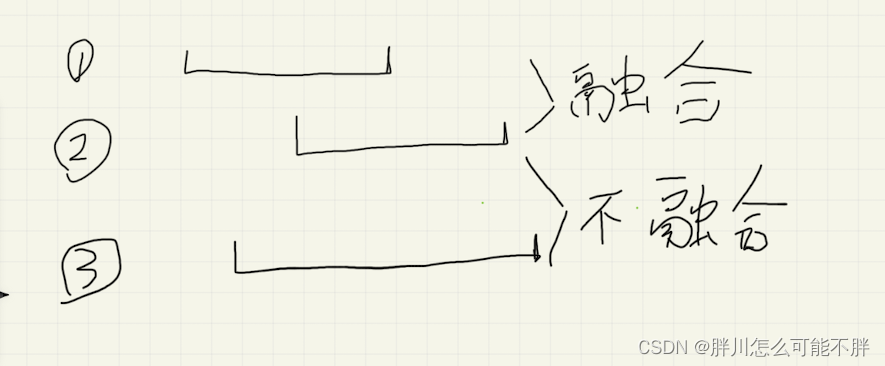
将所有线段,按照右端点从小到大进行排序。找到俩俩包含的,如果后面出现想包裹住前面的直接跳过;

当出现俩俩融合一线段之后,又出现一条直线想包含其中一条直线,那直接跳过
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<string>
#include<algorithm>
#include<unordered_map>
#include<map>
#include<bitset>
#include<cstring>
#include <unordered_set>
//#include<priority_queue>
#include<queue>
#include<deque>
#include<set>
#include<stdlib.h>
#define dbug cout<<"hear!"<<endl;
#define rep(a,b,c) for(ll a=b;a<=c;a++)
#define per(a,b,c) for(ll a=b;a>=c;a--)
#define no cout<<"NO"<<endl;
#define yes cout<<"YES"<<endl;
#define endl "\n"
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//priority_queue<int,vector<int>,greater<int> >q;
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> PII;
typedef pair<long double,long double> PDD;ll INF = 0x3f3f3f3f;
//const ll LINF=LLONG_MAX;
// int get_len(int x1,int y1,int x2,int y2)
// {
// return (x2-x1)*(x2-x1) + (y2-y1)*(y2-y1);
// }
const ll N = 1e6+ 10;
const ll mod1 =998244353;
const ll mod2 =1e9+7;
const ll hash_num = 3e9+9;
ll n,m,ca, k,ans;
ll arr[N],brr[N],crr[N];
//ll h[N],ne[N],e[N],w[N],book[N],idx;struct node
{ll l, r;
}noda[N];bool cmp(node a,node b)
{if(a.r==b.r){return a.l>b.l;}return a.r<b.r;
}void solve()
{cin >> n;rep(i,1,n){cin >> noda[i].l >> noda[i].r;}sort(noda+1,noda+1+n,cmp);ll ans=0;ll f=-1,r=-1;// cout << endl;// rep(i,1,n)// {// cout << noda[i].l <<" "<<noda[i].r<<endl;// }// cout << endl;rep(i,1,n){if(noda[i].l<=f)continue;else if(noda[i].l<=r){ans++;f=noda[i].r;}else{r=noda[i].r;}// cout << f << " "<<r<<endl;}cout << ans;
}int main()
{IOS;ll _;_=1;//get_eulers();//scanf("%lld",&_);//cin>>_;ca=1;while(_--){solve(); ca++;} return 0;
}