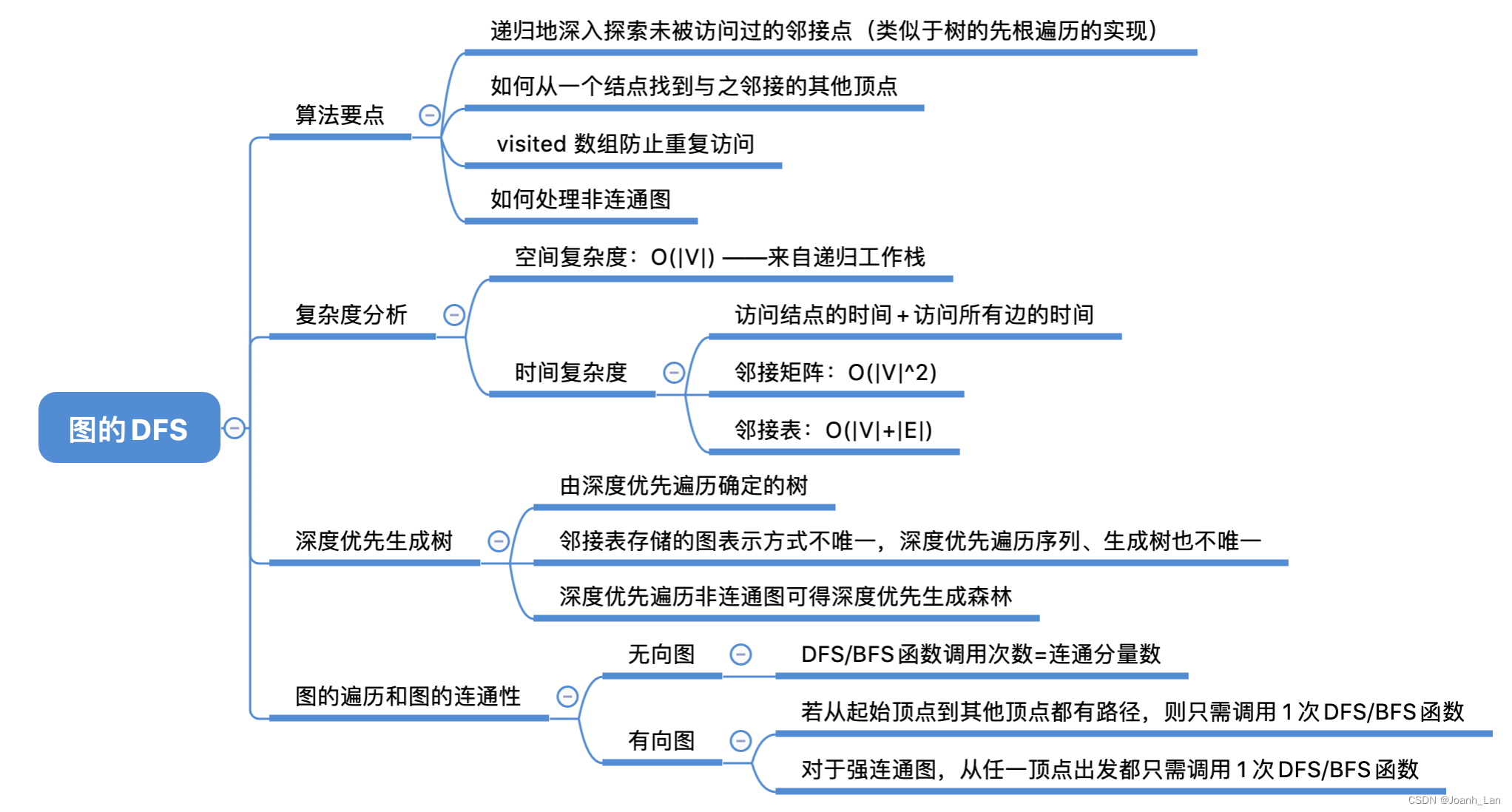
数据结构--图的遍历 DFS
数据结构–图的遍历 DFS
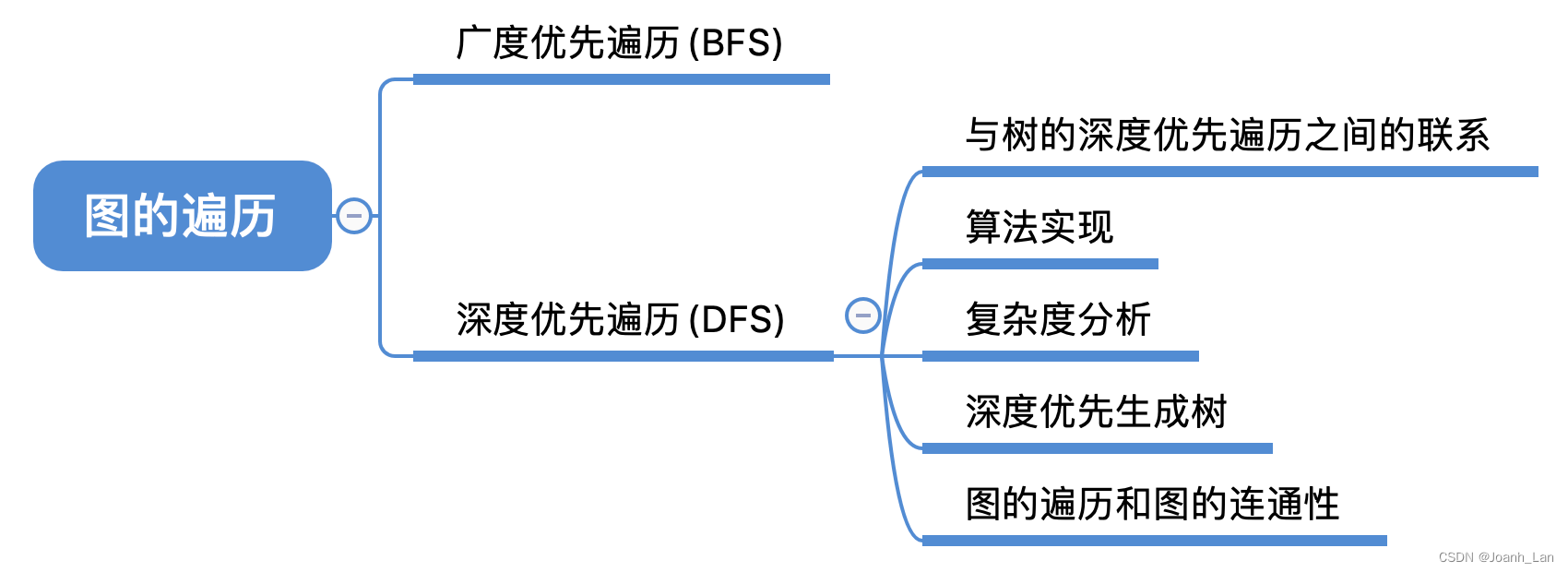
树的深度优先遍历

//树的先根遍历
void PreOrder(TreeNode *R)
{if(R != NULL){visit(R); //访问根节点while(R还有下一个子树T)PreOrder(T);//先根遍历下一棵子树}
}
图的深度优先遍历


bool visited [MAX_VERTEX_NUM]; //访问标记数组
void DFS(Graph G, int v) //从顶点v出发,深度优先遍历图
{visit(v);//访问顶点visited[v] = TRUE; //设已访问标记{for(w = FirstNeighbor(G, v); w >= 0; w = NextNeighor(G, v, w))if(!visited[w]) //w为u的尚未访问的邻接顶点DFS(G, w);}
}
如果是⾮连通图,则⽆法遍历完所有结点
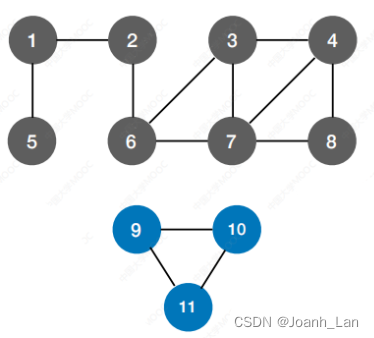
bool visited[MAX_VERTEX_NUM]; //访问标记数组void DFSTraverse(Graph G)//对图G进行深度优先遍历
{for(v = 0; v < G.vexnum; ++v)visited[v] = FALSE;//初始化已访问标记数据for(v = 0; v < G.vexnum; ++v)if(!visited[v])DFS(G, v);//本代码中是从v=0开始遍历
}void DFS(Graph G, int v) //从顶点v出发,深度优先遍历图G
{visit(v);//访问顶点vvisited[v] = TRUE; //设已访问标记for(w = FirstNeighbor(G, v); w >= 0; w = NextNeighor(G, v, w))if(!visited[w]) //w为u的尚未访问的邻接顶点DFS(G,w);
}
复杂度分析

空间复杂度:来⾃函数调⽤栈,最坏情况,递归深度为 O ( ∣ V ∣ ) \color{red}空间复杂度:来⾃函数调⽤栈,最坏情况,递归深度为O(|V|) 空间复杂度:来⾃函数调⽤栈,最坏情况,递归深度为O(∣V∣)

空间复杂度:最好情况, O ( 1 ) \color{purple}空间复杂度:最好情况,O(1) 空间复杂度:最好情况,O(1)
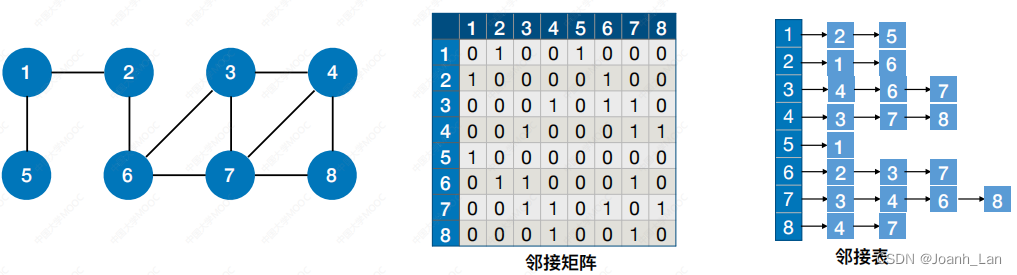
时间复杂度=访问各结点所需时间+探索各条边所需时间
邻接矩阵 \color{red}邻接矩阵 邻接矩阵存储的图:
访问 |V| 个顶点需要O(|V|)的时间
查找每个顶点的邻接点都需要O(|V|)的时间,⽽总共有|V|个顶点
时间复杂度= O ( ∣ V ∣ 2 ) \color{red}O(|V|^2) O(∣V∣2)
邻接表 \color{red}邻接表 邻接表存储的图:
访问 |V| 个顶点需要O(|V|)的时间
查找各个顶点的邻接点共需要O(|E|)的时间,
时间复杂度= O ( ∣ V ∣ + ∣ E ∣ ) \color{red}O(|V|+|E|) O(∣V∣+∣E∣)
注:
同⼀个图的 邻接矩阵 \color{red}邻接矩阵 邻接矩阵表示⽅式 唯⼀ \color{red}唯⼀ 唯⼀,因此 深度优先遍历序列唯⼀ \color{red}深度优先遍历序列唯⼀ 深度优先遍历序列唯⼀
同⼀个图 邻接表 \color{red}邻接表 邻接表表示⽅式 不唯⼀ \color{red}不唯⼀ 不唯⼀,因此 深度优先遍历序列不唯⼀ \color{red}深度优先遍历序列不唯⼀ 深度优先遍历序列不唯⼀
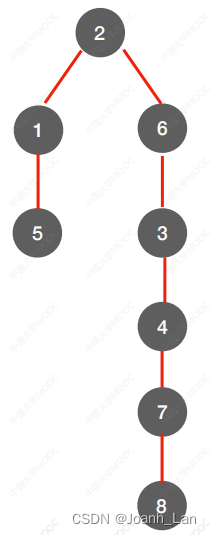
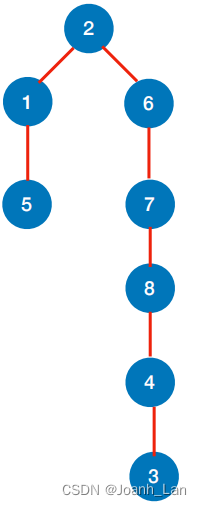
深度优先⽣成树

同⼀个图的邻接矩阵表示⽅式唯⼀,因此深度优先遍历序列唯⼀,深度优先⽣成树也唯⼀
同⼀个图邻接表表示⽅式不唯⼀,因此深度优先遍历序列不唯⼀,深度优先⽣成树也不唯⼀
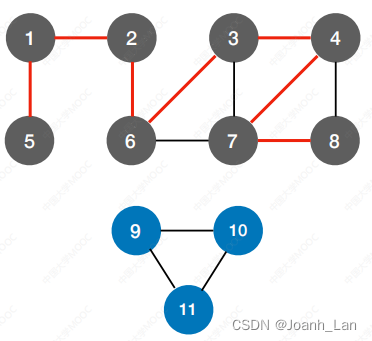
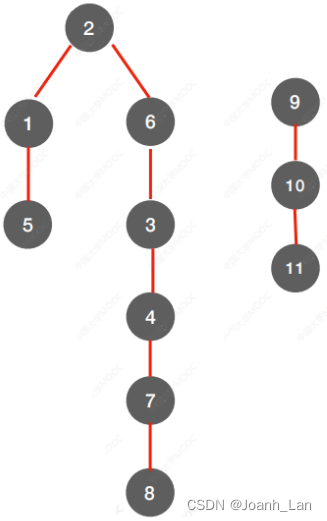
深度优先⽣成森林
图的遍历与图的连通性

对 ⽆向图 \color{red}⽆向图 ⽆向图进⾏BFS/DFS遍历
调⽤BFS/DFS函数的次数=连通分量数
对于 连通图 \color{red}连通图 连通图,只需调⽤1次 BFS/DFS
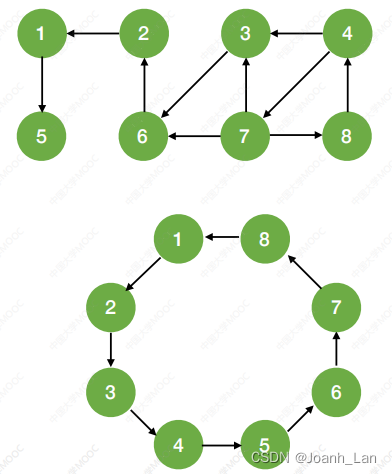
对 有向图 \color{red}有向图 有向图进⾏BFS/DFS遍历
调⽤BFS/DFS函数的次数要具体问题具体分析
若起始顶点到其他各顶点都有路径,则只需调⽤1次
BFS/DFS 函数
对于 强连通图 \color{red}强连通图 强连通图,从任⼀结点出发都只需调⽤1次 BFS/DFS
知识回顾与重要考点