LinearAlgebraMIT_6_ColumnSpaceAndNullSpace
这节课的两个重点是column space列空间和null space零空间。
x.1 pre-multiply/left multiply and post-multiply/right multiply
对于pre-multiply/left multiply左乘和post-multiply/right multiply右乘,如果用英文的pre-和post-是比较容易理解的, A B AB AB的意思是: A A A左乘(于) B B B或者 B B B右乘(于) A A A。
x.2 Linear Combination
linear combination线性组合是线性代数的核心,我们以举例子的方式来讲解线性组合,假设我们有一个4行3列的矩阵,我们将矩阵列分成3个向量构成的向量组 [ α 1 , α 2 , α 3 ] [\alpha_1, \alpha_2, \alpha_3] [α1,α2,α3],用这个向量组左乘于一个3*1的列向量,则是由列向量构成的向量组的线性组合。

同理,将矩阵A行分后便是行向量的线性组合。
x.3 Vector Space and Subspace
我们首先回忆一下上节课的内容,上节课的重点内容是vector space向量空间和subspace子空间。向量空间的定义是,对于数乘和相加都是封闭的空间,即空间中的任一向量的相加或者数乘后的结果都还在向量空间中,值得注意的一点是,向量空间中一定包含零点。向量空间还有一种定义是从线性组合的角度来阐述的,即对于向量空间中任一向量的线性组合仍然在该空间中。如R3就是向量空间。

已知向量空间后,我们再引入子空间的概念,子空间是向量空间的子集,子空间的定义是子空间中的任一向量的数乘和相加都在子空间中,且注意子空间一定有零点。例如,R3的子空间就有过零点的平面和过零点的直线组成的向量。
对于两个子空间,我们还得知道两个关于子空间的性质,我们任取两个子空间P和L,他们的并集不构成子空间,但是他们的交集构成子空间。因为两个子空间相交后,可能并不是所有向量的相加操作都在子空间中,例如一条过零点的直线(且直线不在平面上)和一个过零点的平面,他们两个的并集就不构成子空间。

x.4 Column Space and Null Space
Column Space列空间和Null Space零空间是两种特殊的子空间。为了方便理解我们引入A为3*4矩阵的例子。假设A矩阵如下,
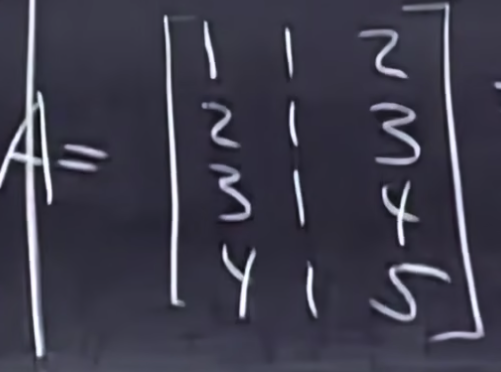
我们将A矩阵列分得到向量组 [ 1 , 2 , 3 , 4 ] , [ 1 , 1 , 1 , 1 ] , [ 2 , 3 , 4 , 5 ] [1, 2, 3, 4], [1, 1, 1, 1], [2, 3, 4, 5] [1,2,3,4],[1,1,1,1],[2,3,4,5],显而易见这是R4的向量组成的向量组,且单单这三个向量并不能构成向量空间或者子空间,我们现在想做的是,找到由这三个向量所有的线性组合组构成的向量子空间。而由前面的知识我们知道,线性组合的问题和解线性方程组的问题是一样的,我们将上面的意思翻译一下,也可以理解成是解一个Ax=b的非齐次线性方程组,而我们要做的是找到一个向量子空间,这个子空间包含所有的向量[b1, b2, b3, b4]。[x1, x2, x3]是线性组合的系数,这里我们只关注系数b,所有的系数b便构成了列空间。
首先我们需要注意,Ax=b并不一定一直有解,因为我们有四个方程(即四个约束条件),但有三个未知数(即三个自由量)。关于如何公式化求解列空间,我们将以后进行讲解,我们这里使用观察法求解。我们观察矩阵A的列分向量,我们发现有两个independent vector线性无关向量,例如我们只取第一列和第二列的列向量,而第三列的列向量可以用前面两个列向量线性表示。于是,我们用两个R4的向量的所有的线性组合便能构成列空间,列空间便被我们找到了。

我们对系数b构成的子空间——列空间研究完了,我们同时也会对解[x1, x2, x3]构成的子空间感兴趣,而对于解的子空间的研究,便是对Ax=0齐次线性方程组的研究,所有的解x便构成了零空间。我们同样使用观察法进行研究,易见[x1, x2, x3]取[0, 0, 0]方程组有解,而我们取c[1, 1, -1]也有解,于是我们找到了零空间,便是[1, 1, -1]的所有的线性组合。注意,这是R3的向量子空间,而上面那个是R4的向量子空间。

