【动态规划】子序列系列
文章目录
- 动态规划(子序列系列)
- 1. 最长递增子序列
- 2. 摆动序列
- 3. 最长递增子序列的个数
- 4. 最长数对链
- 5. 最长定差子序列
- 6. 最长的斐波那契子序列的长度
- 7. 最长等差数列
- 8. 等差数列划分 || - 子序列
动态规划(子序列系列)
1. 最长递增子序列
题目链接
-
状态表示
dp[i]表示到 i 位置时,所有子序列当中最长的子序列的长度 -
状态转移方程
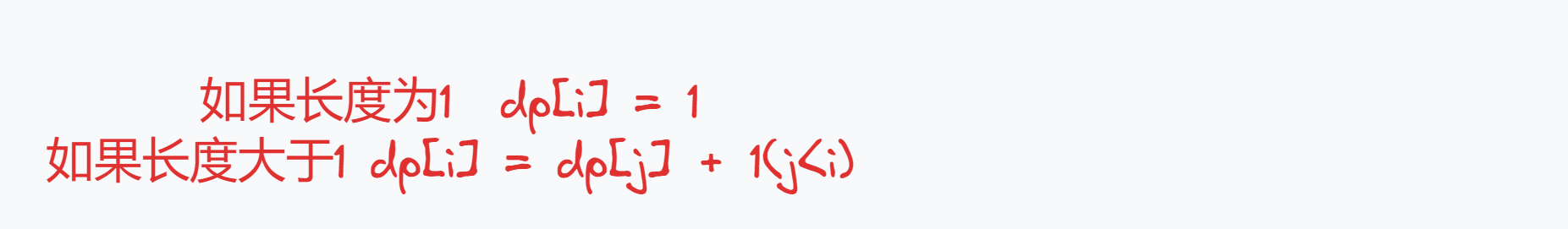
-
初始化
表中的所有数据初始化为1
-
填表
从左到右
-
返回值
返回整个dp表里面最大的值
AC代码:
class Solution
{
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n, 1);int ret = 1;for (int i = 1; i < n; i++){for (int j = 0; j < i; j++){if (nums[i] > nums[j]){dp[i] = max(dp[i], dp[j] + 1);}}ret = max(ret, dp[i]);}return ret;}
};
2. 摆动序列
题目链接
-
状态表示
f[i]表示:以 i 位置为结尾的所有子序列当中,最后一个位置是上升的最长摆动序列的长度g[i]表示:以 i 位置为结尾的所有子序列当中,最后一个位置是下降的最长摆动序列的长度 -
状态转移方程
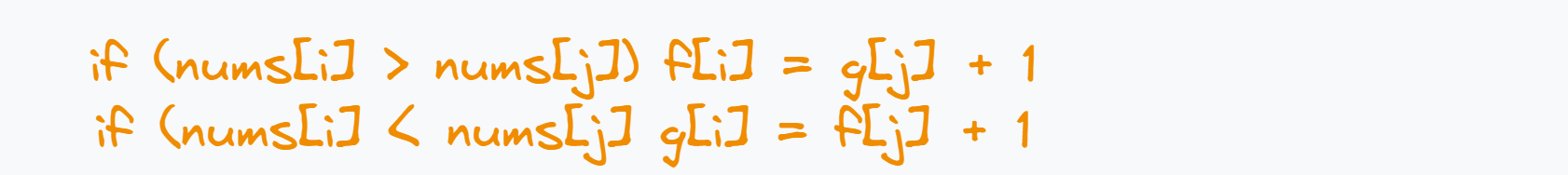
-
初始化
表中的所有值初始化为1
-
填表
从左到右
-
返回值
返回两个表中的最大值
AC代码:
class Solution
{
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();vector<int> f(n, 1), g(n, 1);int ret = 1;for (int i = 1; i < n; i++){for (int j = 0; j < i; j++){if (nums[i] > nums[j]) f[i] = max(f[i], g[j] + 1);else if (nums[i] < nums[j]) g[i] = max(g[i], f[j] + 1);}ret = max(ret, max(f[i], g[i]));}return ret;}
};
3. 最长递增子序列的个数
题目链接
这里需要用到一种思想:
如何一次遍历数组,就可以找到最大数出现的次数
代码实现:
#include <iostream>using namespace std;int main()
{int arr[] = {2, 3, 1, 234, 43, 342, 234, 5, 34, 43, 8, 342};int n = sizeof(arr)/sizeof(arr[0]);int maxval = 0;int count = 0;for (int i = 0; i < n; i++){if (arr[i] > maxval) maxval = arr[i], count = 1;else if (arr[i] == maxval) count++;}cout << maxval << endl;cout << count << endl;return 0;
}
-
状态表示
len[i]表示以 i 位置为结尾所有子序列当中,最长递增子序列的长度count[i]表示以 i 位置为结尾所有子序列当中,最长递增子序列的个数 -
状态转移方程
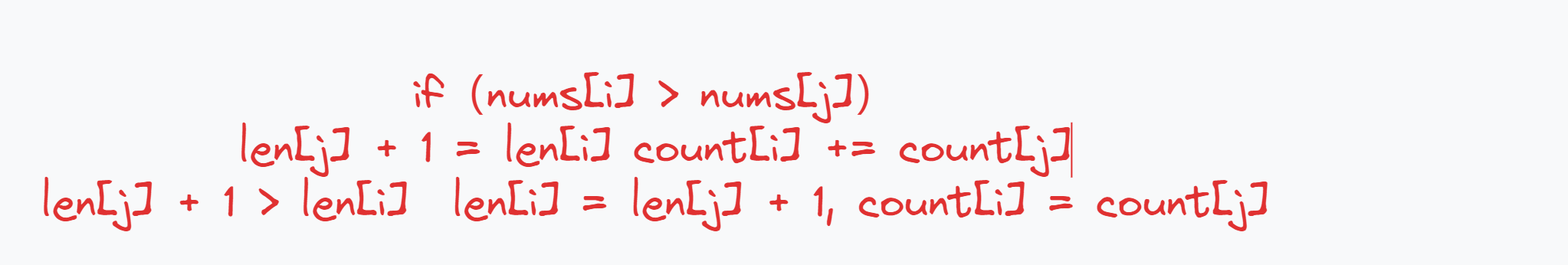
-
初始化
所有值都初始化为1
-
填表
从左到右
-
返回值
count表最后一个
AC代码:
class Solution
{
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> len(n, 1), count(n, 1);int retval = 1, retcount = 1;for (int i = 1; i < n; i++){for (int j = 0; j < i; j++){if (nums[i] > nums[j]){if (len[j] + 1 > len[i]) len[i] = len[j] + 1, count[i] = count[j];else if (len[j] + 1 == len[i]) count[i] += count[j];}}if (retval == len[i]) retcount += count[i];else if (retval < len[i]) retval = len[i], retcount = count[i];}return retcount;}
};
4. 最长数对链
题目链接
分析:状态表示以某个位置为结尾的时候,后面的元素不能影响当前的填表,但是这个题目已经影响打了,所有需要将数组排序
-
状态表示
dp[i]表示以 i 位置为结尾的所有数对链当中,最长的数对链的长度 -
状态转移方程
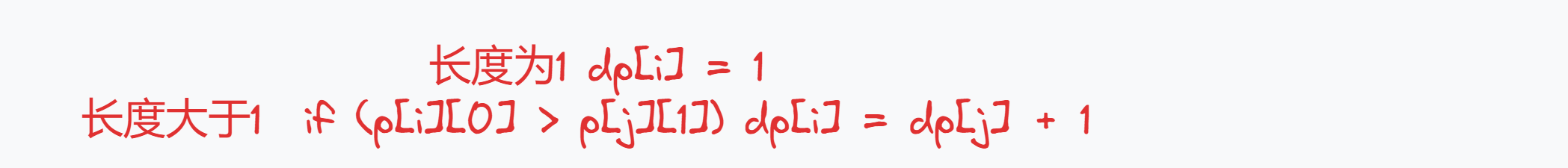
-
初始化
所有初始化为1
-
填表
从做到右
-
返回值
返回整个表的最大值
AC代码:
class Solution
{
public:int findLongestChain(vector<vector<int>>& pairs) {sort(pairs.begin(), pairs.end());int n = pairs.size();vector<int> dp(n, 1);int ret = 1;for (int i = 1; i < n; i++){for (int j = 0; j < i; j++){if (pairs[i][0] > pairs[j][1]) {dp[i] = max(dp[i], dp[j] + 1);}}ret = max(ret, dp[i]);}return ret;}
};
5. 最长定差子序列
题目链接
-
状态表示
dp[i]表示到 i 位置时,所有的子序列当中最长的定差子序列的长度 -
状态转移方程

-
初始化
将第一个元素对应的dp值初始化为1
-
填表
从左到右
-
返回值
返回整个dp表里的最大值
AC代码:
class Solution
{
public:int longestSubsequence(vector<int>& arr, int difference) {unordered_map<int, int> hash;hash[arr[0]] = 1;int ret = 1;for (int i = 1; i < arr.size(); i++){hash[arr[i]] = hash[arr[i] - difference] + 1;ret = max(ret, hash[arr[i]]);}return ret;}
};
6. 最长的斐波那契子序列的长度
题目链接
-
状态表示
dp[i][j]表示以 i j 为结尾的所有子序列当中,最长的斐波那契数列的长度 -
状态转移方程

优化:将数组的元素和下标绑定,方便查找
-
初始化
-
填表
-
返回值
返回值可能小于3, 这是应该返回0
AC代码:
class Solution
{
public:int lenLongestFibSubseq(vector<int>& arr) {int n = arr.size();unordered_map<int, int> hash;for (int i = 0; i < n; i++) hash[arr[i]] = i;vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;for (int j = 2; j < n; j++) // 固定最后一个位置{for (int i = 1; i < j; i++){int a = arr[j] - arr[i];if (a < arr[i] && hash.count(a)){dp[i][j] = dp[hash[a]][i] + 1;}ret = max(ret, dp[i][j]);}}return ret < 3 ? 0 : ret;}
};
7. 最长等差数列
题目链接
-
状态表示
dp[i][j] 表示 以 i j 为结尾的所有子序列当中最长的等差子序列的长度 -
状态转移方程

优化:一边dp一边保存离它最近元素的下标,当 i 位置填完之后将它填入哈希表中即可。所以需要先固定第倒数第二个元素,接着固定倒数第一个元素
-
初始化
-
填表
-
返回值
返回是整个dp表里的最大值
AC代码:
class Solution
{
public:int longestArithSeqLength(vector<int>& nums) {unordered_map<int, int> hash;int n = nums.size();hash[nums[0]] = 0;vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;for (int i = 1; i < n; i++){for (int j = i + 1; j < n; j++){int a = 2 * nums[i] - nums[j];if (hash.count(a)){dp[i][j] = dp[hash[a]][i] + 1;}ret = max(ret, dp[i][j]);}hash[nums[i]] = i;}return ret;}
};
8. 等差数列划分 || - 子序列
题目链接
-
状态表示
dp[i][j]表示以 i j 为是等差数列的子序列的个数 -
状态表示

-
初始化
-
填表
-
返回值
AC代码:
class Solution
{
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();unordered_map<long long, vector<int>> hash;for (int i = 0; i < n; i++) hash[nums[i]].push_back(i);vector<vector<int>> dp(n, vector<int>(n));int sum = 0;for (int j = 2; j < n; j++) // 固定倒数第一个{for (int i = 1; i < j; i++){long long a = (long long)nums[i] * 2 - nums[j];if (hash.count(a)){for (auto k : hash[a]){if (k < i) dp[i][j] += dp[k][i] + 1;else break;}}sum += dp[i][j];}}return sum;}
};
