算法题--二叉树(二叉树的最近公共祖先、重建二叉树、二叉搜索树的后序遍历序列)
目录
二叉树
题目
二叉树的最近公共祖先
原题链接
解析
二叉搜索树的最近公共节点
核心思想
答案
重建二叉树
题目链接
解析
核心思想
答案
二叉搜索树的后序遍历序列
原题链接
解析
核心思想
答案
二叉树
该类题目的解决一般是通过节点的遍历去实现,一般是分两种。
一是递归(深度优先),该方法通常代码比较简单,难懂。首先需要确定入参和返回的内容,然后确定层级之间的关系,最后去找递归的出口。
二是广度优先(该方法一般只有可以分层次处理的才能用),该方法代码量多,易懂。首先借助数组存储第一层的节点,然后每次将数组中的节点分批从数组头部取出(当对比2个节点时就一次取2个),处理完后将对应的子节点分批再从数组尾部存入数组(注意需要对比的子节点相邻存入,这样取出正好配对)。递归上述步骤直到数组为空。
注意特殊的二叉树会满足一些条件。
题目
二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
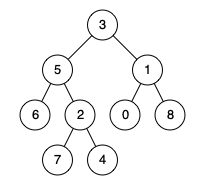
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点5和节点1的最近公共祖先是节点3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点5和节点4的最近公共祖先是节点5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
/*** Definition for a binary tree node.* function TreeNode(val) {* this.val = val;* this.left = this.right = null;* }*/
var lowestCommonAncestor = function(root, p, q) {};原题链接
力扣
解析
注意一些树的节点之间会有大小关系,更方便于解题,例如二叉搜索树,二叉搜索树的左节点(包括其子节点上的值)小于根节点,右节点(包括其子节点上的值)大于根节点。
例如类似题目
二叉搜索树的最近公共节点
力扣
核心思想
方法一(递归)
1.确定入参和出参,入参:1需要检索当前节点root,2需要检索当前的节点下是否有目标节点p、q;出参:返回的目标节点或最近公共节点。
2.确定上下层关系,当root的左右两边节点出现p和q时,当前节点为公共的父节点。当只有一个左右节点中只有一个节点为目标节点时,返回目标节点。
3.找出口,当root不存在、或者root为目标节点时,返回root。
方法二(广度优先+哈希表存储父节点):
1.首先用广度优先算法遍历每个接地那,构建一个哈希表存储子节点对应父节点的关系。
2.求出p的所有父节点放入集合中。
3.从q节点往上取所有父节点,直到有父节点在p的父节点集合中存在。
答案
方法一(递归)
var lowestCommonAncestor = function (root, p, q) {if (!root || root === p || root === q) return root;const left = lowestCommonAncestor(root.left, p, q);const right = lowestCommonAncestor(root.right, p, q);if(left && right){return root}else{return left||right}
};方法二(广度优先+哈希表存储父节点)
var lowestCommonAncestor = function(root, p, q) {let queue = [root],parent = new Map();while(queue.length && (!parent.has(p) || !parent.has(q))){const node = queue.shift();node.left && queue.push(node.left);node.right && queue.push(node.right);node.left && parent.set(node.left, node);node.right && parent.set(node.right,node);}let pSet = new Set(),node = p;pSet.add(node);while(parent.has(node)){pSet.add(parent.get(node));node = parent.get(node);}node = q;if(pSet.has(node)) return node;while(parent.has(node)){node = parent.get(node);if(pSet.has(node)) return node;}return null;
};重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1] Output: [-1]
/*** Definition for a binary tree node.* function TreeNode(val) {* this.val = val;* this.left = this.right = null;* }*/
var buildTree = function(preorder, inorder) {};题目链接
力扣
解析
前序遍历的顺序是根左右,中序遍历的顺序为左根右。
以示例1解释,[3,9,20,15,7]前序遍历的第一个值3一定为根的值,我们将它取出,前序遍历剩余[9,20,15,7]。
3在中序遍历[9,3,15,20,7]中的位置,可以分割出[9],[15,20,7],我们知道[9]一定是根3的左子树的中序遍历,[15,20,7]一定是根3的右子树的中序遍历。
核心思想
递归
1.确定入参和出参,入参:前序遍历的后续遍历的序列。出参:根据遍历返回的当前根节点。
2.确定上下层关系,每次根据前序找到根节点,根据根节点在中序中划分属于左右节点的部分。
f(p,q)={ val:xxx,left:f(pl,ql),right:f(pr,qr)}。
3.找出口,当preorder不存在时。
答案
递归
var buildTree = function(preorder, inorder) {if (!preorder.length) {return;}const val = preorder.shift()const index = inorder.findIndex(item => item === val)const left = inorder.slice(0, index)const right = inorder.slice(index + 1)return {val,left: buildTree(preorder.slice(0, index), left),right: buildTree(preorder.slice(index), right)}
};
二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5/ \2 6/ \1 3
示例 1:
输入: [1,6,3,2,5] 输出: false
示例 2:
输入: [1,3,2,6,5] 输出: true
/*** @param {number[]} postorder* @return {boolean}*/
var verifyPostorder = function(postorder) {};原题链接
力扣
解析
二叉搜索树的左节点(包括其子节点上的值)小于根节点,右节点(包括其子节点上的值)大于根节点。故二叉搜索树可以只根据一个顺序的序列结果就可以构造树。
核心思想
递归
1.确定入参和出参,入参:当前序列。
2.确定上下层关系,取序列最后一个节点为根节点,每次根据当前序列,找到第一个大于根节点的,该元素的左边应该全部小于根节点,右边应该全部大于根节点,满足的话对左右两边的序列进行递归,f(x)=f(x.left)&&f(x.right)。
3.找出口,当preorder不存在时结束。
答案
递归
var verifyPostorder = function(postorder) {if (postorder.length <= 2) {return true}const root = postorder.pop()let index = postorder.findIndex(num => num > root)index = index === -1 ? postorder.length : indexconst left = postorder.slice(0, index)const right = postorder.slice(index)if(!(left.every(num => num < root) && right.every(num => num > root))){return false}return verifyPostorder(left) && verifyPostorder(right)
};