【LeetCode】124.二叉树中的最大路径和
题目
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:

输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
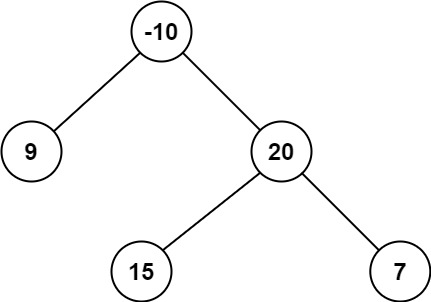
输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
- 树中节点数目范围是
[1, 3 * 104] -1000 <= Node.val <= 1000
解答
源代码
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {private int maxSum = Integer.MIN_VALUE;public int maxPathSum(TreeNode root) {maxGain(root);return maxSum;}public int maxGain(TreeNode root) {if(root == null) {return 0;}int left = Math.max(maxGain(root.left), 0);int right = Math.max(maxGain(root.right), 0);maxSum = Math.max(maxSum, root.val + left + right);return root.val + Math.max(left, right);}
}总结
这道题计算的二叉树的最大路径和对应的路径不一定经过根节点,所以递归函数计算的并不是最大根节点,而是当前节点的“最大贡献值”,也就是以这个节点为头的路径的最大路径和。
