Day46 算法记录| 动态规划 13(子序列)
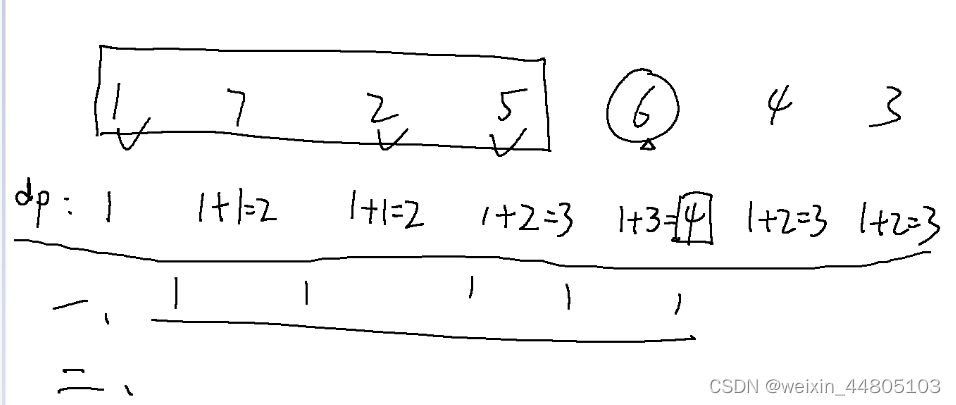
300.最长递增子序列
视频解析:
第一层for循环遍历每一个元素,
------- 第二层for循环找到当前元素前面有几个小于该值的元素
结尾需要统计最多的个数
class Solution {public int lengthOfLIS(int[] nums) {int n = nums.length;int[] dp = new int[n];//1.初始化Arrays.fill(dp,1);int res =1;for(int i=1;i<n;i++){//第二层for(int j=0;j<i;j++){if(nums[j]<nums[i]){dp[i] = Math.max(dp[i],dp[j]+1);}}res = Math.max(res,dp[i]);}return res;}
}
674. 最长连续递增序列
方法一:动态规划:dp[i]表示前面有几个连续小于当前位置的值
class Solution {public int findLengthOfLCIS(int[] nums) {int n = nums.length;int[] dp = new int[n];Arrays.fill(dp,1);int res =1;for(int i=1;i<n;i++){if(nums[i-1]<nums[i]){dp[i] = dp[i-1]+1;}res = Math.max(res,dp[i]);}return res;}
}
方法二:贪心
class Solution {public int findLengthOfLCIS(int[] nums) {int n = nums.length;int count =1;int res =1;for(int i=0;i<n-1;i++){if(nums[i]<nums[i+1]){count++;}else{count=1;}res = Math.max(res,count);}return res;}
}
718. 最长重复子数组
讲解的很好
class Solution {public int findLength(int[] A, int[] B) {int res =0;int[][] dp = new int[A.length+1][B.length+1];for(int i=1;i<=A.length;i++){for(int j =1;j<=B.length;j++){if(A[i-1] == B[j-1]){dp[i][j] = dp[i-1][j-1]+1;}res =Math.max(dp[i][j],res);}}return res;}
}
方法二:一维数组
因为当前元素依赖于(x-1,y-1),所以就需要从后向前去遍历
相当于在二维空间里面,从最后一行开始遍历
class Solution {public int findLength(int[] A, int[] B) {int res =0;int[] dp = new int[B.length+1];for(int i=1;i<=A.length;i++){ // 就像是商品for(int j =B.length;j>0;j--){if(A[i-1]==B[j-1]){dp[j] = dp[j-1]+1;}else{dp[j] =0;}res = Math.max(res,dp[j]);}}return res;}
}