【每日一题】2050. 并行课程 III
【每日一题】2050. 并行课程 III
- 2050. 并行课程 III
- 题目描述
- 解题思路
2050. 并行课程 III
题目描述
给你一个整数 n ,表示有 n 节课,课程编号从 1 到 n 。同时给你一个二维整数数组 relations ,其中 relations[j] = [prevCoursej, nextCoursej] ,表示课程 prevCoursej 必须在课程 nextCoursej 之前 完成(先修课的关系)。同时给你一个下标从 0 开始的整数数组 time ,其中 time[i] 表示完成第 (i+1) 门课程需要花费的 月份 数。
请你根据以下规则算出完成所有课程所需要的 最少 月份数:
如果一门课的所有先修课都已经完成,你可以在 任意 时间开始这门课程。
你可以 同时 上 任意门课程 。
请你返回完成所有课程所需要的 最少 月份数。
注意:测试数据保证一定可以完成所有课程(也就是先修课的关系构成一个有向无环图)。
示例 1:

输入:n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
输出:8
解释:上图展示了输入数据所表示的先修关系图,以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 和 2 。
课程 1 花费 3 个月,课程 2 花费 2 个月。
所以,最早开始课程 3 的时间是月份 3 ,完成所有课程所需时间为 3 + 5 = 8 个月。
示例 2:
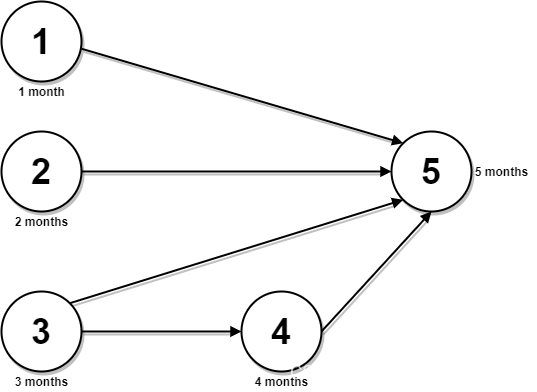
输入:n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出:12
解释:上图展示了输入数据所表示的先修关系图,以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ,2 和 3 。
在月份 1,2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始,也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1,2,3 和 4 之后开始,也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。
提示:
1 <= n <= 5 * 104
0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)
relations[j].length == 2
1 <= prevCoursej, nextCoursej <= n
prevCoursej != nextCoursej
所有的先修课程对 [prevCoursej, nextCoursej] 都是 互不相同 的。
time.length == n
1 <= time[i] <= 104
先修课程图是一个有向无环图。
解题思路
思路:使用二维数组g利用邻接表的方式建图,其中g[i]表示i的出边集合;使用一维数组deg表示节点的先驱个数;使用队列q表示入度为0的队列,并将deg[i]为0的节点加入队列;使用一维数组f表示完成该课程的最少月份数,当deg为0时,f=time,反之f=max(f…)+time。注意*max_element(f.begin(),f.end())求最大值。
class Solution {
public:int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {//建图 存储节点的邻接节点vector<vector<int>> g(n);//个数 统计节点的先行节点vector<int> deg(n);//建图 注意关系for(auto &r:relations){int x=r[0]-1,y=r[1]-1;g[x].push_back(y);deg[y]++;}//拓扑队列queue<int> q;for(int i=0;i<n;i++)if(deg[i]==0)q.push(i);vector<int> f(n);while(!q.empty()){int x=q.front();q.pop();//x出队意味着x的所有先修课都上完了f[x]+=time[x];for(int y:g[x]) //遍历x的邻居 注意y的先修课是x{f[y]=max(f[y],f[x]); //更新f[y]最大值 y的f值是其所有先修课的f值的最大值if(--deg[y]==0)q.push(y);}}return *max_element(f.begin(),f.end());}
};
总结:拓扑排序!
