Games101学习笔记 - 变换矩阵基础
二维空间下的变换
缩放矩阵
缩放变换:
假如一个点(X,Y)。x经过n倍缩放,y经过m倍缩放,得到的新点(X1,Y1);那么新点和远点有如下关系,X1 = n*X, Y1 =m*Y写成矩阵就是如下形式
<1>均匀缩放
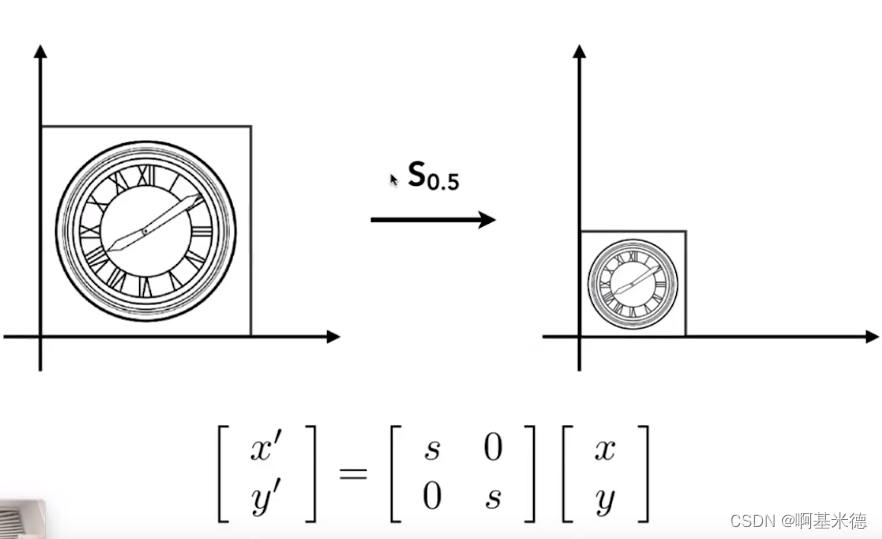
<2>不均匀缩放

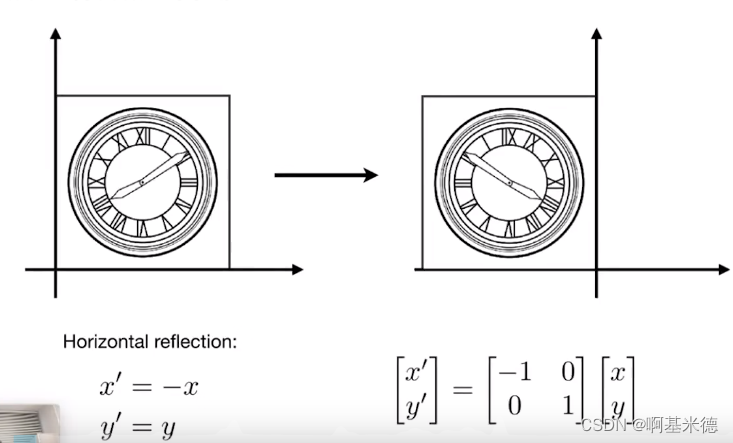
关于Y轴对阵矩阵
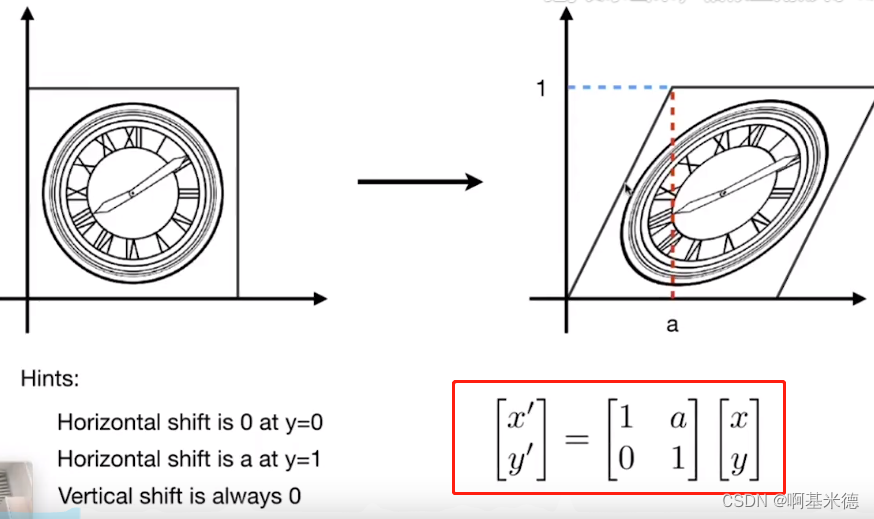
关于切变矩阵
关于旋转矩阵
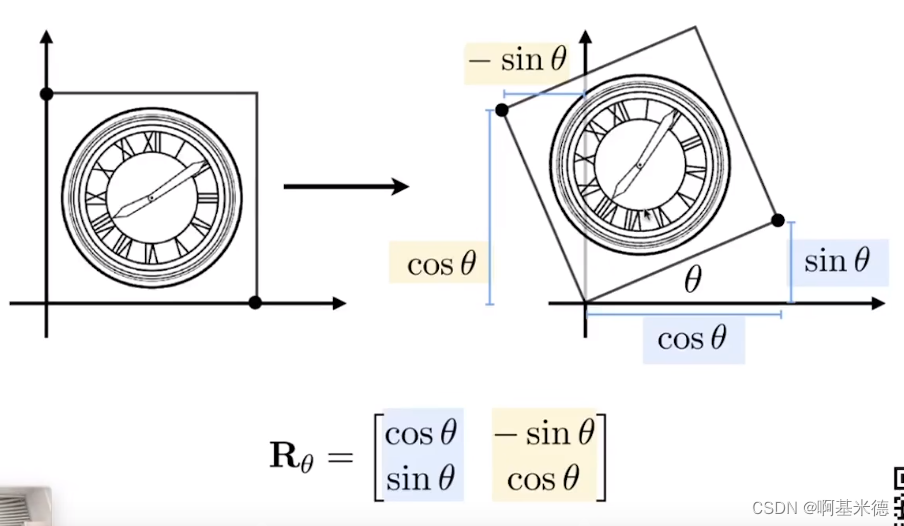
注意:上图是默认二维旋转的是以远点为圆转重心,并且逆时针旋转
旋转矩阵推导原理:
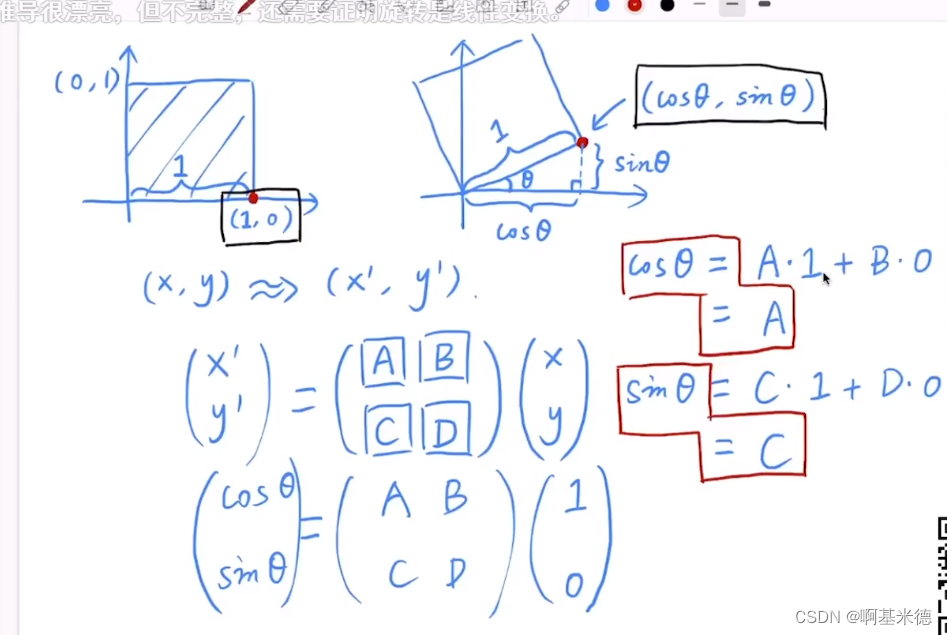
规律
对于任意的变换,变换后的点和变换前的点存在用变换前的点通过线性方程便是出来,都可以写成矩阵的形式,这种变换叫做线性变换
齐次坐标
引入原因:
上面说了ax + by 的方式都可以写成矩阵的形式,但是平移的操作的公式如下,不能写成矩阵的形式。
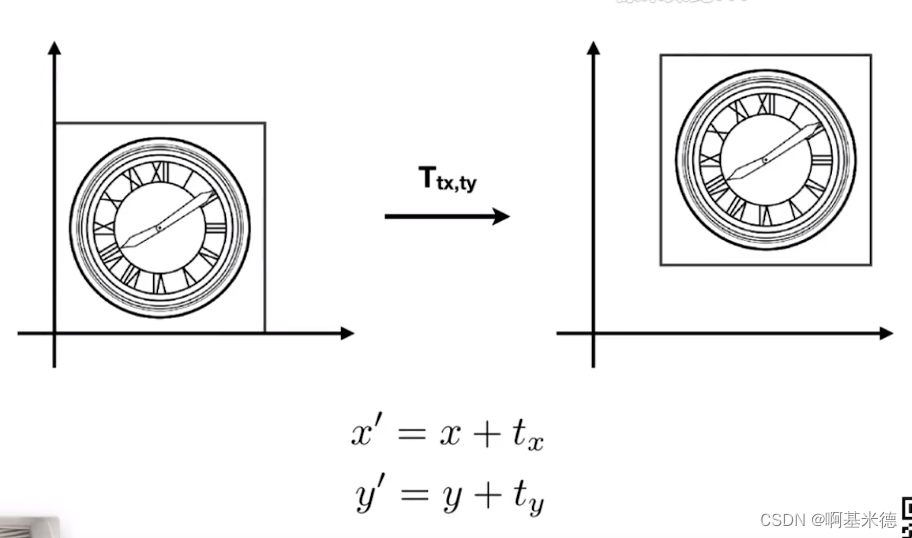
只能写成如下:
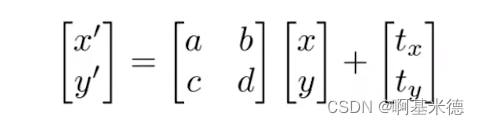
为了同意变换,让他们都写成一个矩阵和一个向量相乘的形式。我们引入了齐次坐标。
在其次坐标中:
已二维举例:
点会写成 (x,y,1)
向量会写成(x,y,0)
如下图引入后,平移矩阵可以写成如下形式:

至于引入后对于所有的仿射变化都可以根据引入的齐次坐标写成一个矩阵和一个向量相乘的形式
在齐次坐标的表示下各种变换矩阵就可以写成如下方式:

注意:
矩阵乘逆矩阵一定等于单位矩阵矩阵是从右向左计算的
三维空间中:
三维空间中齐次坐标表示:
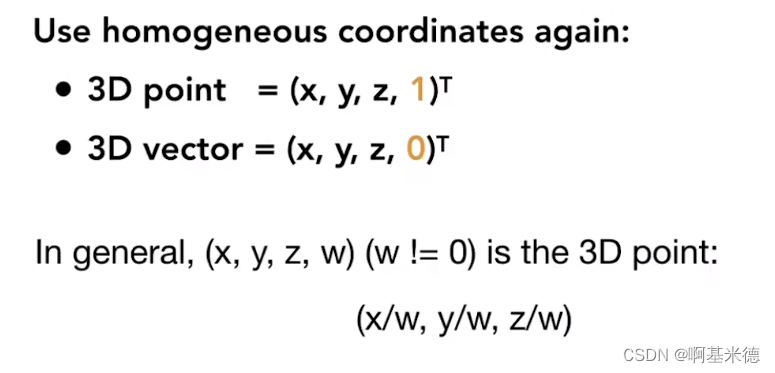
三维空间的仿射变换矩阵通常写成如下格式:

三维缩放矩阵:
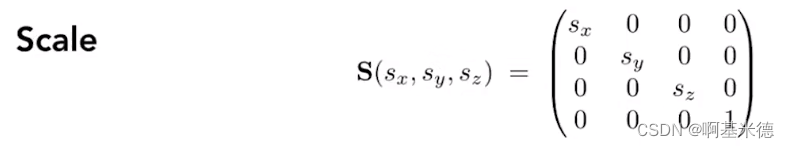
三维平移矩阵:
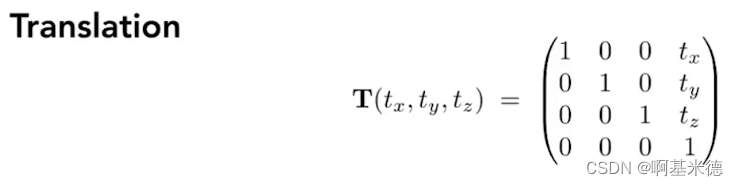
三维旋转矩阵:

注意:三维旋转都可以拆分为,绕X轴旋转,绕Y轴旋转和绕Z轴旋转,所以我们写出了这三种旋转变换矩阵
