【算法基础:搜索与图论】3.6 二分图(染色法判定二分图匈牙利算法)
文章目录
- 二分图介绍
- 染色法判定二分图
- 例题:860. 染色法判定二分图
- 匈牙利匹配
- 二分图最大匹配
- 匈牙利匹配算法思想
- 例题:861. 二分图的最大匹配
二分图介绍
https://oi-wiki.org/graph/bi-graph/
二分图是图论中的一个概念,它的所有节点可以被分为两个独立的集合,每个边的两个端点分别来自这两个不同的集合。
换句话说,二分图中不存在连接同一集合内两个节点的边。


染色法判定二分图
如何判断一个图是二分图?
当且仅当图中不含奇数环。(奇数环指的是环中边的个数是奇数)(因为每一条边都是从一个集合走到另一个集合,只有走偶数次才有可能回到同一个集合。)
染色:相邻的节点的颜色不一样。
因为没有奇数环,所以染色过程是一定不会发生矛盾的。
时间复杂度是 O ( n + m ) O(n + m) O(n+m) , n 表示点数,m 表示边数。
例题:860. 染色法判定二分图
https://www.acwing.com/activity/content/problem/content/926/
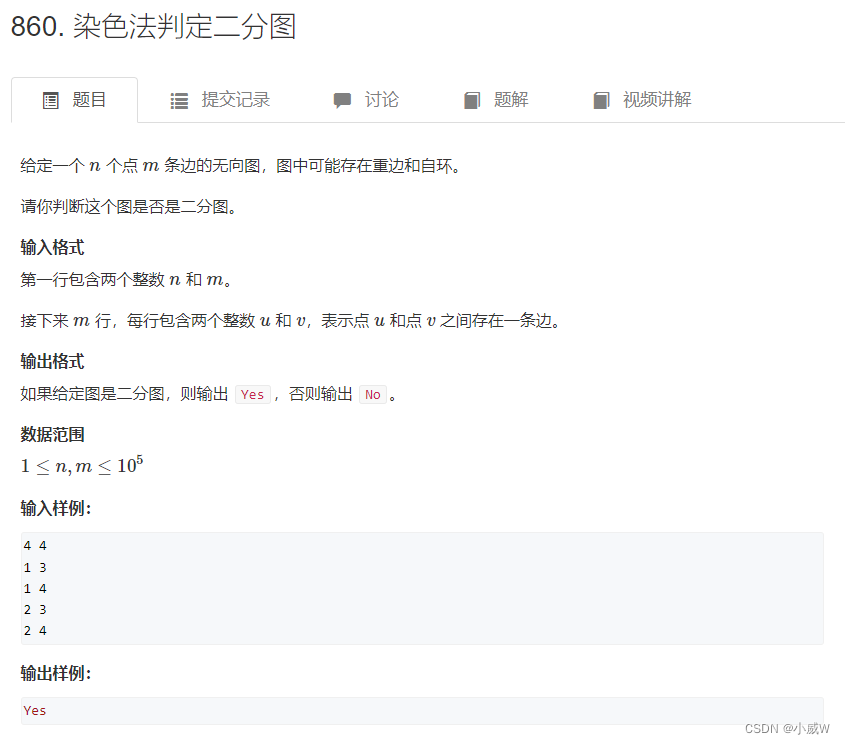
使用 dfs 对图中各个节点染色,染色过程中不发生冲突即为二分图。
import java.util.*;public class Main {static final int N = 100005;static List<Integer>[] g = new ArrayList[N];static int[] color = new int[N];public static void main(String[] args){Scanner sc = new Scanner(System.in);int n = sc.nextInt(), m = sc.nextInt();// 建图Arrays.setAll(g, e -> new ArrayList<Integer>());for (int i = 0; i < m; ++i) {int u = sc.nextInt(), v = sc.nextInt();g[u].add(v);g[v].add(u);}// 图可能由多个非连通的子图构成。因此,应该对每一个尚未访问过的点都进行一次深度优先搜索。boolean f = true;for (int i = 1; i <= n; ++i) {if (color[i] == 0 && !dfs(i, 1)) {f = false;break;}}System.out.println(f? "Yes": "No");}static boolean dfs(int x, int c) {boolean res = true;color[x] = c;for (int y: g[x]) {if (color[y] == 0) res &= dfs(y, 3 - c);else if (color[y] == color[x]) return false;}return res;}
}匈牙利匹配
二分图最大匹配
**二分图最大匹配**:
翻译成人话就是——
给定一个二分图 G,即分左右两部分,各部分之间的点没有边连接,要求选出一些边,使得这些边没有公共顶点,且边的数量最大。
匈牙利匹配算法思想
两个集合的点数分别是 n1 , n2。
枚举 n1 , 尝试 i 是否可以找到一个 j 完成匹配,匹配成功就 ++cnt。
所以重点是 find(i) 方法:
对每个 i ,枚举 i 相邻的所有 j —— 如果 j 没有被匹配就直接返回 true;如果 j 被匹配了,就尝试现在和 j 匹配的另一个 i 能不能换一个 j,能换就换一个然后返回 true;否则返回 false。
时间复杂度是 O ( n ∗ m ) O(n * m) O(n∗m),n 表示点数,m 表示边数。
例题:861. 二分图的最大匹配
https://www.acwing.com/activity/content/problem/content/927/

重点是理解数组 match 和 st 的含义,以及方法 find(x) 的写法和使用。
import java.util.*;public class Main {static final int N = 505;static int[][] g = new int[N][N];static int[] match = new int[N]; // match记录集合2中各个点匹配的集合1的点是哪个static boolean[] st = new boolean[N]; // st表示集合2中的点有没有被匹配static int n1, n2;public static void main(String[] args){Scanner sc = new Scanner(System.in);n1 = sc.nextInt();n2 = sc.nextInt();int m = sc.nextInt();// 建图for (int i = 0; i < m; ++i) {int u = sc.nextInt(), v = sc.nextInt();g[u][v] = 1; // 左边的 u 和 右边的 v 之间有一条边}int cnt = 0;for (int i = 1; i <= n1; ++i) {Arrays.fill(st, false); // 重置stif (find(i)) ++cnt;}System.out.println(cnt);}static boolean find(int x) {for (int j = 1; j <= n2; ++j) {if (!st[j] && g[x][j] == 1) {st[j] = true;// 如果 j 还没有匹配或者当前使用 j 的 x 可以让出去if (match[j] == 0 || find(match[j])) {match[j] = x;return true;}}}return false;}
}