神经网络:CNN中的filter,kernel_size,strides,padding对输出形状的影响
输入数据在经过卷积层后,形状一般会发生改变,而形状的变化往往与以下四个超参数有关。
1,filter(out_channel)
该超参数控制着输入数据经过卷积层中需要与几个卷积核进行运算,而输入数据与每个卷积核进行卷积运算后会产生一个二维矩阵,因此最后会产生 filter 个矩阵,分别分布在输出的各个通道中。故该超参数决定输出的通道数。
2,kernel_size(k)
卷积核的宽高一般来说是相等的,且都等于kernel_size,对应一个n x n x 3 (忽略样本轴)的输入数据,在经过卷积层后,输出的宽高 = 1 + (n - k) // s,双斜杠表示整除,s表示步幅strides。当n,k,s中的某个宽高不相等时,则输出的宽高需分别代入n, k, s的宽高进行计算。
3,strides(s)
步幅的大小决定了视野域(卷积核的形状映射在输入数据上的窗口)每次移动的距离,输出的宽高符合公式 1 + (n - k) // s。

4,padding
padding的设置在卷积运算之前就对元输入数据进行修改填充0,一般来说padding可取值VALID或SAME(pytorch中可分别对行列进行填充)。
①当取值为VALID时,则可用公式 1 + (n - k) // s 计算输出的宽高。
②当取值为SAME时,这时 k 的奇偶性就会影响到填充效果。
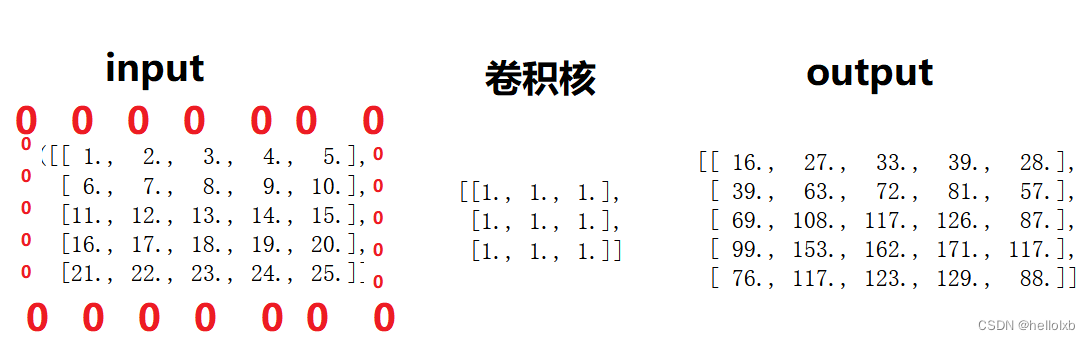
A:当 k 为奇数时,则上下左右都会填充 (k - 1) / 2 (可整除)个0行,故宽高可用公式 1 + (n + k - 1 - k) // s = 1 + (n - 1) // s(在Pytorch中,当 padding = SAME 时,s 必须等于1)。如下图(n = 5,k = 3,s = 1)
B:当k为偶数时,则上下左右都会填充(k - 1 - 1) / 2 = (k - 2)/ 2 个0行,然后下与右再填充1个0行,故宽高可用公式 1 + (n - k + k - 2 + 1) // s = 1 + (n - 1) // s 。如下图(n = 5,k = 2,s = 1)

综上所述:当取值为SAME时,输出的宽高可用公式 1 + (n - 1) // s 计算。
欢迎提问!
