独立成分分析ICA
独立成分分析 ICA
- 1. 算法原理简介
- 2.源信号与混合信号的差异
- 2.1 独立性 Independence
- 2.2 高斯性 Normality
- 2.3 复杂性 Complexity
- 3.非高斯性的度量
- 3.1 峭度 Kurtosis
- 参考文献
blind source separation (BSS)
1. 算法原理简介
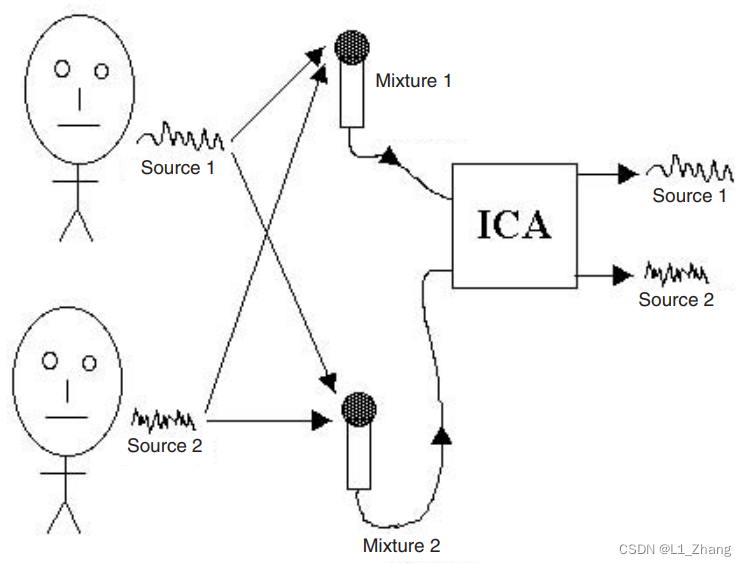
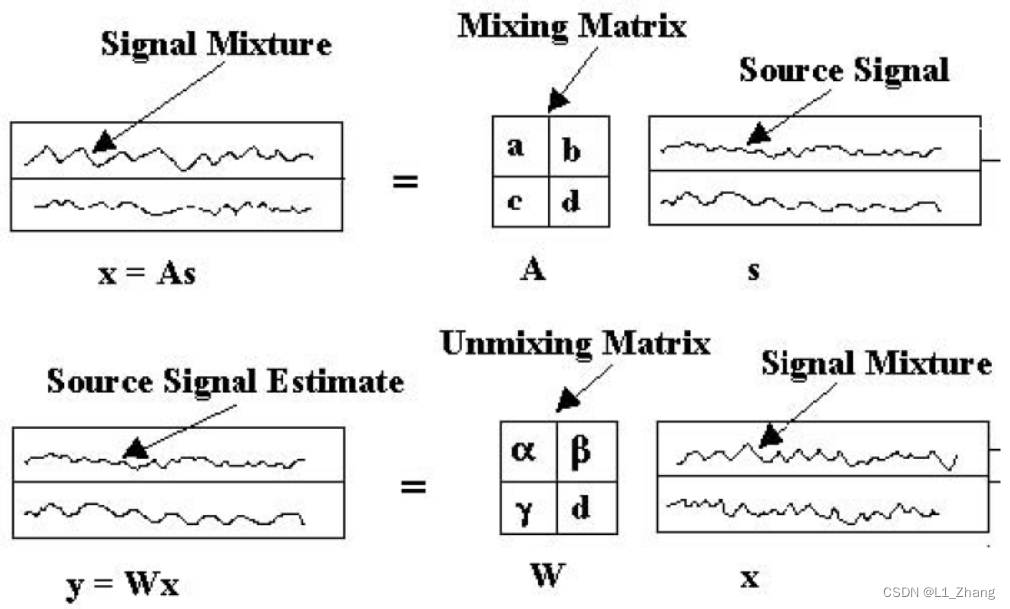
mixing得到signal mixture过程:
x 1 = a ∗ s 1 + b ∗ s 2 x 2 = c ∗ s 1 + d ∗ s 2 \qquad\qquad x_1=a*s_1+b*s_2 \\\qquad\qquad x_2=c*s_1+d*s_2 x1=a∗s1+b∗s2x2=c∗s1+d∗s2
即:
X = A ⋅ S \qquad\qquad X=A \cdot S X=A⋅S
unmixing获得独立源信号的过程:
s 1 = α ∗ x 1 + β ∗ x 2 s 2 = γ ∗ x 1 + δ ∗ x 2 \qquad\qquad s_1=\alpha*x_1+\beta*x_2 \\\qquad\qquad s_2=\gamma*x_1+\delta*x_2 s1=α∗x1+β∗x2s2=γ∗x1+δ∗x2
即:
S = W ⋅ X \qquad\qquad S=W \cdot X S=W⋅X
2.源信号与混合信号的差异
2.1 独立性 Independence
下图中,上半部分子图为两个源信号的幅值-时间曲线,下侧为两个混合信号的幅值-时间曲线.
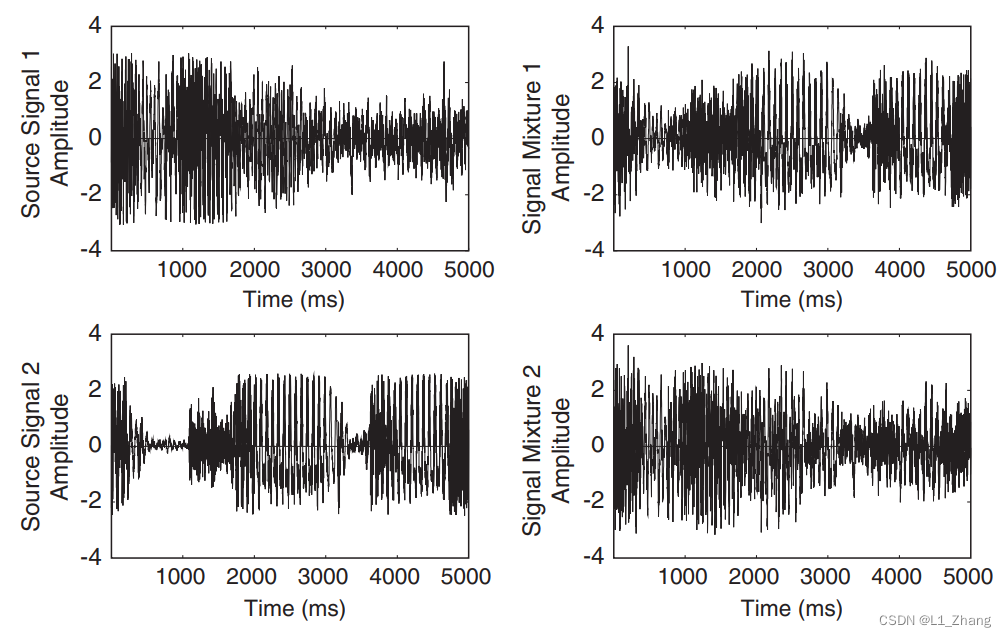
两个源信号、两个混合信号的幅值散点图(各时间点两个信号的幅值)分别显示如下:
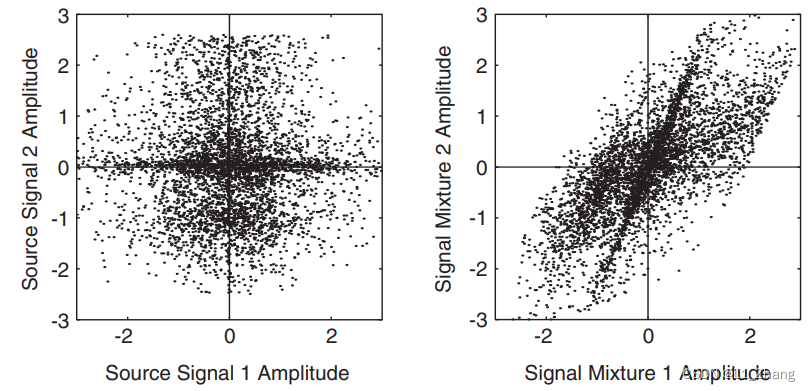
左图展示了源信号之间的独立性(互相之间没有贡献),而右图显示了混合信号幅值之间的正相关。
2.2 高斯性 Normality
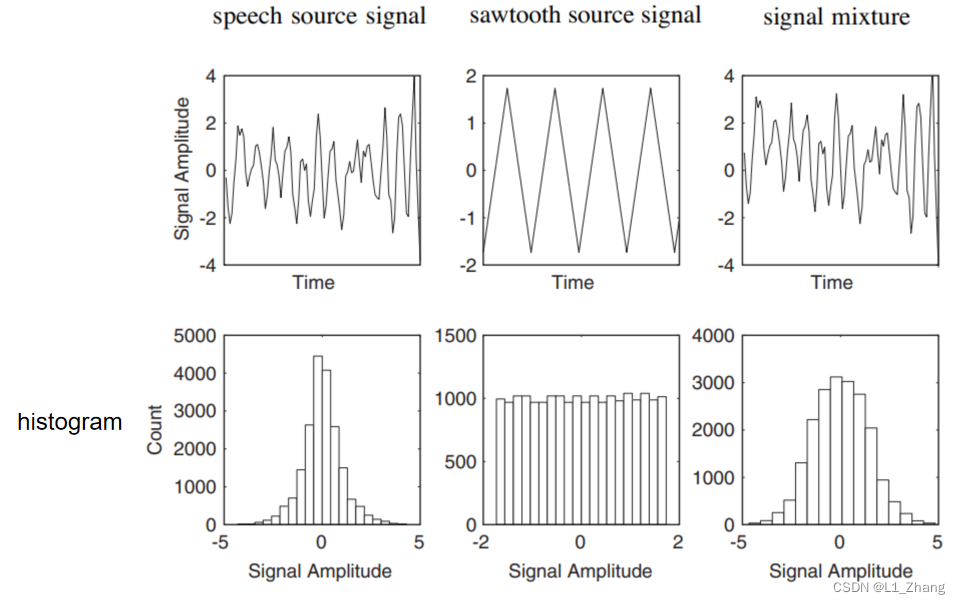
从上图可以看出,两个源信号的直方图为尖峰(peaky)或者平坦(flat)的,而它们的混合信号为bell-shaped,即具有高斯正态分布特征。
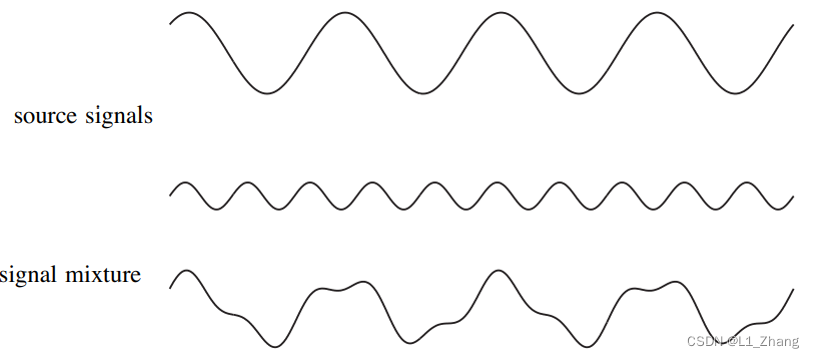
2.3 复杂性 Complexity
一般而言,源信号相对混合信号来说具有低复杂性。
3.非高斯性的度量
3.1 峭度 Kurtosis
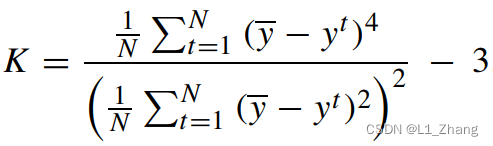
参考文献
[1] http://pzs.dstu.dp.ua/DataMining/ica/bibl/Stone.pdf
