算法基础学习笔记——④前缀和\差分\双指针\位运算
✨博主:命运之光
✨专栏:算法基础学习

目录
✨前缀和
✨一维前缀和
🍓一维前缀和模板:
✨二维前缀和
🍓二位前缀和模板:
前言:算法学习笔记记录日常分享,需要的看哈O(∩_∩)O,感谢大家的支持!
✨前缀和
✨一维前缀和
原i:a[1] a[2] a[3] …a[n]
前缀和:s[i]=a[1]+a[2]+…+a[i] s[0]=0(方便处理边界问题)
注:下标一定从1开始
1.如何求s[i]:
for(i=1;i<=n;j++)s[i]=s[i-1]+a[i]2.作用:(快)O(1)
快速求出原数组里一段数的和

🍓一维前缀和模板:
S[i] = a[1] + a[2] + ... a[i]a[l] + ... + a[r] = S[r] -S[l -1]✨二维前缀和


🍓二位前缀和模板:
S[i, j] = 第i行j列格子左上部分所有元素的和。
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] -S[x1 -1, y2] -S[x2, y1 -1] + S[x1 -1, y1 -1]



✨差分
差分实际是前缀和的逆运算
✨一维差分
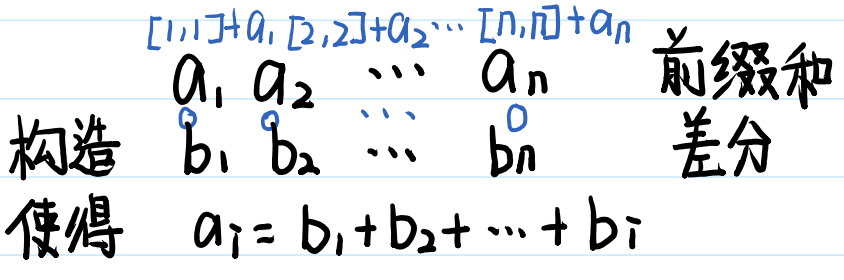

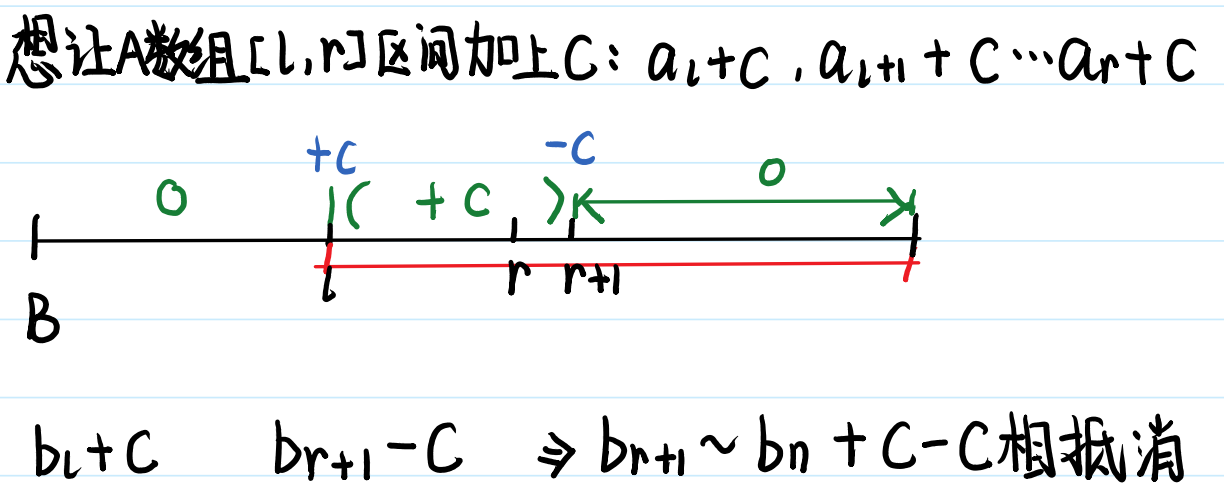
🍓一维差分模板:
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c

✨二维差分

🍓二维差分模板:
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

✨双指针
双指针算法的核心思想:
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
O(n^2)
将上面的朴素算法优化到O(n)

🍓双指针模板:
for (int i = 0, j = 0; i < n; i ++ )
{while (j < i && check(i, j)) j ++ ;// 具体问题的逻辑
}常见问题分类:
(1) 对于一个序列,用两个指针维护一段区间
(2) 对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作
🍓例题:统计日志
#include <iostream>
#include <algorithm>
using namespace std;
const int N=100000+5;
typedef struct Log{
int ts,id;
}Log;
Log logs[N];
//(tk-D,tk]
int n,d,k;
int cnt[N];//cnt[i]始终存储的是连续d分钟内id=i的帖子的点赞量
bool rt[N];
bool cmp(Log qian,Log hou){if(qian.ts<hou.ts)return true;return false;
}
int main(){scanf("%d%d%d",&n,&d,&k);int m=0;for(int i=1;i<=n;i++){scanf("%d%d",&logs[i].ts,&logs[i].id);m=max(m,logs[i].id);}sort(logs+1,logs+n+1,cmp); for(int i=1,j=1;i<=n;i++){//i和j始终维护长度小于d的区间 cnt[logs[i].id]++; while(logs[i].ts-logs[j].ts>=d){cnt[logs[j].id]--;j++;}if(cnt[logs[i].id]>=k){rt[logs[i].id]=true;}}for(int i=0;i<=m;i++){if(rt[i]==true)printf("%d\n",i);}
}🍓例题:统计子矩阵
#include <iostream>
using namespace std;
const int N=510;
int n,m,k;
int s[N][N];
int main(){cin>>n>>m>>k;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>s[i][j];s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+s[i][j];}}long long ans=0;for(int l=1;l<=m;l++){for(int r=l;r<=m;r++){for(int d=1,u=1;d<=n;d++){while(u<=d&&(s[d][r]-s[d][l-1]-s[u-1][r]+s[u-1][l-1]>k))u++;if(u<=d)ans+=d-u+1;}}}cout<<ans<<endl;
}✨位运算
✨操作一
n的二进制中第k位是几

1.先把第k位移到最后一位n>>k
2.看个位是几x&1


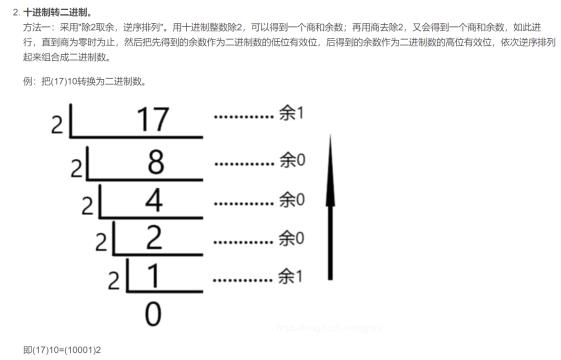
🍓十进制转化成二进制、八进制、十六进制(连除法)

🍓二进制、八进制、十六进制转化成十进制

🍓关于原码,反码,补码:
原码、反码和补码是计算机中用来表示带符号整数的三种编码方式。
1. 原码(Sign-Magnitude):
原码是最简单的表示方法,将一个整数按照正负号和数值进行编码。具体规则如下:
- 正数的原码是其二进制表示形式。
- 负数的原码是将对应的正数的原码最高位改为1。
🍓例如,假设用8位二进制表示整数,数字+3的原码是00000011,数字-3的原码是10000011。
2. 反码(One's Complement):
反码是在原码的基础上,将负数的表示方式进行改进。具体规则如下:
- 正数的反码与其原码相同。
- 负数的反码是将对应的正数的原码按位取反,即将0变为1,将1变为0。
🍓例如,数字+3的反码是00000011,数字-3的反码是11111100。
3. 补码(Two's Complement):
补码是在反码的基础上进行改进,是计算机中最常用的表示方式。具体规则如下:
- 正数的补码与其原码相同。
- 负数的补码是将对应的正数的原码按位取反,然后再加1。
🍓例如,数字+3的补码是00000011,数字-3的补码是11111101。
补码的使用在计算机中具有以下好处:
- 可以统一处理正数和负数的加减运算,无需单独处理符号位。
- 补码只有一个表示零的编码,避免了正零和负零的问题。
- 补码的表示范围比原码和反码更广,能够表示的最大正整数比较大。
🍓🍓需要注意的是,在使用补码表示的计算机系统中,最高位通常被用作符号位,即0表示正数,1表示负数。这种表示方式使得补码能够直接进行加减运算,并且可以方便地检测结果的正负。
