常微分方程ODE和Neural Ordinary Differential Equations
微分方程(英語:Differential equation,DE)是一種數學方程,用來描述某一類函数與其导数之间的关系。微分方程的解是一個符合方程的函數。而在初等数学的代数方程裡,其解是常数值。
常微分方程(英語:ordinary differential equation,簡稱ODE)是未知函数只含有一个自变量的微分方程。
很多科学问题都可以表示为常微分方程,例如根据牛顿第二运动定律,物体在力的作用下的位移 和时间 的关系就可以表示为如下常微分方程:

ODE solver是常微分方程的数值解法工具。它使用数值解法来近似求解常微分方程,得到近似的解。

从输入层 h(0) 开始,我们可以将输出层 h(T ) 定义为这个 ODE 初始值问题在某个时间 T 的解。该值可以由黑盒微分方程求解器计算。
给定z(t0)和f的参数,向前传播求解z(t1)很容易。(只需要一个ODESolve)
但是用反向传播求L 关于 θ 的梯度,怎么求?

第一步是确定损失的梯度如何取决于每个时刻的隐藏状态 z(t)。这个量称为伴
随 a(t) = ∂L /∂z(t) 。它的动态由另一个 ODE 给出,
 (35)
(35)
我们指出了伴随方法和反向传播(等式 38)之间的相似性。类似于反向传播,伴随态的 ODE 需要及时向后求解。我们在最后一次指定为约束点,就是最后一个时间点的loss的梯度,可以得到关于任何时候的隐藏状态,

t为tN的时候,∂f(z(t), t, θ) /∂z(t)的计算方法和其他时间点没有区别,只是把t的值换成tN而已。我们只需要把z(tN)和tN输入到f中,然后用自动微分的方法求出f对z(tN)的偏导数就可以了。
扩展上面的方法,推广可以得到关于 θ 的梯度

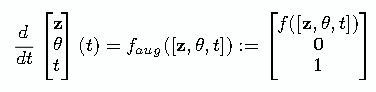

f 的雅可比行列式(指f对它的输入变量的偏导数组成的矩阵)具有以下形式
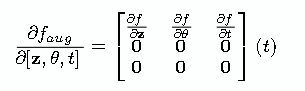 结合(35)
结合(35)


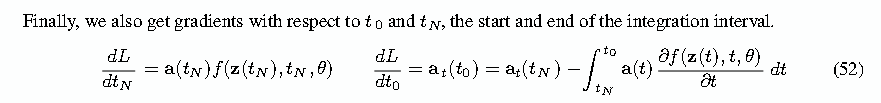


 算法1的目的是计算一个常微分方程初值问题的反向模式导数,也就是损失函数对参数的梯度
算法1的目的是计算一个常微分方程初值问题的反向模式导数,也就是损失函数对参数的梯度







