概率论:样本与总体分布,Z分数与概率
参考书目:《行为科学统计精要》(第八版)——弗雷德里克·J·格雷维特
数据及其样本的分布
描述一组数据分布
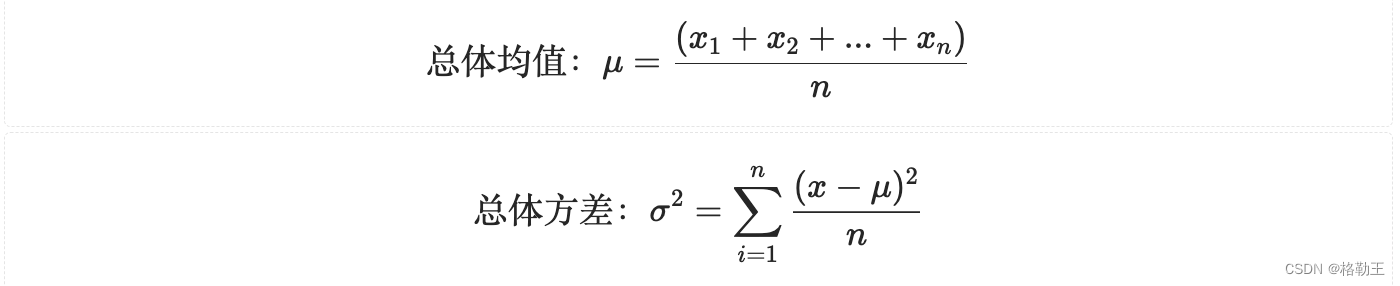
描述一组样本数据的分布
描述样本数据的均值和整体数据一样,但是样本标准差的公式除以了n-1,这里引入自由度的概念
自由度:如果均值确定,那么n个数据组成的样本中,只有n-1个数据的取值是自由的,最后一个数据等于n*均值减去其余n-1个值的和
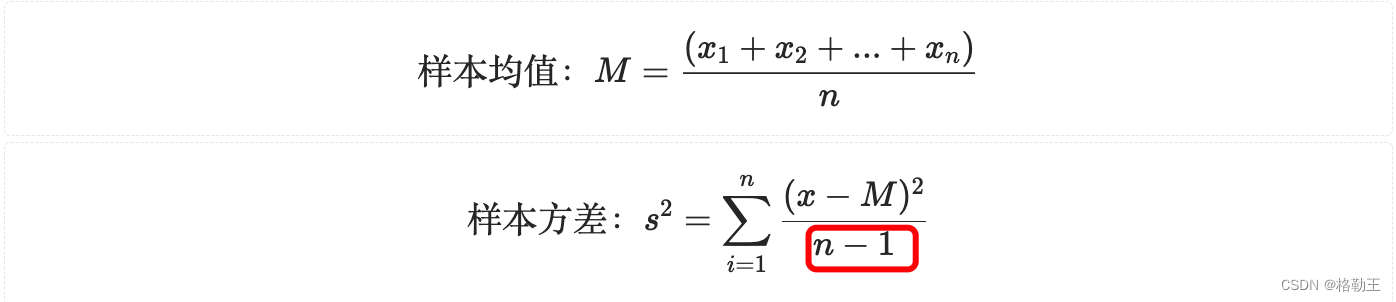
Z分位数
Z分位数描述的是一个数据在整组数据中的位置:即:当前值x距离总体均值有多少个标准差的距离

Z分位数因为是描述分布位置的,所以我们通常在去量纲单位(标准化为0-1的分布)的处理中经常用到,因为不管数据单位是时分秒,十万百万千万,在观测某个数值在整体分布中的位置,衡量标准都是一样的,不受单位影响。
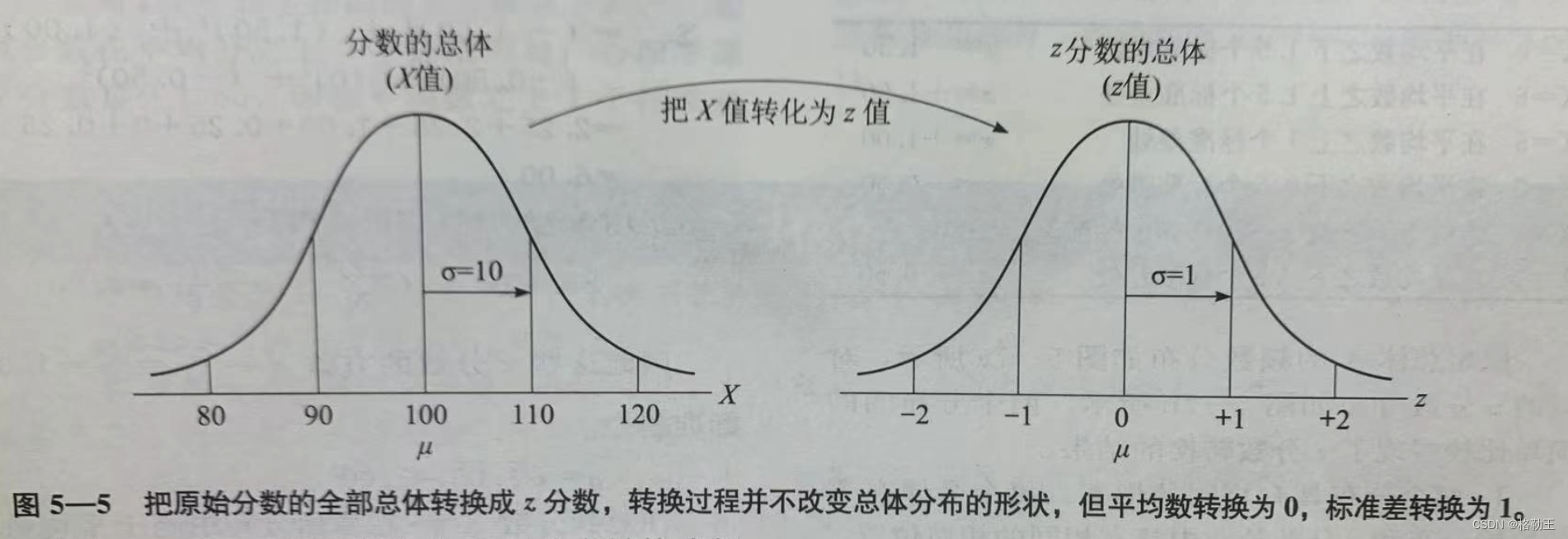
Z分位数可以帮助判断一个样本是不是异常值,也就是根据一个数据在整组数据中的Z分位数值,对应找到这个数据在整组数据中出现的概率,具体数值参考标准正态分布表,如下图

也就是说,如果Z分位数大于1.96,那么数据出现的概率小于1-97.5%=2.5%,对应的因为是标准正态分布,所以Z分位数小于1.96,对应数据出现的概率也是同样小于2.5%
总体和样本
如果Z分位数衡量的是,一个数值在整体数值中出现的概率大小。换句话说Z分位数可以表示,这个数值是能代表整体的,还是说是个异常值
那么,按照这个思路,我们如何衡量在一个整体中随机挑选N个数值组成的样本是否能代表整体
我们直观感受,影响这个结论的因素有三点:
1、样本均值和总体均值是否相近(M-μ),越相近说明越能代表总体
2、总体分布方差,总体数据的离散度越小选中的样本越有代表性,极端情况总体数据都是一样的值,那么无论怎么选,样本分布都和总体分布一致
3、样本量大小(n),样本量越大越能体现整体,极端情况样本量最大等于整体数据量
将以上三个因素结合Z分位数的计算思路,我们引出样本Z分位数
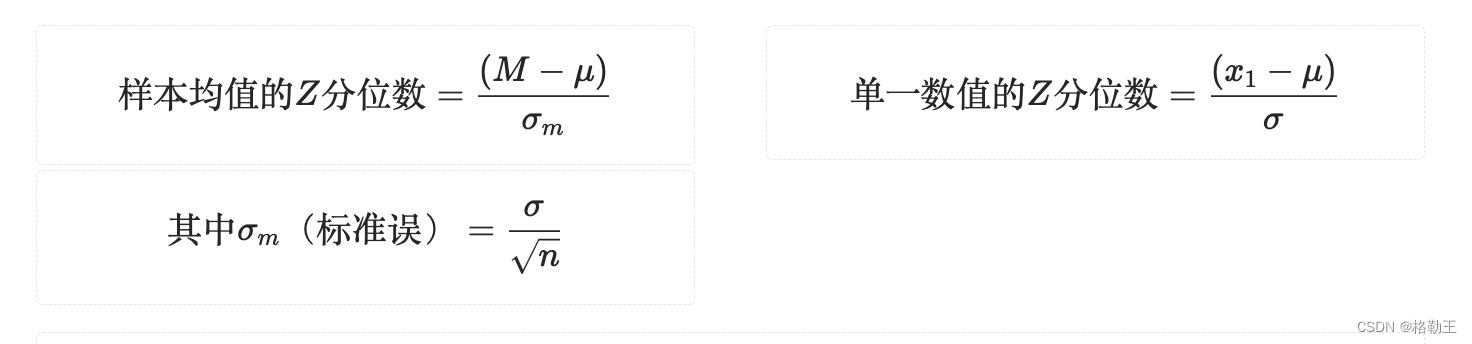
如果Z分位数过大或者过小,那么说明不大可能从总体中抽中这样的样本。
