✨博主：命运之光
✨专栏：算法基础学习

目录

 ✨最小生成树 

🍓朴素Prim

🍓Kruskal算法

✨二分图

🍓匈牙利算法

 ✨质数

🍓（1）质数的判定——试除法

🍓（2）分解质因数——试除法

✨约数

🍓（1）试除法求一个数的所有约数

🍓（2）约数个数

🍓（3）约数之和

🍓（4）欧几里得算法（辗转相除法）

---

前言：算法学习笔记记录日常分享，需要的看哈O(∩_∩)O，感谢大家的支持！

---

 ✨最小生成树 

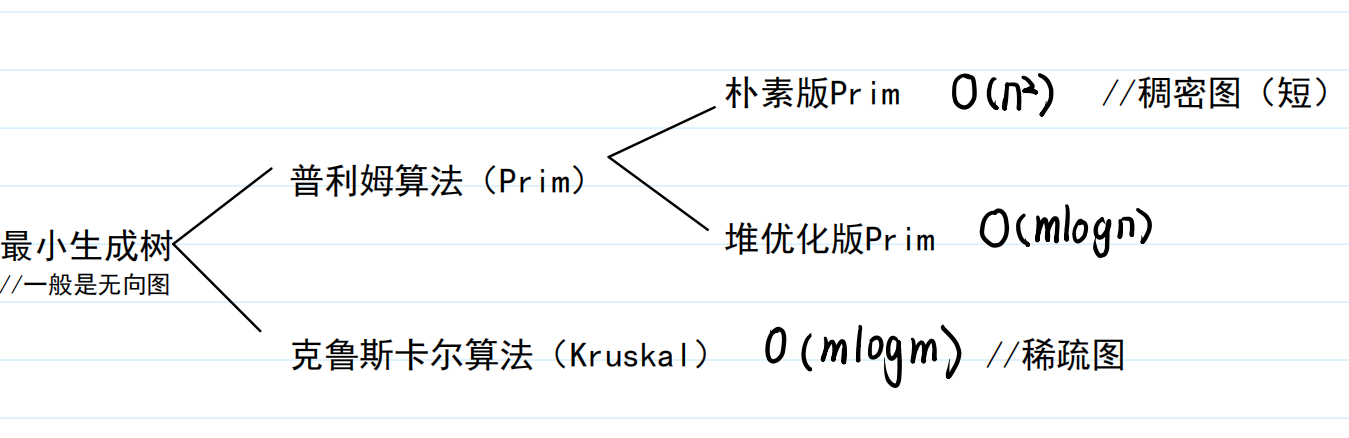
🍓朴素Prim

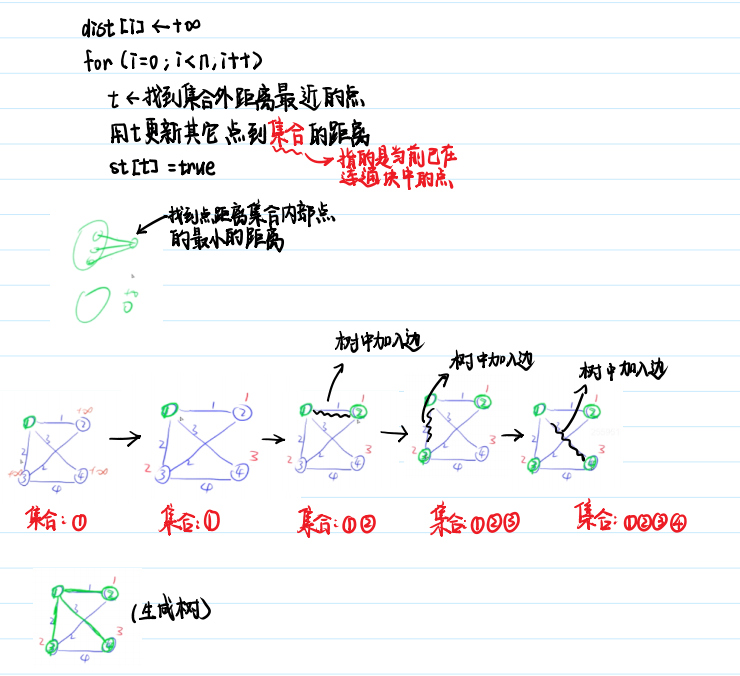
🍓朴素版prim算法：

时间复杂度是 O(n2+m)O(n2+m), nn 表示点数，mm 表示边数

int n; // n表示点数
int g[N][N]; // 邻接矩阵，存储所有边
int dist[N]; // 存储其他点到当前最小生成树的距离
bool st[N]; // 存储每个点是否已经在生成树中
// 如果图不连通，则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{memset(dist, 0x3f, sizeof dist);int res = 0;for (int i = 0; i < n; i ++ ){int t = -1;for (int j = 1; j <= n; j ++ )if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;if (i && dist[t] == INF) return INF;if (i) res += dist[t];st[t] = true;for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);}return res;
}

🍓Kruskal算法

Kruskal算法：

时间复杂度是 O(mlogm)O(mlogm), nn 表示点数，mm 表示边数

int n, m; // n是点数，m是边数
int p[N]; // 并查集的父节点数组
struct Edge // 存储边
{int a, b, w;bool operator< (const Edge &W)const{return w < W.w;}
}edges[M];
int find(int x) // 并查集核心操作
{if (p[x] != x) p[x] = find(p[x]);return p[x];
}
int kruskal()
{sort(edges, edges + m);for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集int res = 0, cnt = 0;for (int i = 0; i < m; i ++ ){int a = edges[i].a, b = edges[i].b, w = edges[i].w;a = find(a), b = find(b);if (a != b) // 如果两个连通块不连通，则将这两个连通块合并{p[a] = b;res += w;cnt ++ ;}}if (cnt < n - 1) return INF;return res;
}

✨二分图

染色法

判断一个图是不是二分图

二分图：可以把所有点分成两边，使所有边在集合之间，集合内部没有边。

二分图当且仅当图中不含奇数环

🍓染色法判别二分图：

时间复杂度是 O(n+m)O(n+m), nn 表示点数，mm 表示边数

int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储图
int color[N]; // 表示每个点的颜色，-1表示未染色，0表示白色，1表示黑色
// 参数：u表示当前节点，c表示当前点的颜色
bool dfs(int u, int c)
{color[u] = c;for (int i = h[u]; i != -1; i = ne[i]){int j = e[i];if (color[j] == -1){if (!dfs(j, !c)) return false;}else if (color[j] == c) return false;}return true;
}
bool check()
{memset(color, -1, sizeof color);bool flag = true;for (int i = 1; i <= n; i ++ )if (color[i] == -1)if (!dfs(i, 0)){flag = false;break;}return flag;
}

🍓匈牙利算法

🍓匈牙利算法：

时间复杂度是 O(nm)O(nm), nn 表示点数，mm 表示边数

int n1, n2; // n1表示第一个集合中的点数，n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx; // 邻接表存储所有边，匈牙利算法中只会用到从第一个集合指向第二个集合的边，所以这里只用存一个方向的边
int match[N]; // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N]; // 表示第二个集合中的每个点是否已经被遍历过
bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}
// 求最大匹配数，依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{memset(st, false, sizeof st);if (find(i)) res ++ ;
}

 ✨质数

🍓所有大于1的自然数，所有<=1的数既不是质数也不是合数

定义：在大于1的整数中，如果只包含1和本身这两个约数，就被称为质数，或者叫素数

🍓（1）质数的判定——试除法

质数的一个重要性质：如果d能整除n,显然n除d也能整除n

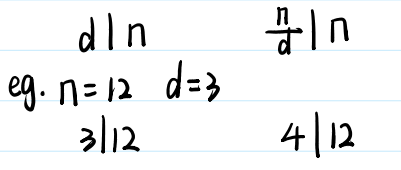
故发现n的所有的约数都是成对出现的（d与n/d都成成对出现的）

所以枚举时可以只枚举每一对当中较小的那一个，枚举：

🍓试除法判定质数：

bool is_prime(int x)
{if (x < 2) return false;for (int i = 2; i <= x / i; i ++ )if (x % i == 0)return false;return true;
}

🍓（2）分解质因数——试除法

从小到大枚举所有数

🍓试除法分解质因数：

void divide(int x)
{for (int i = 2; i <= x / i; i ++ )if (x % i == 0){int s = 0;while (x % i == 0) x /= i, s ++ ;cout << i << ' ' << s << endl;}if (x > 1) cout << x << ' ' << 1 << endl;cout << endl;
}

🍓筛

罗列出每个数，依次删除每个数的倍数，剩下的数就是质数，可以对此进行优化，可以不删每一个数的倍数， 可以只删质数的倍数，这样就不用重复删。

🍓质数定理：

优化完的筛法：埃氏筛法

🍓朴素筛法求素数：

int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (st[i]) continue;primes[cnt ++ ] = i;for (int j = i + i; j <= n; j += i)st[j] = true;}
}

🍓线性筛法：

把每一个合数用它的某个质因子筛掉

每个数都会被其最小质因子筛掉，而且每个数只有一个最小质因子，故每个数只会被筛一次

🍓线性筛法求素数：

int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[cnt ++ ] = i;for (int j = 0; primes[j] <= n / i; j ++ ){st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}
}

✨约数

约数

🍓（1）试除法求一个数的所有约数

🍓试除法求所有约数：

vector<int> get_divisors(int x)
{vector<int> res;for (int i = 1; i <= x / i; i ++ )if (x % i == 0){res.push_back(i);if (i != x / i) res.push_back(x / i);}sort(res.begin(), res.end());return res;
}

🍓（2）约数个数

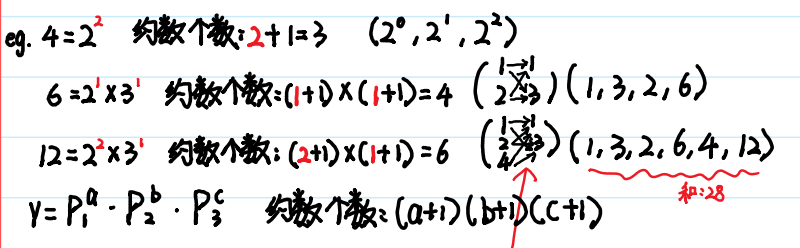
🍓（3）约数之和

约数个数和约数之和：

如果 N = p1^c1 * p2^c2 * ... *pk^ck

约数个数： (c1 + 1) * (c2 + 1) * ... * (ck + 1)

约数之和： (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)

🍓（4）欧几里得算法（辗转相除法）

🍓欧几里得算法：

int gcd(int a, int b)
{return b ? gcd(b, a % b) : a; // <表达式1>?<表达式2>:<表达式3>，
} //它的意思是，如果表达式1成立，则输出表达式2的值，否则输出表达式3的值

补充小知识：

两个数的积等于它们最大公约数和它们最小公倍数的

积。公式表示为 ：a×b=gcd(a,b)×lcm(a,b)

🍓最小公倍数与最大公约数模板：