当前位置：首页 > news >正文

[足式机器人]Part3机构运动微分几何学分析与综合Ch01-4 平面运动微分几何学——【读书笔记】

news 2025/7/1 2:21:07

本文仅供学习使用
本文参考：
《机构运动微分几何学分析与综合》-王德伦、汪伟
《微分几何》吴大任

Ch01-4 平面运动微分几何学

- - 1.2.3-2 点轨迹的Euler-Savary公式
  - 1.2.4 高阶曲率理论

1.2.3-2 点轨迹的Euler-Savary公式

例1-7：平面曲柄摇杆机构的 Euler-Savary公式。
在例1-5中给出了平面曲柄摇杆机构动瞬心线 $πm{{\pi }_{m}}$ 与定瞬心线 $πf{{\pi }_{f}}$ ，动瞬心线 $πm{{\pi }_{m}}$ 上的Frenet标架 ${R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}$ 可由式（1.47）得到∶
${R⃗m=1ka−θ˙(−sin⁡θi⃗m+cos⁡θj⃗m)E⃗1m=−[θ˙(ka−θ˙)cos⁡θ+θ¨sin⁡θ]i⃗m+[−θ˙(ka−θ˙)sin⁡θ+θ¨cos⁡θ]j⃗m[θ˙2(ka−θ˙)2+θ¨2]12E⃗2m=[θ˙(ka−θ˙)sin⁡θ−θ¨cos⁡θ]i⃗m−[θ˙(ka−θ˙)cos⁡θ+θ¨sin⁡θ]j⃗m[θ˙2(ka−θ˙)2+θ¨2]12\left\{ \begin{matrix} {{{\vec{R}}}_{m}}=\frac{1}{{{k}_{a}}-\dot{\theta }}(-\sin \theta {{{\vec{i}}}_{m}}+\cos \theta {{{\vec{j}}}_{m}}) \\ {{{\vec{E}}}_{1m}}=\frac{-[\dot{\theta }({{k}_{a}}-\dot{\theta })\cos \theta +\ddot{\theta }\sin \theta ]{{{\vec{i}}}_{m}}+[-\dot{\theta }({{k}_{a}}-\dot{\theta })\sin \theta +\ddot{\theta }\cos \theta ]{{{\vec{j}}}_{m}}}{{{[{{{\dot{\theta }}}^{2}}{{({{k}_{a}}-\dot{\theta })}^{2}}+{{{\ddot{\theta }}}^{2}}]}^{\frac{1}{2}}}} \\ {{{\vec{E}}}_{2m}}=\frac{[\dot{\theta }({{k}_{a}}-\dot{\theta })\sin \theta -\ddot{\theta }\cos \theta ]{{{\vec{i}}}_{m}}-[\dot{\theta }({{k}_{a}}-\dot{\theta })\cos \theta +\ddot{\theta }\sin \theta ]{{{\vec{j}}}_{m}}}{{{[{{{\dot{\theta }}}^{2}}{{({{k}_{a}}-\dot{\theta })}^{2}}+{{{\ddot{\theta }}}^{2}}]}^{\frac{1}{2}}}} \\ \end{matrix} \right.$
对于由 $r+Dsin⁡α=0r+D\sin \alpha =0$ 确定的连杆平面上的拐点圆，可以通过上式将其转换到连杆坐标系 ${B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}$ 中描述为∶
$(xm−a)2+(ym−b)2=D24{{({{x}_{m}}-a)}^{2}}+{{({{y}_{m}}-b)}^{2}}=\frac{{{D}^{2}}}{4}$
其中拐点圆圆心坐标 $(a, b)$ 为∶
${a=−θ¨cos⁡θ+(2ka−θ˙)(ka−θ˙)sin⁡θ2(ka−θ˙)3b=θ¨sin⁡θ+(2ka−θ˙)(ka−θ˙)cos⁡θ2(ka−θ˙)3\left\{ \begin{matrix} a=-\frac{\ddot{\theta }\cos \theta +(2{{k}_{a}}-\dot{\theta })({{k}_{a}}-\dot{\theta })\sin \theta }{2{{({{k}_{a}}-\dot{\theta })}^{3}}} \\ b=\frac{\ddot{\theta }\sin \theta +(2{{k}_{a}}-\dot{\theta })({{k}_{a}}-\dot{\theta })\cos \theta }{2{{({{k}_{a}}-\dot{\theta })}^{3}}} \\ \end{matrix} \right.$
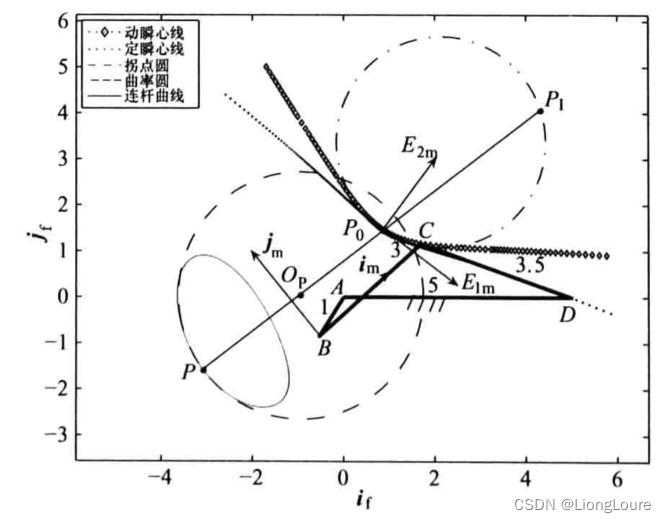
当该曲柄摇杆机构的输入角 $φ=238∘\varphi =238{}^\circ$ 时，瞬心点 ${{P}_{0}}$ 在连杆坐标系中的极坐标为 $rP0=2.6995,θP0=15.9604∘{{r}_{{{P}_{0}}}}=\text{2}\text{.6995},{{\theta }_{{{P}_{0}}}}=\text{15}\text{.9604}{}^\circ$ ，定瞬心线 $πf{{\pi }_{f}}$ 与动瞬心线 $πm{{\pi }_{m}}$ 的曲率分别为 $kf=0.3712,km=0.5892{{k}_{f}}=\text{0}\text{.3712,}{{k}_{m}}=\text{0}\text{.5892}$ ，从而诱导曲率 $k*=kf−km=−0.2180k\text{*=}{{k}_{f}}-{{k}_{m}}=-\text{0}\text{.2180}$ 。代人式（1.74b），得到此时的Euler-Savary公式为∶
$ρΓ(r−sin⁡α0.2180)=r2{{\rho }_{\Gamma }}\text{(}r-\frac{\sin \alpha }{\text{0}\text{.2180}}\text{)=}{{r}^{\text{2}}}$
此时连杆坐标系 ${B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}$ 中的拐点圆方程为∶
${{({{x}_{m}}-4.8075)}^{2}}+{{({{y}_{m}}-1.3502)}^{2}}=5.2627$
连杆上的一点 $P$ 在Frenet标架 ${R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}$ 中的极坐标为 $(5,250∘)(5,250{}^\circ )$ ，其在连杆坐标系 ${B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}$ 中的直角坐标为 $(- 2.3882, 1.1463)$ ，则可由Euler-Savary公式得到其轨迹曲线 $ΓP{{\Gamma }_{P}}$ ，在该瞬时的曲率半径 $ρΓ=2.6849{{\rho }_{\Gamma }}=2.6849$ ，从而可知曲率中心 ${{O}_{P}}$ 在Frenet标架 ${R⃗f;E⃗1f,E⃗2f}\{{{{\vec{R}}}_{f}};{{{\vec{E}}}_{1f}},{{{\vec{E}}}_{2f}}\}$ 中的极坐标（ $rOP=2.3151,αOP=250∘{{r}_{{{O}_{P}}}}=\text{2}\text{.3151},{{\alpha }_{{{O}_{P}}}}=\text{250}{}^\circ$ ），或者在固定坐标系 ${A;i⃗f,j⃗f}\{A;{{{\vec{i}}}_{f}},{{{\vec{j}}}_{f}}\}$ 中的直角坐标为 $(- 0.9384, 0.0349)$ 。此时，拐点 ${{P}_{I}}$ 在Frenet标架 ${R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}$ 中的极坐标为 $(4.3114,70∘)(4.3114,70{}^\circ )$ ，在连杆坐标系 ${B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}$ 中的直角坐标为 $(6.8928, 0.3940)$ 。将所有特征点的坐标均转换到固定坐标系中描述，结果如下图所示。

例1-8：平面曲柄滑块机构的Euler-Savary公式。
在例1-6中给出了平面曲柄滑块机构动瞬心线 $πm{{\pi }_{m}}$ 与定瞬心线 $πf{{\pi }_{f}}$ ，动瞬心线 $πm{{\pi }_{m}}$ 上的Frenet标架 ${R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}$ 可同样采用式（E1-7.1）得到。利用式（E1-7.2）和式（E1-7.3）可以得到连杆坐标系 ${B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}$ 中拐点圆的方程。
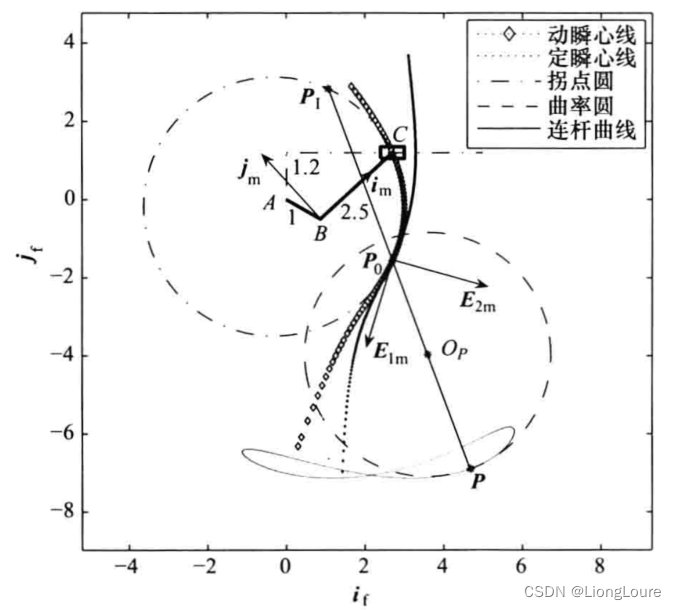
当曲柄滑块机构的输入角为 $φ=−30∘\varphi =-30{}^\circ$ 时，瞬心点 ${{P}_{0}}$ 在连杆坐标系中的极坐标为 $rP0=2.1166,θP0=−72.8463∘{{r}_{{{P}_{0}}}}=2.1166,{{\theta }_{{{P}_{0}}}}=-72.8463{}^\circ$ ，定瞬心线 $πf{{\pi }_{f}}$ 与动瞬心线 $πm{{\pi }_{m}}$ 的曲率分别为 ${{k}_{f}}=-0.1076,{{k}_{m}}=-0.2585$ ，从而诱导曲率 $k*=kf−km=0.1509k\text{*=}{{k}_{f}}-{{k}_{m}}=0.1509$ 。代入式（1.74b），得到此时的Euler-Savary公式∶
$ρΓ(r+sin⁡α0.1509)=r2{{\rho }_{\Gamma }}\text{(}r+\frac{\sin \alpha }{\text{0}\text{.1509}}\text{)=}{{r}^{\text{2}}}$
此时连杆坐标系 ${B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}$ 中的拐点圆方程为∶
${{({{x}_{m}}+0.6465)}^{2}}+{{({{y}_{m}}-1.0372)}^{2}}=10.9760$
连杆上的一点 $P$ 在Frenet标架 ${R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}$ 中的极坐标为 $(5.7,45∘)(5.7,45{}^\circ )$ ，其在连杆坐标系 ${B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}$ 中的直角坐标为 $(- 1.5518, - 7.2907)$ ，则可由Euler-Savary公式得到 $P$ 点轨迹曲线 $ΓP{{\Gamma }_{P}}$ 在该瞬时对应点处的曲率半径 $ρΓ=3.1285{{\rho }_{\Gamma }}=3.1285$ ，从而可知曲率中心 ${{O}_{P}}$ 在Frenet标架 ${R⃗f;E⃗1f,E⃗2f}\{{{{\vec{R}}}_{f}};{{{\vec{E}}}_{1f}},{{{\vec{E}}}_{2f}}\}$ 中的极坐标为（ $rOP=2.5715,αOP=45∘{{r}_{{{O}_{P}}}}=2.5715,{{\alpha }_{{{O}_{P}}}}=\text{45}{}^\circ$ ），以及在固定坐标系 ${A;i⃗f,j⃗f}\{A;{{{\vec{i}}}_{f}},{{{\vec{j}}}_{f}}\}$ 中的直角坐标为 $(3.5954, - 3.9686)$ 。此时，拐点 ${{P}_{I}}$ 在Frenet标架 ${R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}$ 中的极坐标为 $(4.6853，225∘)(4.6853，225{}^\circ )$ ，在连杆坐标系 ${B;i⃗m,j⃗m}\{B;{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}$ 中的直角坐标为 $(2.4131 ， 2.3080)$ 。将所有特征点的坐标均转换到固定坐标系中描述，结果如下图所示。

1.2.4 高阶曲率理论

平面曲线在一点的曲率只能反映该曲线在该点邻近三个无限接近位置处的几何性质。因而，为获得曲线在该点更大邻域内的几何性质，需要对曲率的高阶导数进行研究。例如，当连杆点的轨迹在某点曲率的一阶导数为特定的值（如零），表明轨迹曲线具有特定的几何意义，在机构学上研究这些点的位置，对机构的分析和综合具有重要的指导意义。
将 $kΓ=r+sin⁡α/k∗r2{{k}_{\Gamma }}=\frac{r+\sin \alpha /k*}{{{r}^{2}}}$ 对弧长参数 $σ\sigma$ 分别进行一次求导以及二次求导可得到∶
$dkΓdσ=1H(1Msin⁡α+1Ncos⁡α−1r)\frac{d{{k}_{\Gamma }}}{d\sigma }=\frac{1}{H}(\frac{1}{M\sin \alpha }+\frac{1}{N\cos \alpha }-\frac{1}{r})$
$d2kΓdσ2=(T−1HdHdσ)dk∗dσ−Hcos⁡α(dk∗dσ)2+1HRQ\frac{{{d}^{2}}{{k}_{\Gamma }}}{d{{\sigma }^{2}}}=(T-\frac{1}{H}\frac{dH}{d\sigma })\frac{dk*}{d\sigma }-H\cos \alpha {{(\frac{dk*}{d\sigma })}^{2}}+\frac{1}{H}RQ$
式中：
${1H=−3sin⁡αcos⁡αr2k∗,1M=km−k∗3,1N=13k∗dk∗dσ,T=3Mcot⁡α+1N(2−tan⁡2α)R=1N2cos⁡αsin⁡2α,Q=tan⁡4α+c1tan⁡3α+c2tan⁡2α+c3tan⁡α+c4c1=−kmN+NM,c2=−(1+dNdσ),c3=NM2(dMdσN+3M),c3=(Mkm−2)N2M2\left\{ \begin{matrix} \frac{1}{H}=-\frac{3\sin \alpha \cos \alpha }{{{r}^{2}}k*},\frac{1}{M}=\frac{{{k}_{m}}-k*}{3},\frac{1}{N}=\frac{1}{3k*}\frac{dk*}{d\sigma },T=\frac{3}{M}\cot \alpha +\frac{1}{N}(2-{{\tan }^{2}}\alpha ) \\ R=\frac{1}{{{N}^{2}}}\frac{\cos \alpha }{{{\sin }^{2}}\alpha },Q={{\tan }^{4}}\alpha +{{c}_{1}}{{\tan }^{3}}\alpha +{{c}_{2}}{{\tan }^{2}}\alpha +{{c}_{3}}\tan \alpha +{{c}_{4}} \\ {{c}_{1}}=-{{k}_{m}}N+\frac{N}{M},{{c}_{2}}=-(1+\frac{dN}{d\sigma }),{{c}_{3}}=\frac{N}{{{M}^{2}}}(\frac{dM}{d\sigma }N+3M),{{c}_{3}}=\frac{(M{{k}_{m}}-2){{N}^{2}}}{{{M}^{2}}} \\ \end{matrix} \right.$

详细推导：
已知： $drdσ=−cos⁡α,dαdσ=−km+sin⁡αr,kΓ=1r+sin⁡αr2k∗\frac{dr}{d\sigma }=-\cos \alpha ,\frac{d\alpha }{d\sigma }=-{{k}_{m}}+\frac{\sin \alpha }{r},{{k}_{\Gamma }}=\frac{1}{r}+\frac{\sin \alpha }{{{r}^{2}}k*}$
${dkΓdσ=cos⁡αr2+cos⁡αdαdσr2k∗−sin⁡α(2rdrdσk∗+r2dk∗dσ)r4k∗2=cos⁡αr2+cos⁡α(−km+sin⁡αr)rk∗−sin⁡α(−2cos⁡αk∗+rdk∗dσ)r3k∗2=cos⁡αr2+−rk∗kmcos⁡α+sin⁡αcos⁡αk∗+2sin⁡αcos⁡αk∗−rsin⁡αdk∗dσ)r3k∗2=rk∗2cos⁡α−rk∗kmcos⁡α+3sin⁡αcos⁡αk∗−rsin⁡αdk∗dσ)r3k∗2=−3sin⁡αcos⁡αr2k∗(rk∗km3sin⁡α−rk∗23sin⁡α−k∗+rdk∗dσ3cos⁡αrk∗)=1H(1Msin⁡α+1Ncos⁡α−1r)\left\{ \begin{matrix} \frac{d{{k}_{\Gamma }}}{d\sigma }=\frac{\cos \alpha }{{{r}^{2}}}+\frac{\cos \alpha \frac{d\alpha }{d\sigma }{{r}^{2}}k*-\sin \alpha (2r\frac{dr}{d\sigma }k*+{{r}^{2}}\frac{dk*}{d\sigma })}{{{r}^{4}}k{{*}^{2}}} \\ =\frac{\cos \alpha }{{{r}^{2}}}+\frac{\cos \alpha (-{{k}_{m}}+\frac{\sin \alpha }{r})rk*-\sin \alpha (-2\cos \alpha k*+r\frac{dk*}{d\sigma })}{{{r}^{3}}k{{*}^{2}}} \\ =\frac{\cos \alpha }{{{r}^{2}}}+\frac{-rk*{{k}_{m}}\cos \alpha +\sin \alpha \cos \alpha k*+2\sin \alpha \cos \alpha k*-r\sin \alpha \frac{dk*}{d\sigma })}{{{r}^{3}}k{{*}^{2}}} \\ \begin{matrix} =\frac{rk{{*}^{2}}\cos \alpha -rk*{{k}_{m}}\cos \alpha +3\sin \alpha \cos \alpha k*-r\sin \alpha \frac{dk*}{d\sigma })}{{{r}^{3}}k{{*}^{2}}} \\ =-\frac{3\sin \alpha \cos \alpha }{{{r}^{2}}k*}(\frac{\frac{rk*{{k}_{m}}}{3\sin \alpha }-\frac{rk{{*}^{2}}}{3\sin \alpha }-k*+\frac{r\frac{dk*}{d\sigma }}{3\cos \alpha }}{rk*}) \\ =\frac{1}{H}(\frac{1}{M\sin \alpha }+\frac{1}{N\cos \alpha }-\frac{1}{r}) \\ \end{matrix} \\ \end{matrix} \right.$

（1）曲率驻点 当运动刚体 $Σ*\Sigma \text{*}$ 上点 $P$ 轨迹曲线 $ΓP{{\Gamma }_{\text{P}}}$ 的曲率 $kΓ{{k}_{\Gamma }}$ 对弧长参数 $σ\sigma$ 的一阶导数为零时，表示该点轨迹此时曲率变化率为零，称其为曲率驻点。令式（1.76）为零，可化简得∶
$1r=1Msin⁡α+1Nsin⁡α\frac{1}{r}=\frac{1}{M\sin \alpha }+\frac{1}{N\sin \alpha }$
上式在瞬心线的Frenet标架 ${R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}$ 中描述，可通过Frenet标架到运动坐标系 ${O⃗m;i⃗m,j⃗m}\{{{{\vec{O}}}_{m}};{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}$ 的坐标变换将其转换到运动坐标系中描述，可得到关于点坐标 ${{x}_{Pm}},{{y}_{Pm}})$ 的三次代数方程。将满足该方程的曲线称为刚体平面上的曲率驻点曲线，刚体上满足曲率驻点条件的点都分布在这条曲线上。曲率驻点无限接近四个位置均在一圆上，或者说其轨迹曲线在该点处与圆三阶接触。随着刚体的运动（对所有时刻 $σ\sigma$ ）刚体平面上的曲率驻点曲线形成曲线族。
（2）Ball点 当运动刚体 $Σ*\Sigma \text{*}$ 上点的轨迹曲线的曲率 $kΓ{{k}_{\Gamma }}$ 及其一阶导数 $dkΓ/dσd{{k}_{\Gamma }}/d\sigma$ 同时为零，即式（1.75）与式（1.79）联立，得到该点在Frenet标架 ${R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}$ 中极坐标 $(r,α)(r,\alpha )$ 满足的方程为∶
${tan⁡α=k∗(km+2k∗)dk∗/dσr=−sin⁡αk∗\left\{ \begin{matrix} \tan \alpha =\frac{k*({{k}_{m}}+2k*)}{dk*/d\sigma } \\ r=-\frac{\sin \alpha }{k*} \\ \end{matrix} \right.$
该点为拐点圆与曲率驻点曲线的交点，称为Ball点。由1.1.2节可知，平面运动刚体上Ball 点的轨迹曲线在该点的四个无限接近位置共一直线，或与直线三阶接触。
（3）Burmester点 当运动刚体 $Σ*\Sigma \text{*}$ 上点的轨迹曲线的曲率一阶导数 $dkΓ/dσd{{k}_{\Gamma }}/d\sigma$ 、二阶导数 $d2kΓ/dσ2{{d}^{2}}{{k}_{\Gamma }}/d{{\sigma }^{2}}$ 同时为零，则由式（1.76）和式（1.77）得到该点在Frenet标架 ${R⃗m;E⃗1m,E⃗2m}\{{{{\vec{R}}}_{m}};{{{\vec{E}}}_{1m}},{{{\vec{E}}}_{2m}}\}$ 中极坐标 $(r,α)(r,\alpha )$ 满足的方程为∶
${1r=1Msin⁡α+1Nsin⁡αtan⁡4α+c1tan⁡3α+c2tan⁡2α+c3tan⁡α+c4=0\left\{ \begin{matrix} \frac{1}{r}=\frac{1}{M\sin \alpha }+\frac{1}{N\sin \alpha } \\ {{\tan }^{4}}\alpha +{{c}_{1}}{{\tan }^{3}}\alpha +{{c}_{2}}{{\tan }^{2}}\alpha +{{c}_{3}}\tan \alpha +{{c}_{4}}=0 \\ \end{matrix} \right.$
式（1.81）中的第二式为 $tan⁡α\tan \alpha$ 的四次方程，最多有四个实数解。将满足该方程式的刚体平面上的点称为 Burmester 点，其在固定坐标系中的轨迹曲线在该点处的曲率同时满足 $dkΓ/dσ=0d{{k}_{\Gamma }}/d\sigma=0$ 和 $d2kΓ/dσ2=0{{d}^{2}}{{k}_{\Gamma }}/d{{\sigma }^{2}}=0$ 。这表明轨迹曲线在该点的无限接近五位置均在一圆上，或者说轨迹曲线在该点与圆四阶接触。

Burmester点的推导单独令写文章进行推导，（待补充）

（4）Ball点曲线及其奇点 由式（1.80）可以得到每一瞬时（瞬心线弧长 $σ\sigma$ 处）运动刚体 $Σ*\Sigma \text{*}$ 上的一个 Ball点，当刚体经过平面运动后，运动刚体上在不同瞬时的 Ball 点集合就组成了运动刚体上的Ball点曲线，Ball点在Frenet标架中的坐标 $(r,α)(r,\alpha )$ 或者运动坐标系中的坐标 ${{x}_{Pm}},{{y}_{Pm}}$ ]则为瞬心线弧长参数σ的函数，并满足式（1.80）。
对于刚体平面上运动坐标系 ${O⃗m;i⃗m,j⃗m}\{{{{\vec{O}}}_{m}};{{{\vec{i}}}_{m}},{{{\vec{j}}}_{m}}\}$ 中的一点 $P({{x}_{Pm}},{{y}_{Pm}})$ ，其轨迹曲线的曲率如式（1.74c）所描述∶
$kΓ=F(xPm,yPm,s)G(xPm,yPm,s){{k}_{\Gamma }}=\frac{F({{x}_{Pm}},{{y}_{Pm}},s)}{G({{x}_{Pm}},{{y}_{Pm}},s)}$
式中， $s$ 为原曲线 $ΓOm{{\Gamma }_{Om}}$ 的弧长， $F$ 和 $G$ 为刚体上点坐标 ${{x}_{Pm}},{{y}_{Pm}})$ 以及弧长 $s$ 的函数，如式（1.74c）所示。
将上式对弧长参数 $s$ 求导，并且令 $dkΓds=0\frac{d{{k}_{\Gamma }}}{ds}=0$ ，可得到：
$dkΓds=1G(dFdsG−dGdsF)=0\frac{d{{k}_{\Gamma }}}{ds}=\frac{1}{G}(\frac{dF}{ds}G-\frac{dG}{ds}F)=0$
由上式同样可以得到如式（1.79）关于刚体上点坐标的三次代数方程。令式（1.82）为零，并结合上式可得到Ball点满足的条件式∶
$F(xPm,yPm,s)=0,∂F∂s=0F({{x}_{Pm}},{{y}_{Pm}},s)=0,\frac{\partial F}{\partial s}=0$
对于原曲线 $ΓOm{{\Gamma }_{Om}}$ 弧长参数 $s$ 的一段区间，上式的前一式描述了刚体平面上的一组拐点圆，而后一式则为将拐点圆位置对弧长参数 $s$ 求导，由于 $F$ 为 ${{x}_{Pm}},{{y}_{Pm}})$ 和 $s$ 的函数，因而上式描述了该组拐点圆的包络线。
将式（1.74c）中 $F$ 的表达式代入式（1.84），可得到两组解，其中一组为：
${xm=u1(1)cos⁡θ−u2(1)sin⁡θym=u1(1)sin⁡θ+u2(1)cos⁡θ\left\{ \begin{matrix} {{x}_{m}}={{u}_{1}}^{(1)}\cos \theta -{{u}_{2}}^{(1)}\sin \theta \\ {{y}_{m}}={{u}_{1}}^{(1)}\sin \theta +{{u}_{2}}^{(1)}\cos \theta \\ \end{matrix} \right.$
其中： $u1(1)=0;u2(1)=1kOm−θ˙{{u}_{1}}^{(1)}=0;{{u}_{2}}^{(1)}=\frac{1}{{{k}_{Om}}-\dot{\theta }}$
另一组解为：
${xm=u1(2)cos⁡θ−u2(2)sin⁡θym=u1(2)sin⁡θ+u2(2)cos⁡θ\left\{ \begin{matrix} {{x}_{m}}={{u}_{1}}^{(2)}\cos \theta -{{u}_{2}}^{(2)}\sin \theta \\ {{y}_{m}}={{u}_{1}}^{(2)}\sin \theta +{{u}_{2}}^{(2)}\cos \theta \\ \end{matrix} \right.$
其中：
${u1(2)=Cθ˙(kOm−θ˙)−C2(k˙Om−θ¨)(1+C2)(kOm−θ˙)3u2(2)=1kOm−θ˙+Cθ˙(kOm−θ˙)+C2(k˙Om−θ¨)(1+C2)(kOm−θ˙)3C=θ˙(kOm−θ˙)2(k˙Om−θ¨)+θ˙2(kOm−θ˙)3(2kOm−θ˙)+(kOm−θ˙)2(k˙Om−θ¨)(2k˙Om−3θ¨)θ˙θ¨(kOm−θ˙)3+(kOm−θ˙)(k˙Om−θ¨)(k¨Om−dθ¨/ds)−2θ˙2(k˙Om−θ¨)(kOm−θ˙)2−3(k˙Om−θ¨)3\left\{ \begin{matrix} {{u}_{1}}^{(2)}=\frac{C\dot{\theta }({{k}_{Om}}-\dot{\theta })-{{C}^{2}}({{{\dot{k}}}_{Om}}-\ddot{\theta })}{(1+{{C}^{2}}){{({{k}_{Om}}-\dot{\theta })}^{3}}} \\ {{u}_{2}}^{(2)}=\frac{1}{{{k}_{Om}}-\dot{\theta }}+\frac{C\dot{\theta }({{k}_{Om}}-\dot{\theta })+{{C}^{2}}({{{\dot{k}}}_{Om}}-\ddot{\theta })}{(1+{{C}^{2}}){{({{k}_{Om}}-\dot{\theta })}^{3}}} \\ C=\frac{\dot{\theta }{{({{k}_{Om}}-\dot{\theta })}^{2}}({{{\dot{k}}}_{Om}}-\ddot{\theta })+{{{\dot{\theta }}}^{2}}{{({{k}_{Om}}-\dot{\theta })}^{3}}(2{{k}_{Om}}-\dot{\theta })+{{({{k}_{Om}}-\dot{\theta })}^{2}}({{{\dot{k}}}_{Om}}-\ddot{\theta })(2{{{\dot{k}}}_{Om}}-3\ddot{\theta })}{\dot{\theta }\ddot{\theta }{{({{k}_{Om}}-\dot{\theta })}^{3}}+({{k}_{Om}}-\dot{\theta })({{{\dot{k}}}_{Om}}-\ddot{\theta })({{{\ddot{k}}}_{Om}}-d\ddot{\theta }/ds)-2{{{\dot{\theta }}}^{2}}({{{\dot{k}}}_{Om}}-\ddot{\theta }){{({{k}_{Om}}-\dot{\theta })}^{2}}-3{{({{{\dot{k}}}_{Om}}-\ddot{\theta })}^{3}}} \\ \end{matrix} \right.$

式（1.85）和式（1.86）描述了拐点圆族的两条包络线。式（1.85）同1.2.1节中的式（1.42），描述了刚体平面上的动瞬心线；式（1.86）则为Ball点曲线的另一种表达形式。注意这两条包络线并不是等距线，因为拐点圆的半径随拐点圆位置不同而变化。
对于刚体平面上Ball点曲线的几何性质进行讨论，式（1.84）给出了Ball点满足的条件，而式（1.86a）则给出了Ball点的具体位置方程，可以将其写为∶
${{x}_{bm}}={{x}_{bm}}(s),{{y}_{bm}}={{y}_{bm}}(s)$
如果某一瞬时Ball点曲线上出现奇点，则：
$x˙bm=dxbmds=0,y˙bm=dybmds=0{{{\dot{x}}}_{bm}}=\frac{d{{x}_{bm}}}{ds}=0,{{{\dot{y}}}_{bm}}=\frac{d{{y}_{bm}}}{ds}=0$
将式（1.84）的的隐函数对弧长参数 $s$ 求偏导，可得∶
${Fxbmx˙bm+Fybmy˙bm+Fs=0Fxxbmx˙bm+Fxybmy˙bm+Fss=0\left\{ \begin{matrix} {{F}_{{{x}_{bm}}}}{{{\dot{x}}}_{bm}}+{{F}_{{{y}_{bm}}}}{{{\dot{y}}}_{bm}}+{{F}_{s}}=0 \\ {{F}_{x{{x}_{bm}}}}{{{\dot{x}}}_{bm}}+{{F}_{x{{y}_{bm}}}}{{{\dot{y}}}_{bm}}+{{F}_{ss}}=0 \\ \end{matrix} \right.$