表现良好的最长时段[前缀和思想子数组]
前缀和与最长子数组
- 前言
- 一、表现良好的最长时间段
- 二、前缀和思想&子数组
- 1、前缀和&map
- 2、前缀和&单调栈
- 总结
- 参考文献
前言
对于子数组/子串问题,紧密连续前缀和/滑动窗口/单调栈;挖掘内在规律,可以简化代码,降低时空复杂度或消耗量。
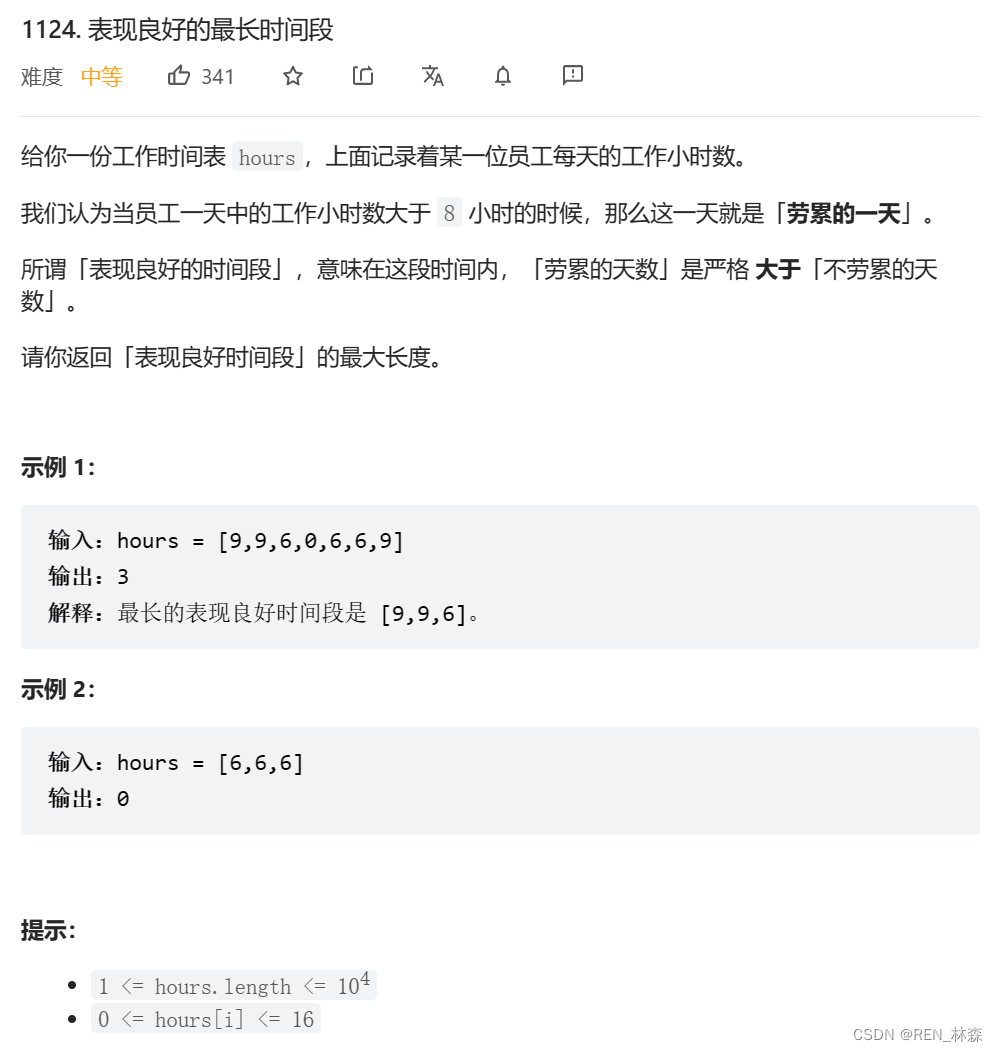
一、表现良好的最长时间段
二、前缀和思想&子数组
1、前缀和&map
抽象一下工作时长,工作时长不重要,重要的是两种类型,用1/-1标记两种类型,问题就转换成了求和为正数的最长子数组。
采用前缀和思想,用map记录前面前缀和,重复的只记最前面(为了最长子数组),为了让和为正数,当sum < 0时,查阅map中是否存在(sum - 1)即可。
class Solution {public int longestWPI(int[] hours) {// 由于只有1和-1,不可能前缀和出现跳跃的情况,所有hashMap就可以处理。// TreeMap<Integer,Integer> tm = new TreeMap<>();Map<Integer,Integer> fx = new HashMap<>();for(int i = 0;i < hours.length;i++){hours[i] = hours[i] > 8 ? 1:-1;}int sum = 0;int max = 0;for(int i = 0;i < hours.length;i++){sum += hours[i];// 记录最大长度if(sum > 0) max = i + 1;else if(fx.containsKey(sum - 1)){max = Math.max(max,-fx.get(sum - 1) + i);}// 为了最长子数组,只记录最前面的前缀和。if(!fx.containsKey(sum)) fx.put(sum,i);}return max;}
}
// 总结:对于连续子数组问题,多半前缀和/滑动窗口/单调栈
// 1-如何确定连续时间段?两层for循环暴力确定?以结果向导的前缀和确定!!!
// 2-如何确定该连续时间段有效?根据map中记录的前缀和确定。
2、前缀和&单调栈
前缀和子数组[l , r]有如下特点,
当prfix[r] > prefix[l]时,则该子数组是有效数组,当prefix[l1] < prefix[l2],那么l2作为左边界是无意义的,毕竟l2可以,则l1也可以,而且还更长,所以记录一下单调减序列即可。
注:这里的单调栈和传统的单调栈不同,不是整个数组的单调栈,没有出栈操作。
再反向遍历前缀和数组,和栈中元素比较,不断出栈寻找prefix[r] > min(prefix[l]),再记录最长数组长度。
这里出栈元素是对接下来的r没有影响的,证明如下,
当r1 > r 2时,则l1 > l2,两个数组存在包含关系,没有影响。
当r1 < r2时,则l1 < l2,按照单调栈规则,l1一定在l2上面,所以出栈l1是没任何影响的。
// 单调栈
func longestWPI(hours []int) int {// 问题转换,求和大于0的最长子数组;updateHours(hours)// 记录前缀和prefix := recordPrefix(hours)// 得到单调减栈stack,top := getStack(prefix)//fmt.Println(prefix)//fmt.Println(stack)// 寻找最大子数组i := len(prefix) - 1m := 0for ; i > 0;i-- {// 剪枝,一旦prefix>0,即前面的子数组最大良好就是本身。if prefix[i] > 0 {return max(m,i)}k := ifor ; top > 0 && prefix[stack[top - 1]] < prefix[i] ; {top--k = stack[top]}m = max(m,i - k)}return m
}
func getStack(prefix []int)([]int,int){stack := make([]int,0)top := 0for i := 1;i < len(prefix);i++ {if top == 0 || prefix[stack[top - 1]] > prefix[i] {stack = append(stack[:top],i)top++} }return stack,top
}
func recordPrefix(hours []int)[]int{prefix := make([]int,len(hours) + 1)for i,h := range hours {prefix[i + 1] = prefix[i] + h }return prefix
}
func updateHours(hours []int) {for i := 0;i < len(hours);i++ {if hours[i] > 8 {hours[i] = 1}else {hours[i] = -1}}
}
func max(x,y int) int {if x > y {return x}return y
}
总结
1)对于子数组/子串问题,紧密连续前缀和/滑动窗口/单调栈。
2)挖掘内在规律,可以简化代码,降低时空复杂度或消耗量。比如这里单调栈,将前缀和简化;比如这里不用TreeMap排序,数值只有1/0/-1三种可能,前缀和必定连续。
参考文献
[1] LeetCode 表现良好的最长时段
[2] LeetCode 官方题解
