回溯算法章末总结
-
组合问题的特点
(1)ab=ba 选中a之后,就不再选了
(2)找出所有的组合 (长度可以不相等) -
组合问题模板

-
做回溯题步骤
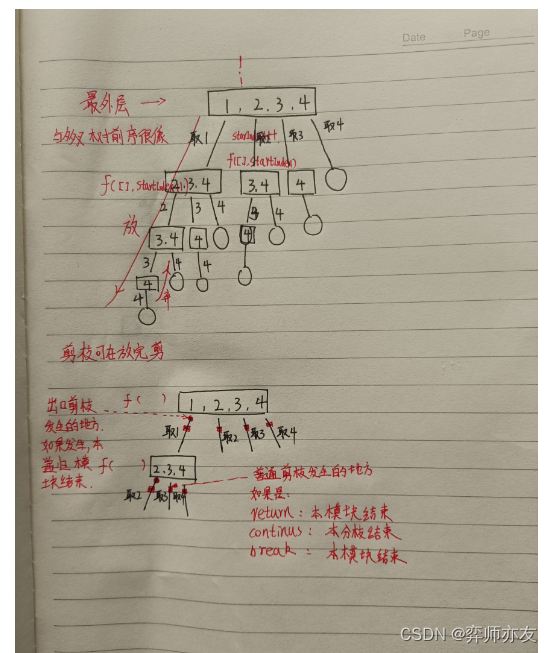
(0)判断问题类型
(1)树状图
(2)递归三部曲
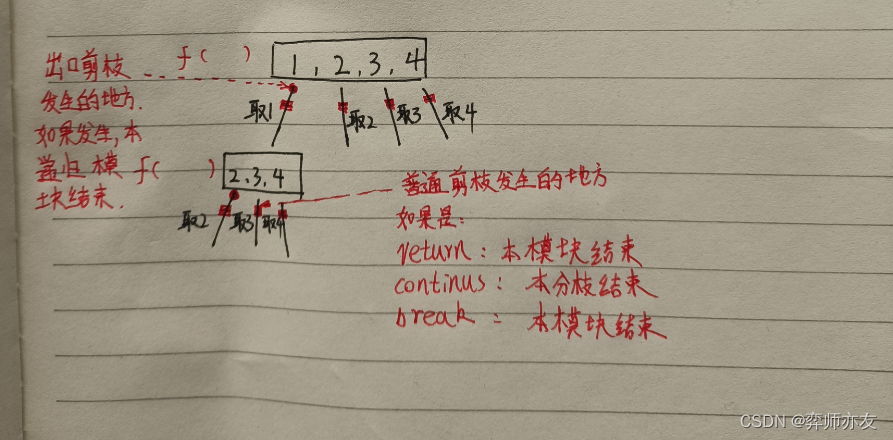
(3)剪枝条件 -
组合问题中的纵横剪枝 ----> 216.组合总和III
-
去重
(1)横向去重
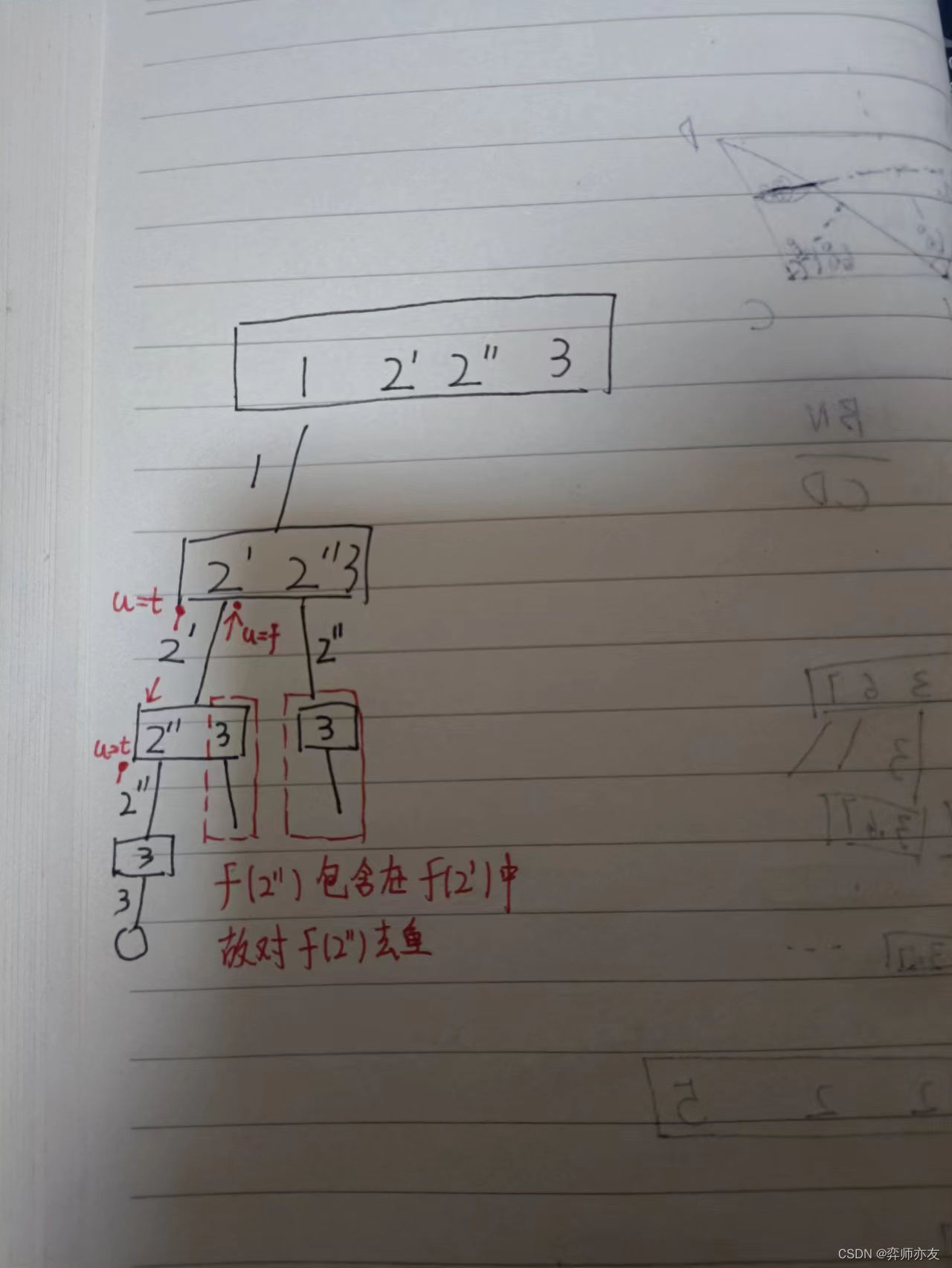
(2)set横向去重
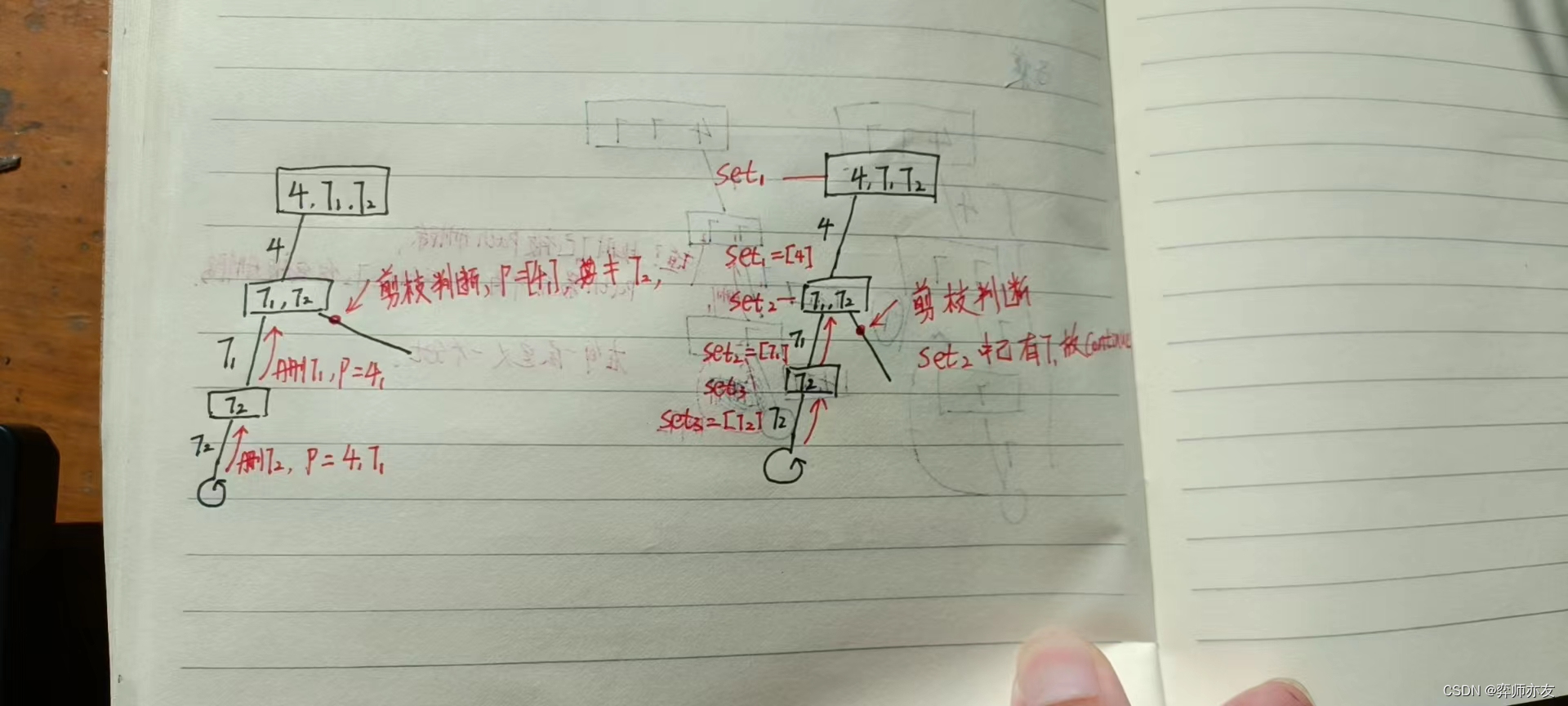
代码
public void findSubsequencesBT(int[] nums,int startIndex) {HashSet<Integer> set = new HashSet<>();for (int i = startIndex; i < nums.length; i++) {// 剪枝if (findSubsequencesPath.size()>0&&findSubsequencesPath.get(findSubsequencesPath.size()-1)[0]>nums[i]){continue;}// 此处不能是==,只能是>= 为空时也要判断去重if ((findSubsequencesPath.size()==0||findSubsequencesPath.size()>0&&findSubsequencesPath.get(findSubsequencesPath.size()-1)[0]<=nums[i])&&set.contains(nums[i])){continue;}//三件套//using[i]=true;findSubsequencesPath.add(new int[]{nums[i],i});set.add(nums[i]);if (findSubsequencesPath.size()>=2){ArrayList<Integer> temp = new ArrayList<>();for (int j = 0; j <findSubsequencesPath.size() ; j++) {temp.add(findSubsequencesPath.get(j)[0]);}ires.add(temp);}findSubsequencesBT(nums,i+1);findSubsequencesPath.remove(findSubsequencesPath.size()-1);// set 不用回溯,每层一个// using[i]=false;}}
关键
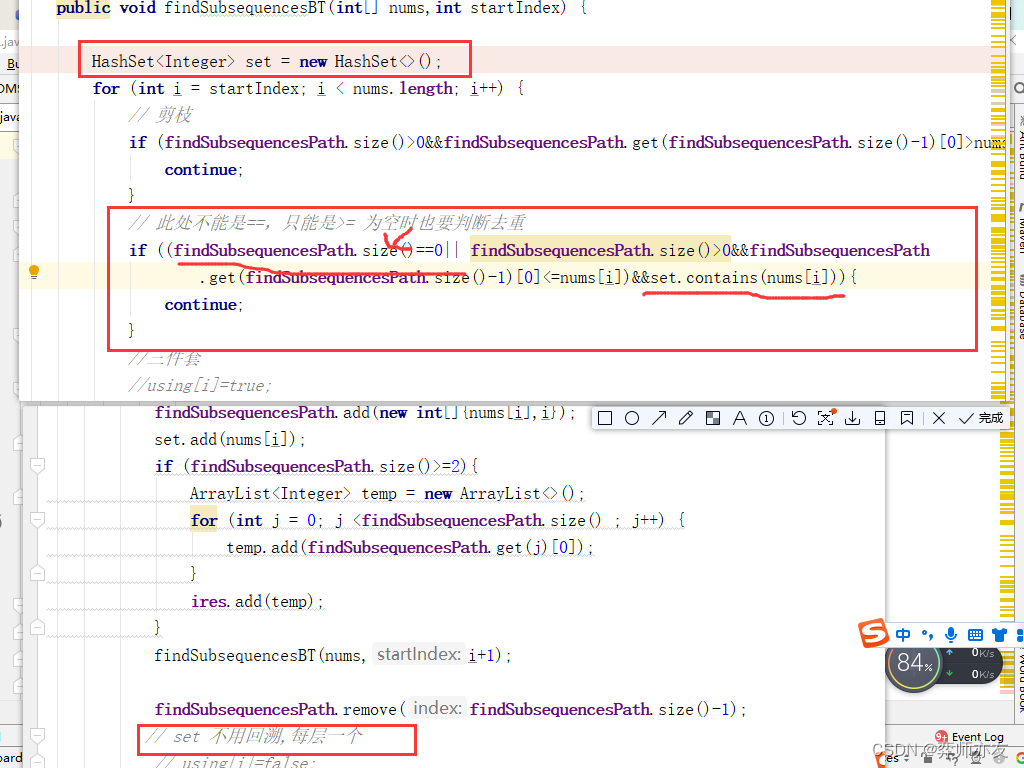
- 分割递归终止条件
分割常用的递归出口
(1)startIndex==数组长度
缺点: 如果是分割有段数要求,例如ip,可能分割很多段后才到递归出口,1.1.1.1.1.1.1 再判断,白白浪费性能。
改进:当已经分割三段时,第四段直接判断,这样可以剪掉部分,但是最后还是会一个一个试
public void restoreIpAddressesBT(String s,int startIndex) {if (startIndex==s.length()){if (restoreIpAddressesPath.size()==4){StringBuilder sb = new StringBuilder();for (String s1 : restoreIpAddressesPath) {sb.append(s1+".");}sb.delete(sb.length()-1,sb.length());slist.add(sb.toString());}return;}for (int i = startIndex; i <s.length() ; i++) {String substring = s.substring(startIndex, i + 1);// 剪枝// 如果已经有3个了,直接看剩下的能不能凑成第四个就行if (restoreIpAddressesPath.size()==3&&valIsValid(s.substring(startIndex))==-1){return; // 本层全不能用}if (valIsValid(substring)==-1){continue;}restoreIpAddressesPath.add(substring);restoreIpAddressesBT(s,i+1);restoreIpAddressesPath.remove(restoreIpAddressesPath.size()-1);}}
(2)如果有段数要求,直接用段数作为剪枝条件
if (restoreIpAddressesPath.size()==4){if (startIndex==s.length()){StringBuilder sb = new StringBuilder();for (String s1 : restoreIpAddressesPath) {sb.append(s1+".");}sb.delete(sb.length()-1,sb.length());slist.add(sb.toString());}return;}
这样只要到段数,就会判断,不会再 1.1.1.1.1.1.1这样分
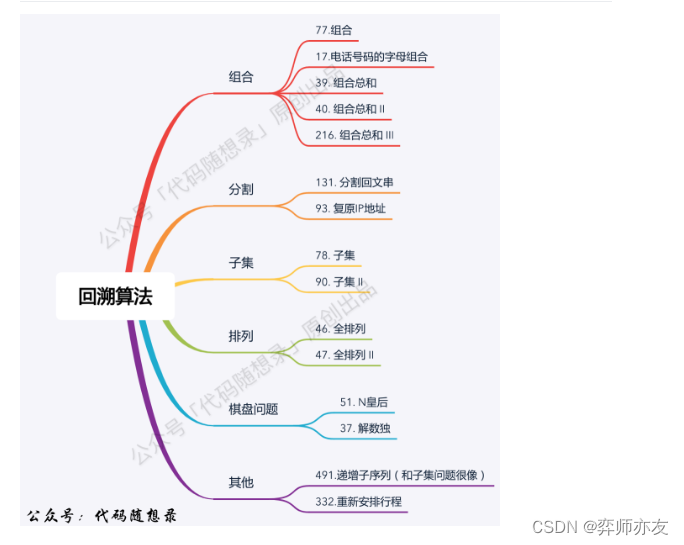
题型
组合问题
每条从根出发的子路径是一个结果
- 传统组合问题 每一条子路径都是一种组合 —>● 77. 组合● 216.组合总和III
- 从筐中取球类型–>● 17.电话号码的字母组合
- 组合,元素不重,元素可重复取 39. 组合总和
- 组合,元素重复,结果不重,横向去重–> 40.组合总和II
子集问题
- 组合问题之子集问题,找到所有从根节点出发的子路径,包含【】
---->78.子集 - 组合问题之递增序列,本质是子集问题,使用set去重,注意第一层时path可能为空 491.递增子序列
分割
每条路径是一个结果
5. 标准分割 --> 131.分割回文串 ● 93.复原IP地址
排列
- 排列,借助used数组 46.全排列 47.全排列 II
递归树
-
传统组合
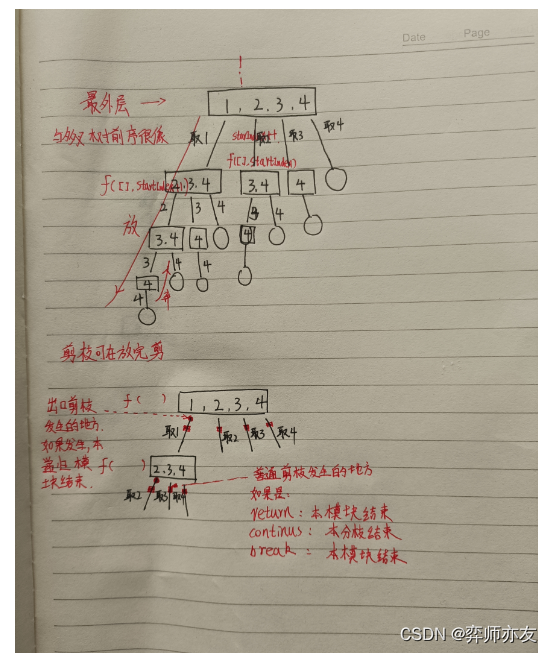
-
筐中取球
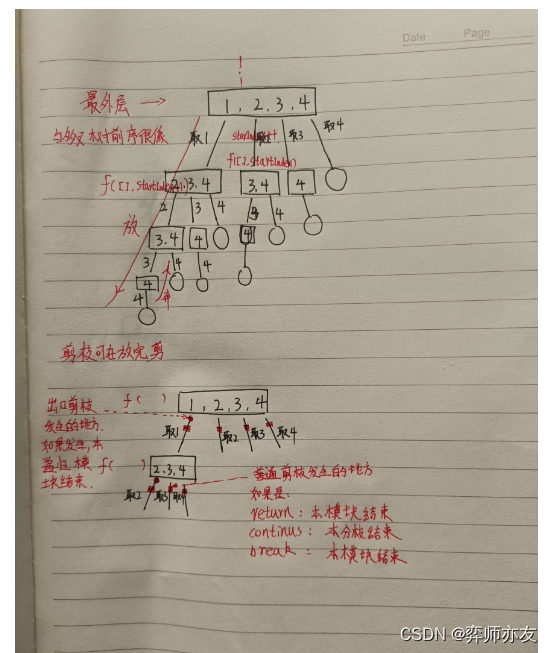
-
组合,每个元素可重复
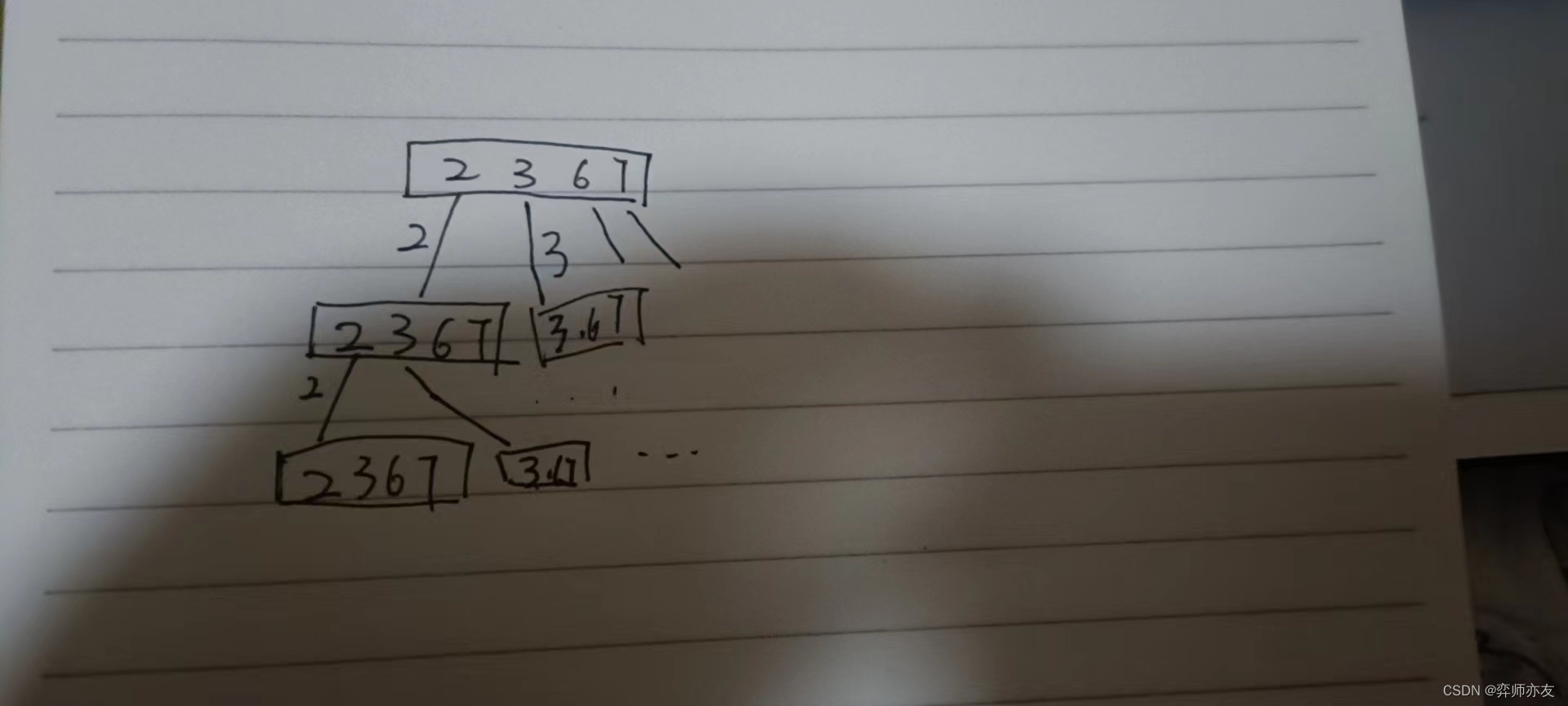
-
组合,元素重复,结果不重,横向去重
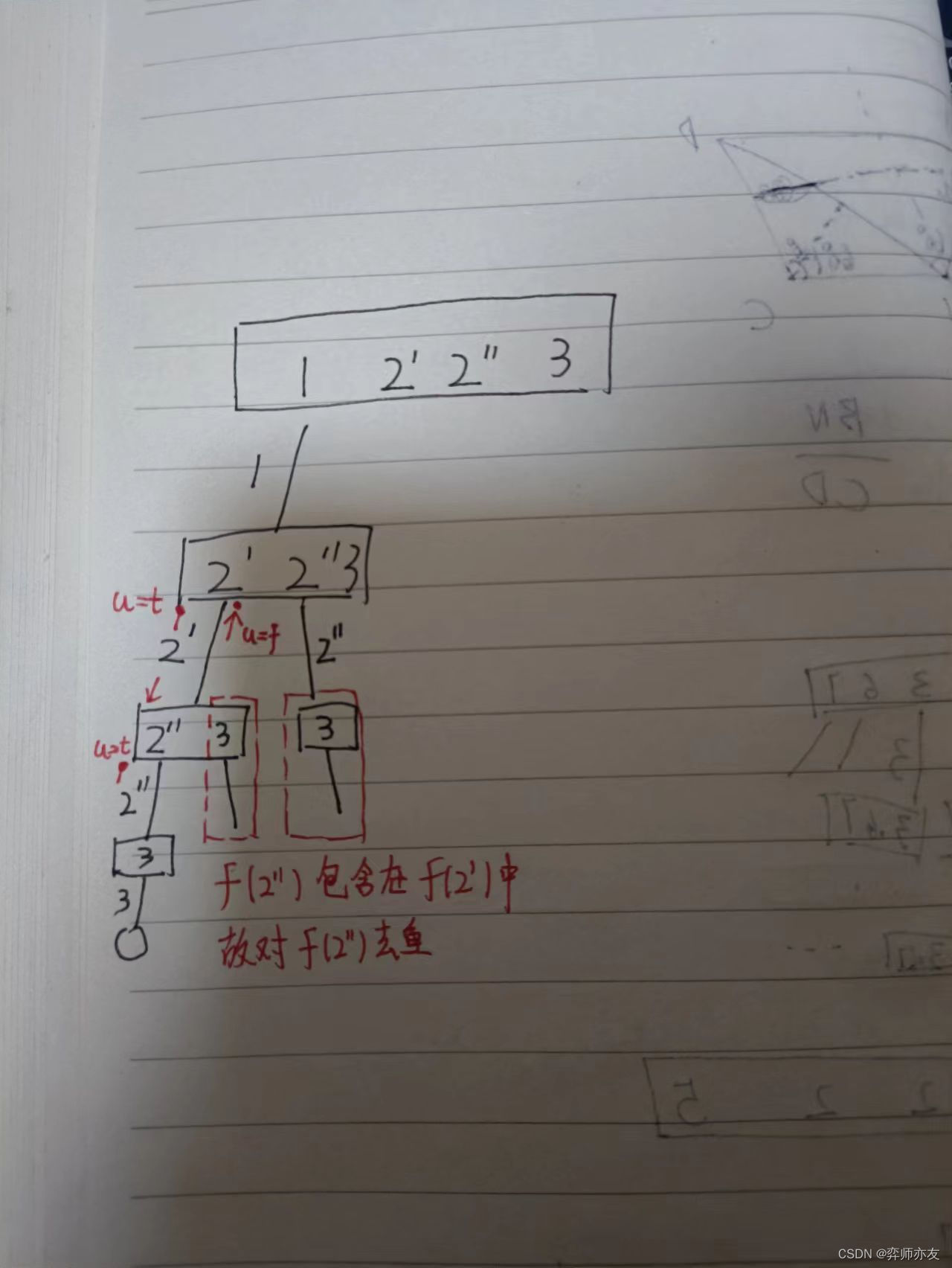
-
标准分割

(2)分割模板
// 131.分割回文串 public void partitionBT(String s,int startIndex) {if (startIndex==s.length()){sres.add(new ArrayList<>(spath));return;}// 引擎for (int i = startIndex; i <s.length() ; i++) {// 剪枝if (!isPalindrome(s,i,startIndex)){return;}spath.add(s.substring(i, startIndex + 1));partitionBT(s,i+1);spath.remove(spath.size()-1);// 本层下一个}}
(3)不同之处

6. 子集问题
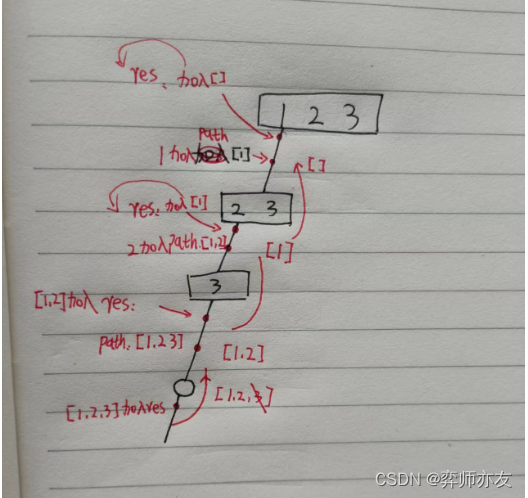
(2)子集问题模板
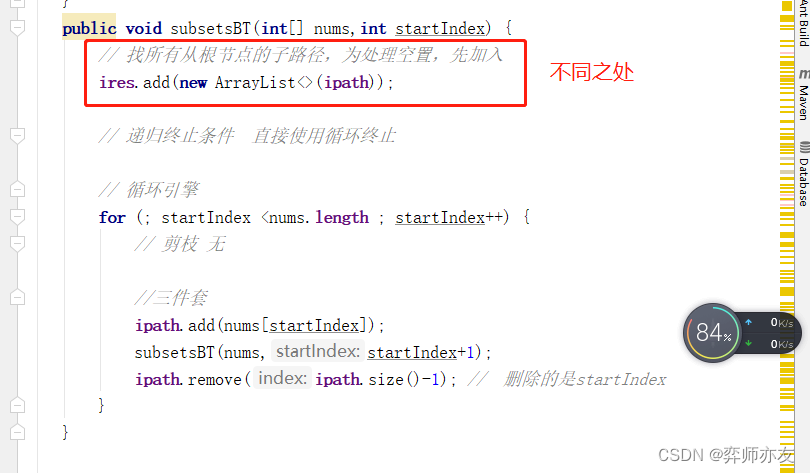
// 78. 子集public void subsetsBT(int[] nums,int startIndex) {// 找所有从根节点的子路径,为处理空置,先加入ires.add(new ArrayList<>(ipath));// 递归终止条件 直接使用循环终止// 循环引擎for (; startIndex <nums.length ; startIndex++) {// 剪枝 无//三件套ipath.add(nums[startIndex]);subsetsBT(nums,startIndex+1);ipath.remove(ipath.size()-1); // 删除的是startIndex}}
(3)不同之处
7. 递增序列问题

代码
public void findSubsequencesBT(int[] nums,int startIndex) {HashSet<Integer> set = new HashSet<>();for (int i = startIndex; i < nums.length; i++) {// 剪枝if (findSubsequencesPath.size()>0&&findSubsequencesPath.get(findSubsequencesPath.size()-1)[0]>nums[i]){continue;}// 此处不能是==,只能是>= 为空时也要判断去重if ((findSubsequencesPath.size()==0||findSubsequencesPath.size()>0&&findSubsequencesPath.get(findSubsequencesPath.size()-1)[0]<=nums[i])&&set.contains(nums[i])){continue;}//三件套//using[i]=true;findSubsequencesPath.add(new int[]{nums[i],i});set.add(nums[i]);if (findSubsequencesPath.size()>=2){ArrayList<Integer> temp = new ArrayList<>();for (int j = 0; j <findSubsequencesPath.size() ; j++) {temp.add(findSubsequencesPath.get(j)[0]);}ires.add(temp);}findSubsequencesBT(nums,i+1);findSubsequencesPath.remove(findSubsequencesPath.size()-1);// set 不用回溯,每层一个// using[i]=false;}}
关键

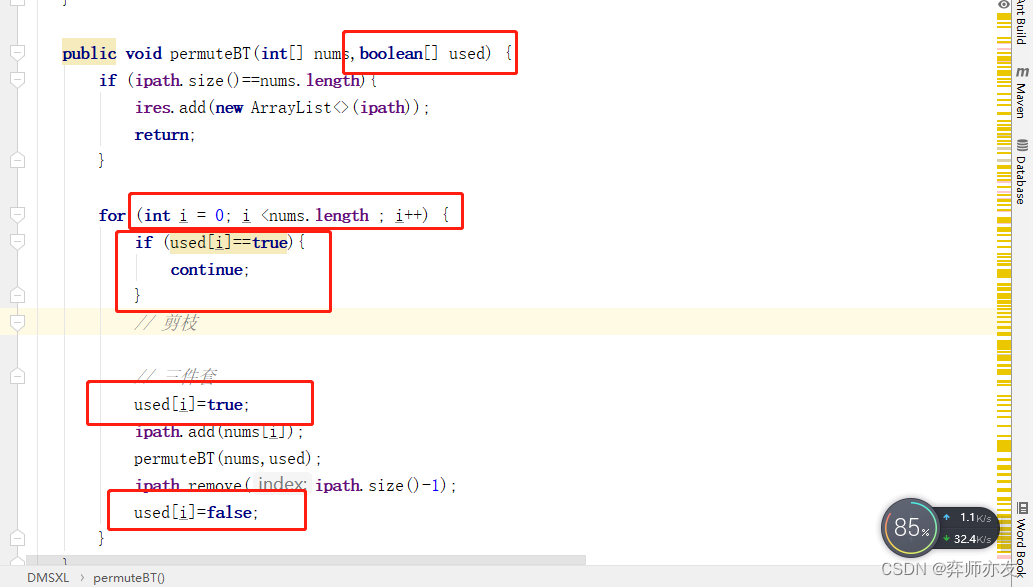
8. 排列
public void permuteBT(int[] nums,boolean[] used) {if (ipath.size()==nums.length){ires.add(new ArrayList<>(ipath));return;}for (int i = 0; i <nums.length ; i++) {if (used[i]==true){continue;}// 剪枝// 三件套used[i]=true;ipath.add(nums[i]);permuteBT(nums,used);ipath.remove(ipath.size()-1);used[i]=false;}}