Leetcode.1124 表现良好的最长时间段
题目链接
Leetcode.1124 表现良好的最长时间段 Rating : 1908
题目描述
我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。
所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格 大于「不劳累的天数」。
请你返回「表现良好时间段」的最大长度。
示例 1:
输入:hours = [9,9,6,0,6,6,9]
输出:3
解释:最长的表现良好时间段是 [9,9,6]。
示例 2:
输入:hours = [6,6,6]
输出:0
提示
- 1<=hours.length<=1041 <= hours.length <= 10^41<=hours.length<=104
- 0<=hours[i]<=160 <= hours[i] <= 160<=hours[i]<=16
分析:
问题转化:工作时间大于8h 看作+1,工作时间 小于等于 8h 看作 -1。所以原问题转化为 求一段连续的区间 [l,r],这个区间和是大于0的,且区间长度最大。
我们用 前缀和 可以在 O(1)O(1)O(1) 的复杂度求出一段连续区间的和。
如果我们暴力枚举 n-1个左端点,寻找最长的区间和sum > 0的区间,会超时…
为此我们使用一个 单调栈 来记录,所有可能的左端点。
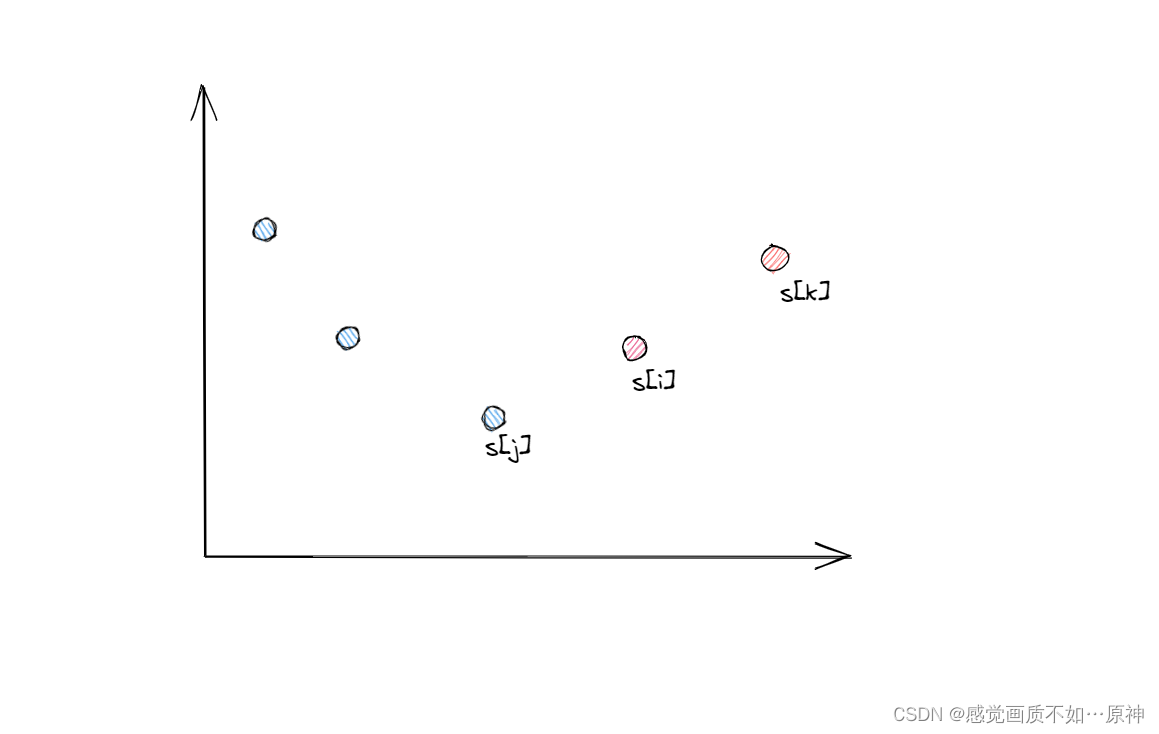
当遍历到 s[i]s[i]s[i] 时,如果 s[j]<s[i]s[j] < s[i]s[j]<s[i],说明 s[j]s[j]s[j] 就可能称为一个左端点。
如果想让 s[i]s[i]s[i] 也有成为左端点的可能,后面必然有一个 s[k]>s[i]s[k] > s[i]s[k]>s[i],但是这样的话 s[k]>s[j]s[k] > s[j]s[k]>s[j],s[i]s[i]s[i] 相比 s[j]s[j]s[j] 更可能成为一个左端点。
所以栈 stk中,要记录的就是这样的点,栈中的元素是从 栈底到栈顶 依次递减的。
最后,我们倒序遍历 前缀和数组s,如果当前的s[i]大于 栈顶元素 s[stk.top()],就更新最大值。
时间复杂度:O(n)O(n)O(n)
代码:
class Solution {
public:int longestWPI(vector<int>& hours) {int n = hours.size();//前缀和数组int s[n+1];s[0] = 0;stack<int> st;//先插入0,处理边界情况st.push(0);for(int i = 1;i <= n;i++){s[i] = s[i-1] + (hours[i-1] > 8 ? 1 : -1);if(s[st.top()] > s[i]) st.push(i);}int ans = 0;for(int i = n;i >= 1;--i){while(!st.empty() && s[i] > s[st.top()]){ans = max(ans , i - st.top());st.pop();}}return ans;}
};
